What Goes On in a Proton? Quark Math Still Conflicts With Experiments.
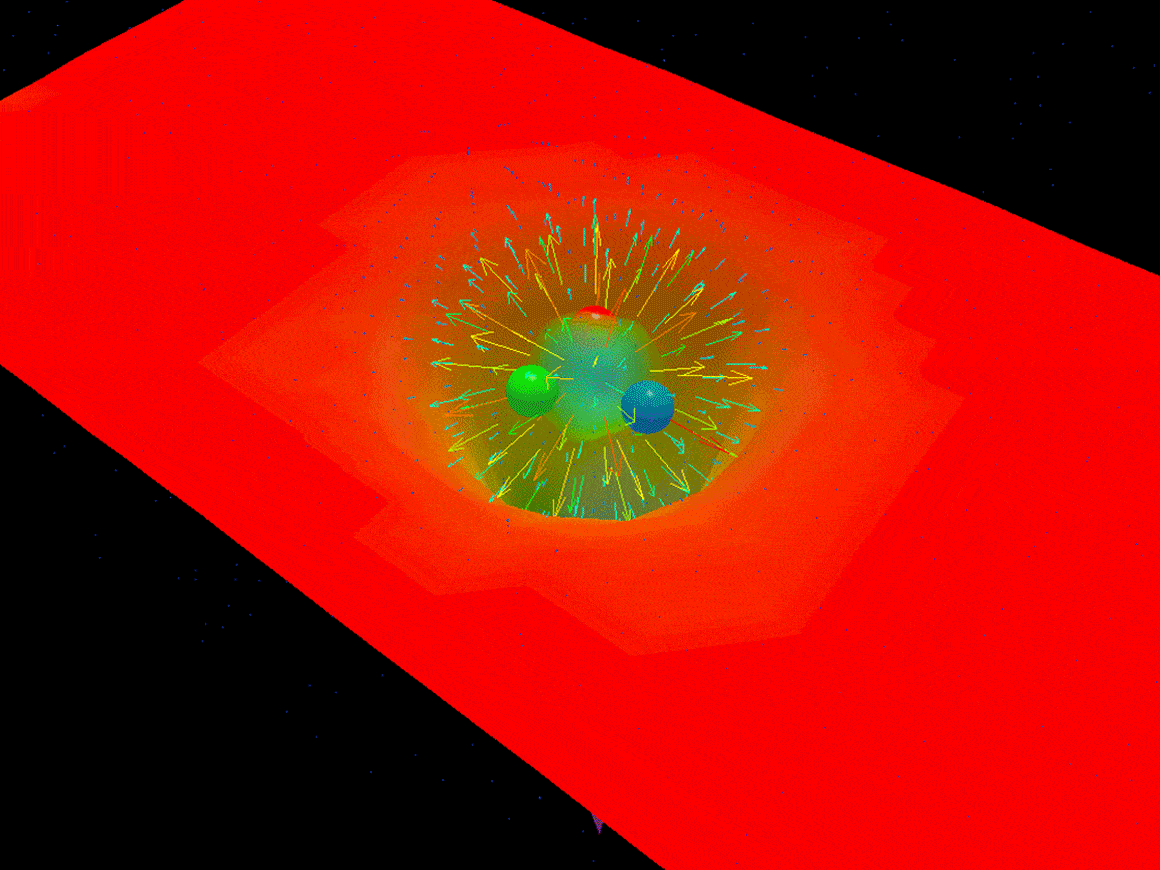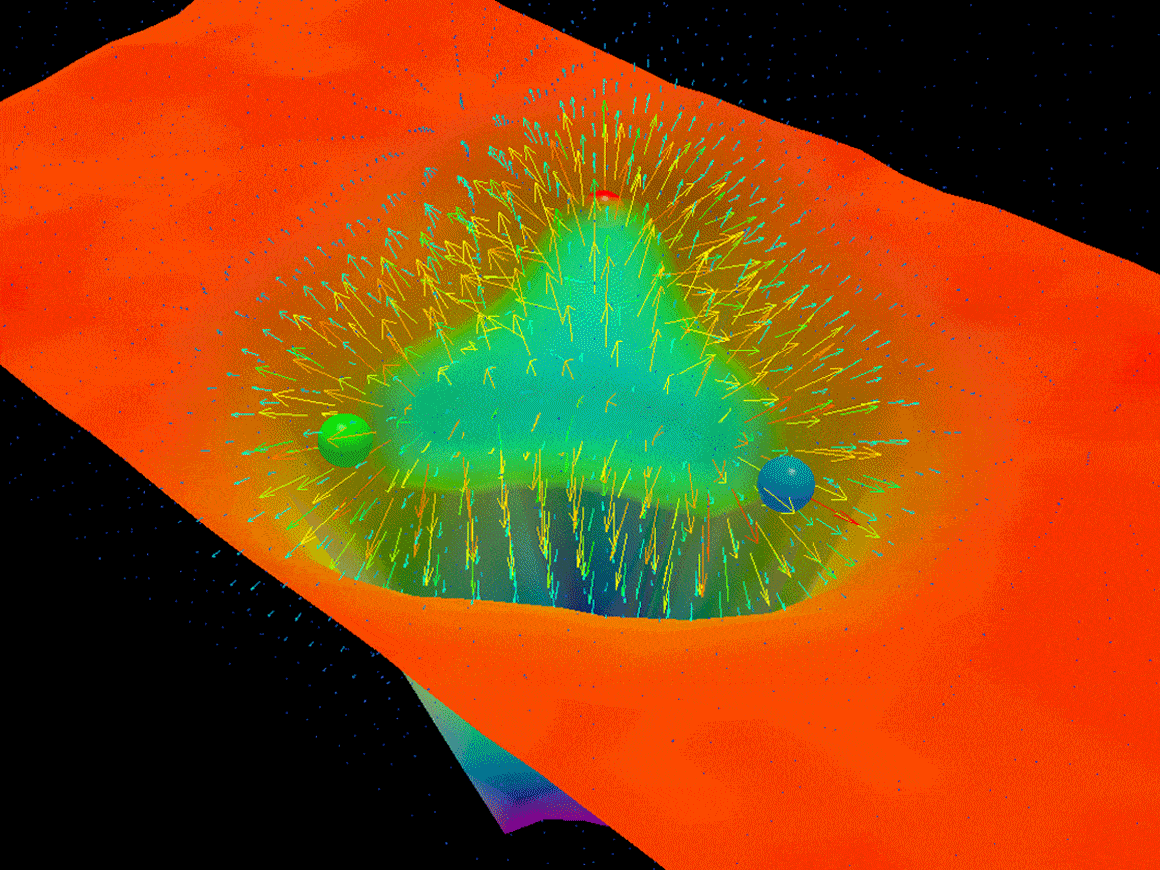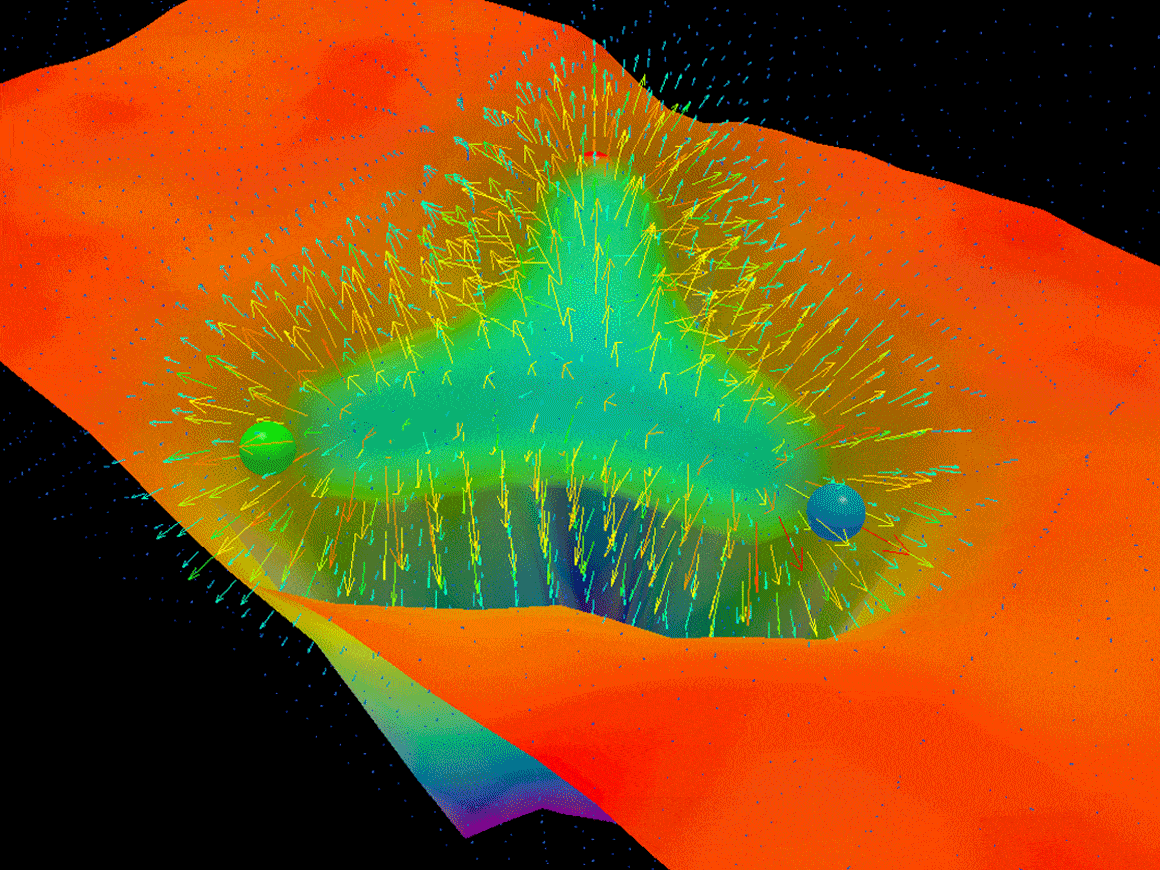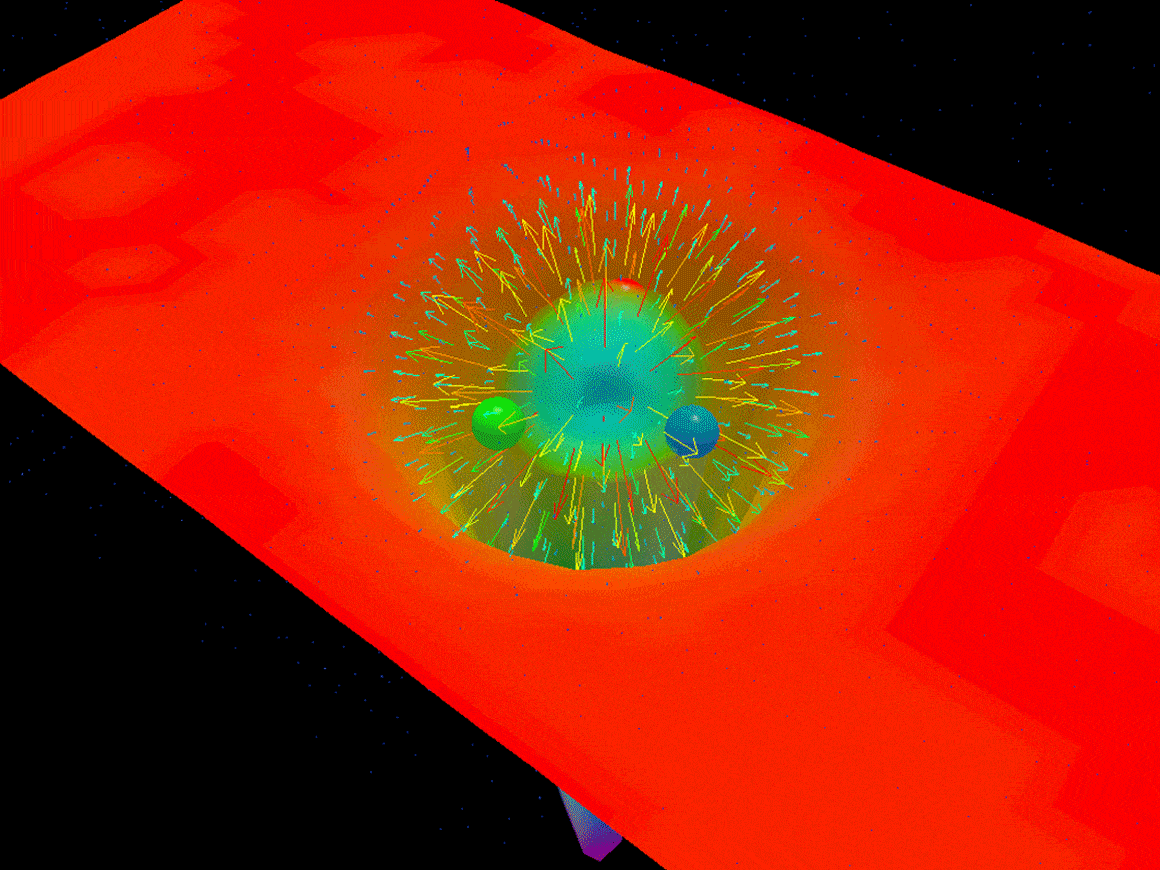
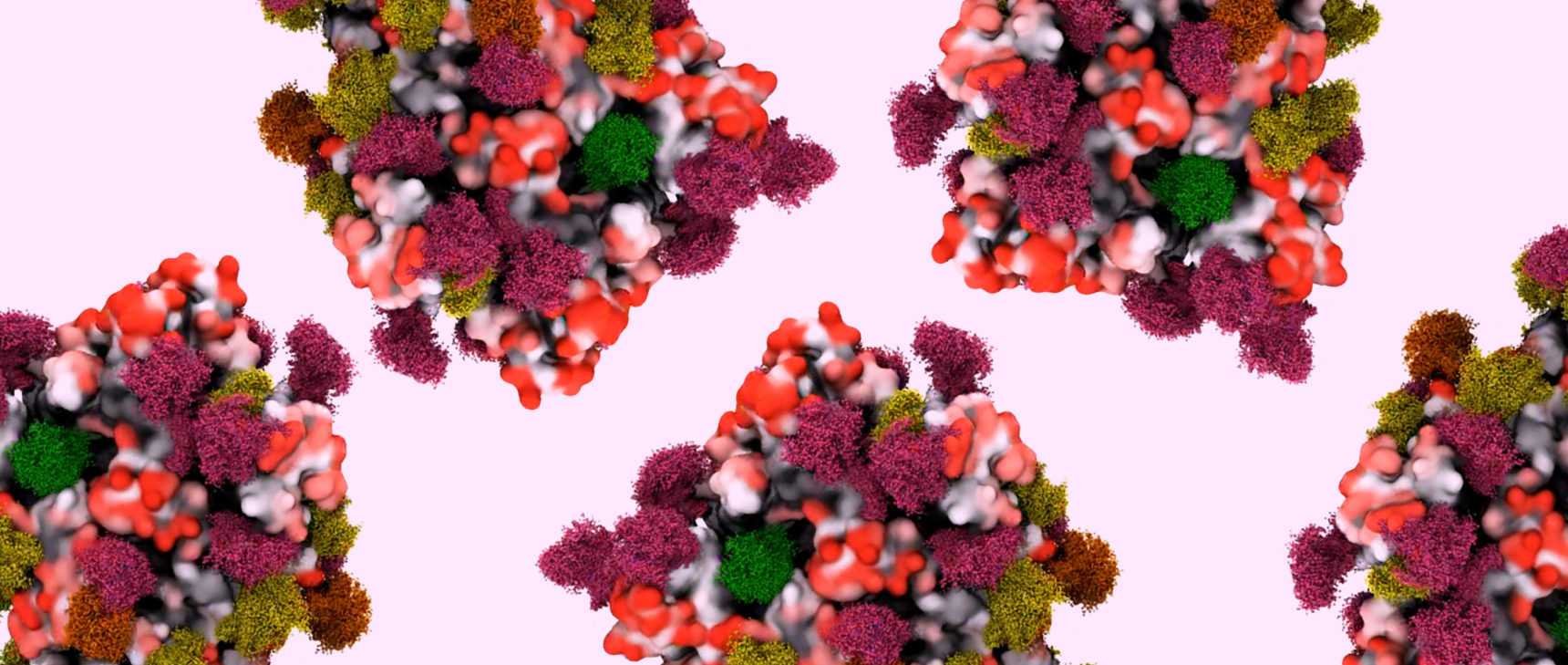
A proton consists of three quarks bound together by a field of gluons. These components were simulated using an approach called lattice QCD.
Derek Leinweber, CSSM, University of Adelaide
Introduction
Objects are made of atoms, and atoms are likewise the sum of their parts — electrons, protons and neutrons. Dive into one of those protons or neutrons, however, and things get weird. Three particles called quarks ricochet back and forth at nearly the speed of light, snapped back by interconnected strings of particles called gluons. Bizarrely, the proton’s mass must somehow arise from the energy of the stretchy gluon strings, since quarks weigh very little and gluons nothing at all.
Physicists uncovered this odd quark-gluon picture in the 1960s and matched it to an equation in the ’70s, creating the theory of quantum chromodynamics (QCD). The problem is that while the theory seems accurate, it is extraordinarily complicated mathematically. Faced with a task like calculating how three wispy quarks produce the hulking proton, QCD simply fails to produce a meaningful answer.
“It’s tantalizing and frustrating,” said Mark Lancaster, a particle physicist based at the University of Manchester in the United Kingdom. “We know absolutely that quarks and gluons interact with each other, but we can’t calculate” the result.
A million-dollar math prize awaits anyone who can solve the type of equation used in QCD to show how massive entities like protons form. Lacking such a solution, particle physicists have developed arduous workarounds that deliver approximate answers. Some infer quark activity experimentally at particle colliders, while others harness the world’s most powerful supercomputers. But these approximation techniques have recently come into conflict, leaving physicists unsure exactly what their theory predicts and thus less able to interpret signs of new, unpredicted particles or effects.
To understand what makes quarks and gluons such mathematical scofflaws, consider how much mathematical machinery goes into describing even well-behaved particles.
A humble electron, for instance, can briefly emit and then absorb a photon. During that photon’s short life, it can split into a pair of matter-antimatter particles, each of which can engage in further acrobatics, ad infinitum. As long as each individual event ends quickly, quantum mechanics allows the combined flurry of “virtual” activity to continue indefinitely.
In the 1940s, after considerable struggle, physicists developed mathematical rules that could accommodate this bizarre feature of nature. Studying an electron involved breaking down its virtual entourage into a series of possible events, each corresponding to a squiggly drawing known as a Feynman diagram and a matching equation. A perfect analysis of the electron would require an infinite string of diagrams — and a calculation with infinitely many steps — but fortunately for the physicists, the more byzantine sketches of rarer events ended up being relatively inconsequential. Truncating the series gives good-enough answers.
The discovery of quarks in the 1960s broke everything. By pelting protons with electrons, researchers uncovered the proton’s internal parts, bound by a novel force. Physicists raced to find a description that could handle these new building blocks, and they managed to wrap all the details of quarks and the “strong force” that binds them into a compact equation in 1973. But their theory of the strong force, quantum chromodynamics, didn’t behave in the usual way, and neither did the particles.
Feynman diagrams treat particles as if they interact by approaching each other from a distance, like billiard balls. But quarks don’t act like this. The Feynman diagram representing three quarks coming together from a distance and binding to one another to form a proton is a mere “cartoon,” according to Flip Tanedo, a particle physicist at the University of California, Riverside, because quarks are bound so strongly that they have no separate existence. The strength of their connection also means that the infinite series of terms corresponding to the Feynman diagrams grows in an unruly fashion, rather than fading away quickly enough to permit an easy approximation. Feynman diagrams are simply the wrong tool.
The strong force is weird for two main reasons. First, whereas the electromagnetic force involves just one variety of charge (electric charge), the strong force involves three: “color” charges nicknamed red, green and blue. Weirder still, the carrier of the strong force, dubbed the gluon, itself bears color charge. So while the (electrically neutral) photons that comprise electromagnetic fields don’t interact with each other, collections of colorful gluons draw together into strings. “That really drives the differences we see,” Lancaster said. The ability of gluons to trip over themselves, together with the three charges, makes the strong force strong — so strong that quarks can’t escape each other’s company.
Evidence piled up over the decades that gluons exist and act as predicted in certain circumstances. But for most calculations, the QCD equation has proved intractable. Physicists need to know what QCD predicts, however — not just to understand quarks and gluons, but to pin down properties of other particles as well, since they’re all affected by the dance of quantum activity that includes virtual quarks.
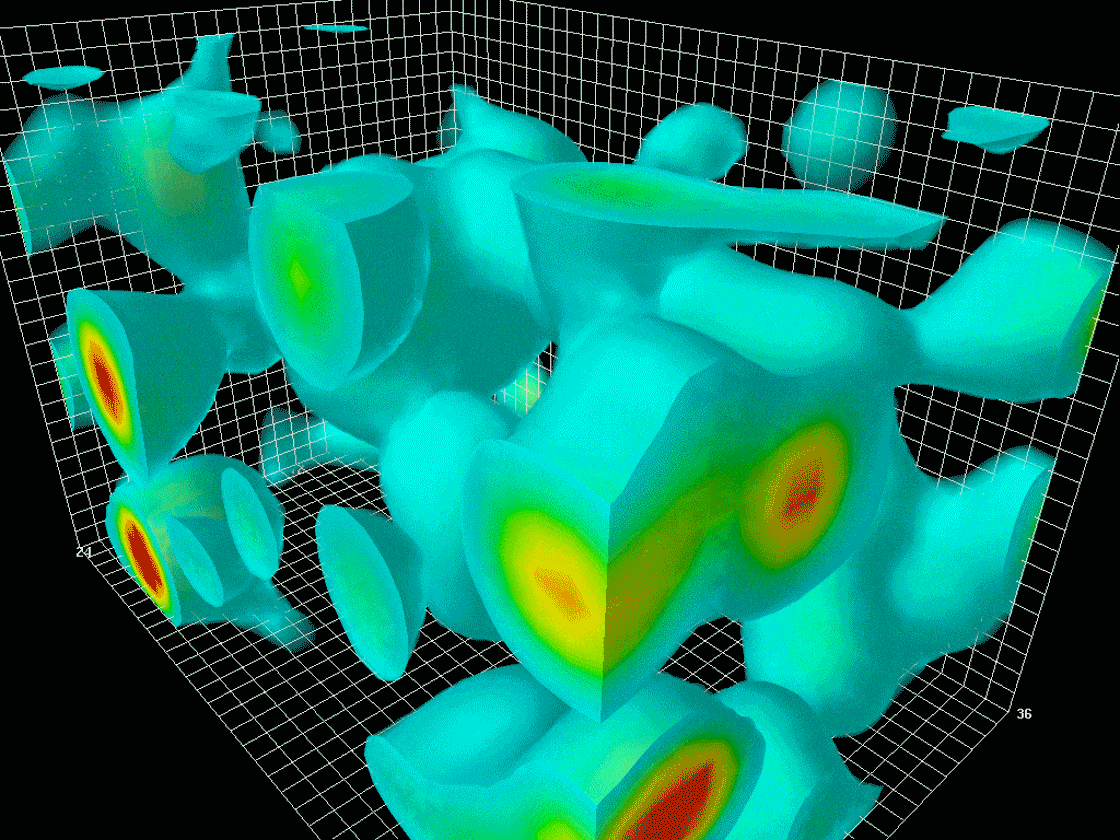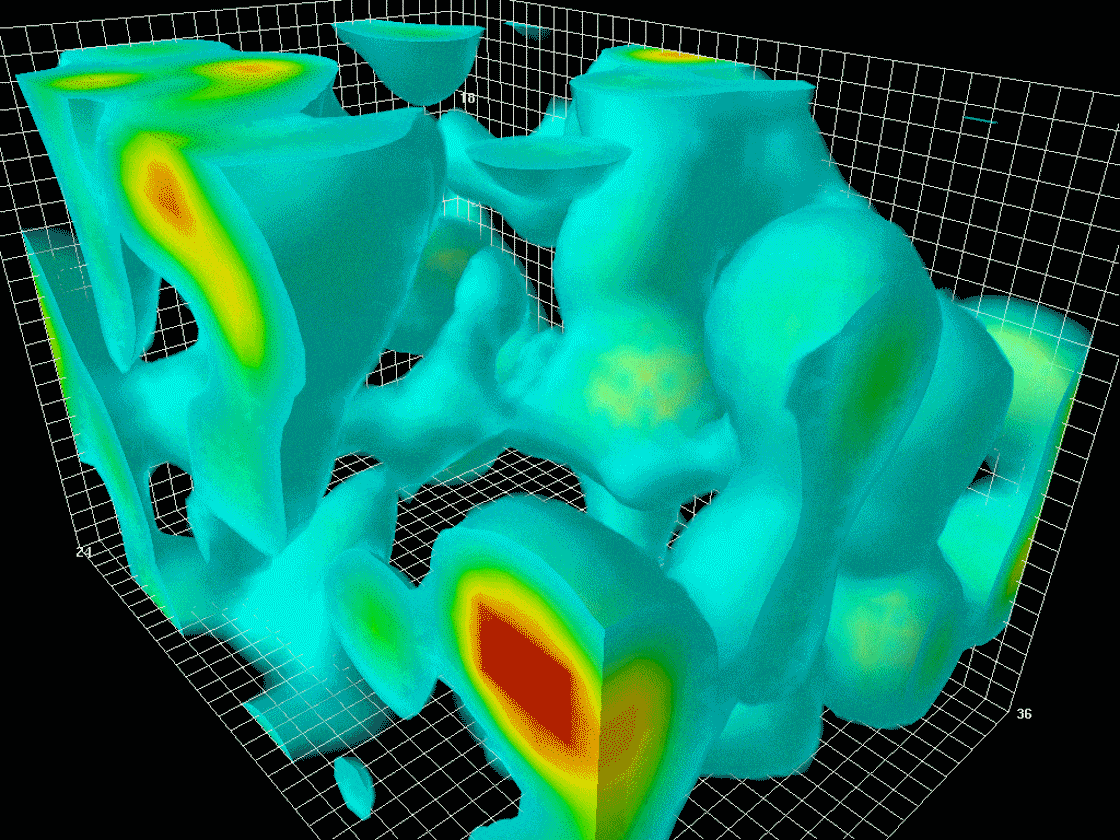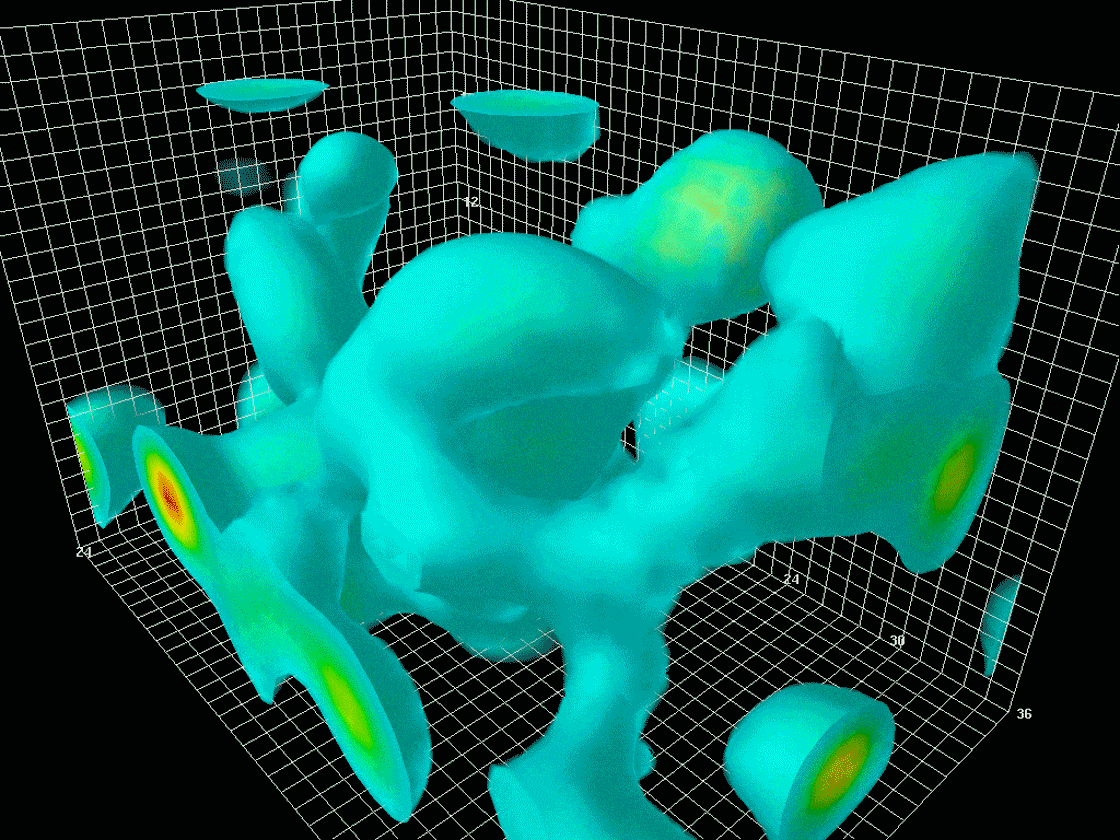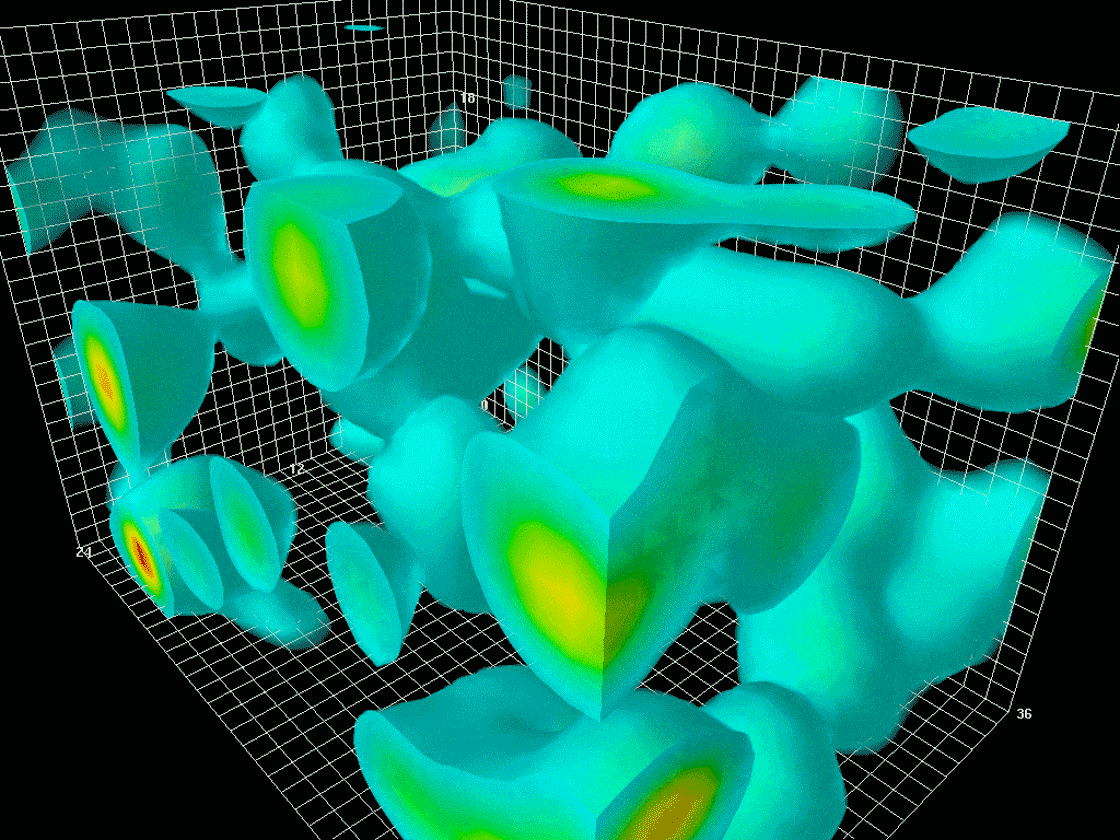
A lattice QCD simulation of an evolving field of gluons, with regions of highest energy density shown in red.
One approach has been to infer incalculable values by watching how quarks behave in experiments. “You take electrons and positrons and slam them together,” said Chris Polly, a particle physicist at the Fermi National Accelerator Laboratory, “and ask how often you make quark [products] in the final state.” From those measurements, he said, you can extrapolate how often quark bundles should pop up in the hubbub of virtual activity that surrounds all particles.
Other researchers have continued to try to wring information from the canonical QCD equation by calculating approximate solutions using supercomputers. “You just keep throwing more computing cycles at it and your answer will keep getting better,” said Aaron Meyer, a particle physicist at Brookhaven National Laboratory.
This computational approach, known as lattice QCD, turns computers into laboratories that model the behavior of digital quarks and gluons. The technique gets its name from the way it slices space-time into a grid of points. Quarks sit on the lattice points, and the QCD equation lets them interact. The denser the grid, the more accurate the simulation. The Fermilab physicist Andreas Kronfeld remembers how, three decades ago, these simulations had just a handful of lattice points on a side. But computing power has increased, and lattice QCD can now successfully predict the proton’s mass to within a few percent of the experimentally determined value.
Kronfeld is a spokesperson for USQCD, a federation of lattice QCD groups in the United States that have banded together to negotiate for bulk supercomputer time. He serves as the principal investigator for the federation’s efforts on the Summit supercomputer, currently the world’s fastest, located at Oak Ridge National Laboratory. USQCD runs one of Summit’s largest programs, occupying nearly 4% of the machine’s annual computing capacity.
Theorists thought these digital laboratories were still a year or two away from becoming competitive with the collider experiments in approximating the effects quarks have on other particles. But in February a European collaboration shocked the community with a preprint claiming to nail a magnetic property of a particle called the muon to within 1% of its true value, using novel noise reduction techniques. “You might think of it as throwing down the gauntlet,” said Aida El-Khadra, a high-energy theorist at the University of Illinois, Urbana-Champaign.
The team’s prediction for virtual quark activity around the muon clashed with the inferences from electron-positron collisions, however. Meyer, who recently co-authored a survey of the conflicting results, says that many technical details in lattice QCD remain poorly understood, such as how to hop from the gritty lattice back to smooth space. Efforts to determine what QCD predicts for the muon, which many researchers consider a bellwether for undiscovered particles, are ongoing.
Meanwhile, mathematically minded researchers haven’t entirely despaired of finding a pen-and-paper strategy for tackling the strong force — and reaping the million-dollar reward offered by the Clay Mathematics Institute for a rigorous prediction of the mass of the lightest possible collection of quarks or gluons.
One such Hail Mary pass in the theoretical world is a tool called the holographic principle. The general strategy is to translate the problem into an abstract mathematical space where some hologram of quarks can be separated from each other, allowing an analysis in terms of Feynman diagrams.
Simple attempts look promising, according to Tanedo, but none come close to the hard-won accuracy of lattice QCD. For now, theorists will continue to refine their imperfect tools and dream of new mathematical machinery capable of taming the fundamental but inseparable quarks.
“That would be the holy grail,” Tanedo says. QCD is “just begging for us to figure out how that actually works.”
This article was reprinted on Wired.com and in Spanish at Investigacionyciencia.es.