Common Sense Comes Closer to Computers
Add a match to a pile of wood. What do you get? For a human, it’s easy. But machines have long lacked the common-sense reasoning abilities needed to figure it out.
Guillem Casasús Xercavins for Quanta Magazine
Introduction
One evening last October, the artificial intelligence researcher Gary Marcus was amusing himself on his iPhone by making a state-of-the-art neural network look stupid. Marcus’ target, a deep learning network called GPT-2, had recently become famous for its uncanny ability to generate plausible-sounding English prose with just a sentence or two of prompting. When journalists at The Guardian fed it text from a report on Brexit, GPT-2 wrote entire newspaper-style paragraphs, complete with convincing political and geographic references.
Marcus, a prominent critic of AI hype, gave the neural network a pop quiz. He typed the following into GPT-2:
What happens when you stack kindling and logs in a fireplace and then drop some matches is that you typically start a …
Surely a system smart enough to contribute to The New Yorker would have no trouble completing the sentence with the obvious word, “fire.” GPT-2 responded with “ick.” In another attempt, it suggested that dropping matches on logs in a fireplace would start an “irc channel full of people.”
Marcus wasn’t surprised. Common-sense reasoning — the ability to make mundane inferences using basic knowledge about the world, like the fact that “matches” plus “logs” usually equals “fire” — has resisted AI researchers’ efforts for decades. Marcus posted the exchanges to his Twitter account with his own added commentary: “LMAO,” internet slang for a derisive chortle. Neural networks might be impressive linguistic mimics, but they clearly lacked basic common sense.
Minutes later, Yejin Choi saw Marcus’ snarky tweet. The timing was awkward. Within the hour Choi was scheduled to give a talk at a prominent AI conference on her latest research project: a system, nicknamed COMET, that was designed to use an earlier version of GPT-2 to perform common-sense reasoning.
Quickly, Choi — a computer scientist at the University of Washington and the Allen Institute for Artificial Intelligence — fed COMET the same prompt Marcus had used (with its wording slightly modified to match COMET’s input format):
Gary stacks kindling and logs and drops some matches
COMET generated 10 inferences about why Gary might be dropping the matches. Not all of the responses made sense, but the first two did: He “wanted to start a fire” or “to make a fire.” Choi tweeted the results in reply to Marcus and strode up to the podium to include them in her presentation. “It seemed only appropriate,” she said.

Two Paths to Common Sense
Common sense has been called the “dark matter of AI” — both essential and frustratingly elusive. That’s because common sense consists of implicit information — the broad (and broadly shared) set of unwritten assumptions and rules of thumb that humans automatically use to make sense of the world. For example, consider the following scenario:
A man went to a restaurant. He ordered a steak. He left a big tip.
If you were asked what he ate, the answer — steak — comes effortlessly. But nowhere in that little scene is it ever stated that the man actually ate anything. When Ray Mooney, director of the Artificial Intelligence Laboratory at the University of Texas, Austin, pointed this out after giving me the same pop quiz, I didn’t believe him at first. “People don’t even realize that they’re doing this,” he said. Common sense lets us read between the lines; we don’t need to be explicitly told that food is typically eaten in restaurants after people order and before they leave a tip.
Computers do. It’s no wonder that common-sense reasoning emerged as a primary concern of AI research in 1958 (in a paper titled “Programs With Common Sense”), not long after the field of AI was born. “In general, you can’t do natural language understanding or vision or planning without it,” said Ernest Davis, a computer scientist at New York University who has studied common sense in AI since the 1980s.
Still, progress has been infamously slow. At first, researchers tried to translate common sense into the language of computers: logic. They surmised that if all the unwritten rules of human common sense could be written down, computers should be able to use them to reason with in the same way that they do arithmetic. This symbolic approach, which came to be known as “good old-fashioned artificial intelligence” (or GOFAI), enabled some early successes, but its handcrafted approach didn’t scale. “The amount of knowledge which can be conveniently represented in the formalisms of logic is kind of limited in principle,” said Michael Witbrock, an AI researcher at the University of Auckland in New Zealand. “It turned out to be a truly overwhelming task.”
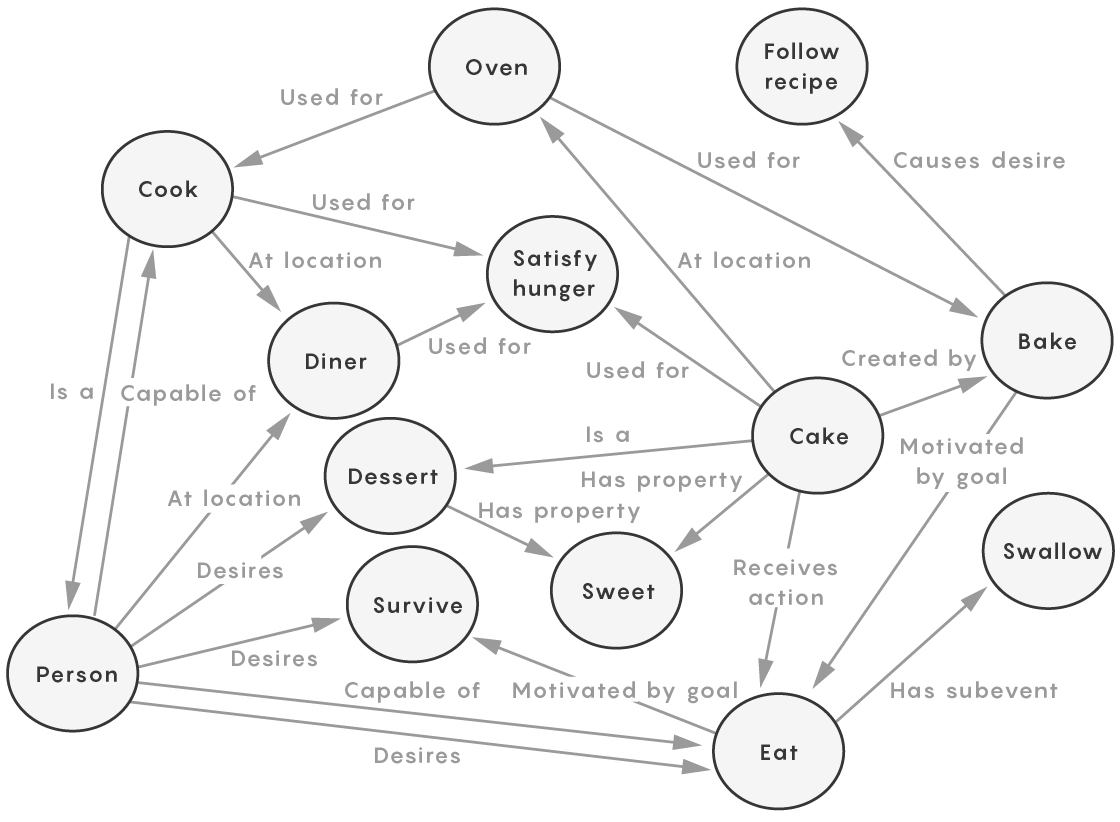
Even modest attempts to map all possible logical relationships quickly run into trouble. Some of the relationships above always hold (for example, swallowing is always a part of eating). Some hold only occasionally (a person eats at a diner). Some are inconsistent (a person can not eat a cake while it is also in the oven). And nodes such as “cook” can mean both a person who cooks and the activity of cooking.
doi: 10.1109/MIS.2009.72
Deep learning with neural networks seemed to offer an alternative. These AI systems, designed to mimic the interconnected layers of neurons in biological brains, learn patterns without requiring programmers to specify them in advance. Over the past decade, increasingly sophisticated neural networks, trained with copious amounts of data, have revolutionized computer vision and natural language processing. But for all their flexibility and apparent intellectual power — neural networks can now steer cars in highway traffic and beat world-class players at chess and Go — these systems remain notorious for their own silly (and occasionally fatal) lapses in ordinary common sense. “Acquiring it, representing it, reasoning with it — it’s all hard,” Davis said.
Now, Choi and her collaborators have united these approaches. COMET (short for “commonsense transformers”) extends GOFAI-style symbolic reasoning with the latest advances in neural language modeling — a kind of deep learning that aims to imbue computers with a statistical “understanding” of written language. COMET works by reimagining common-sense reasoning as a process of generating plausible (if imperfect) responses to novel input, rather than making airtight deductions by consulting a vast encyclopedia-like database.
“It tries to blend two very fundamentally different approaches to AI,” said Mooney, who is already using COMET in his own research. “It’s an interesting new direction that says, ‘Hey, there’s a middle road there.’” Leora Morgenstern, an expert in common-sense reasoning and AI at the Palo Alto Research Center who has spent decades researching symbolic approaches to the problem, thinks that the ideas behind COMET can help move the field forward. “One of the reasons I’m so excited about what Yejin is doing is I think it will inject new life into the common-sense reasoning community,” she said. “Deep learning is really, really powerful — let’s figure out how to harness it for common sense.”

Endless Unwritten Rules
Common sense is easier to detect than to define. According to Witbrock, the phrase “common sense” can mean both a kind of knowledge and an attitude toward that knowledge. “I would say [it’s] broadly reusable background knowledge that’s not specific to a particular subject area,” he said. “It’s knowledge that you ought to have.” Like, for example, the fact that people eat food in restaurants, rather than just ordering and paying for it; or that dropping matches on a pile of stacked logs implies that one is trying to light a fire.
The implicit nature of most common-sense knowledge makes it difficult and tedious to represent explicitly. “What you learn when you’re two or four years old, you don’t really ever put down in a book,” said Morgenstern. Nevertheless, early AI researchers believed that bridging this gap was possible. “It was like, ‘Let’s write down all the facts about the world. Surely there’s only a couple million of them,’” said Ellie Pavlick, a computer scientist at Brown University. Constructing such a resource, known as a knowledge base, has traditionally been the first step in any approach to automating common-sense reasoning.
Building up a sufficient number of obvious facts is harder than it sounds. A common-sense reasoning project called Cyc began in 1984 with the modest-sounding goal of encoding the implicit common-sense knowledge necessary to represent 400 encyclopedia articles. It never stopped. More than three decades later, Cyc’s knowledge base — encoded in a dense, custom-designed logical notation — contains “millions of collections and concepts, and more than 25 million assertions.” Yet a 2015 review article by Davis and Marcus stated that “Cyc has had comparatively little impact on AI research.” Subsequent attempts to write entries for a knowledge base — or to create one by mining documents using machine learning — have failed to crack the common-sense reasoning problem.
Why? For one thing, “there’s always exceptions to every case,” Pavlick explained. “If I hear some statement like ‘it’s raining,’ I could infer that if I go outside I’ll get wet, but not if [I’m] underneath something.” Other exceptions are harder to anticipate. A knowledge base like Cyc may contain dozens of statements about what typically happens when a person orders food in a restaurant. But what about the potentially endless list of infrequent or unusual things that could happen in that scenario, like leaving without paying the check, or starting a food fight? “Coverage is never-ending,” said Choi. “Therefore, purely symbolic knowledge-based approaches are entirely doomed.”
Even if it were possible to build a knowledge base 100 or 1,000 times as comprehensive as any previous attempt, the system would still suffer from another intellectual shortcoming: the so-called brittleness problem. That’s because common sense, like natural language, remains fundamentally fuzzy. When a server asks a diner, “Are you still working on that?” we understand them to mean “Are you still eating what’s on your plate?” But if the server asks the same question to a line cook preparing an overdue order, it means something else entirely. So is a restaurant a place where people “work” on things? Are “eating” and “working” distinct concepts?
It all depends. That’s the brittleness problem: Sharply defined relations within a knowledge base may enable powerful, reliable reasoning abilities, as long as those conceptual edges are respected. But these symbolic systems, no matter how varied and rich, inevitably fail to capture the natural ambiguities and associative overlaps that often occur in human common-sense reasoning. “To the extent that we [use] symbols,” Pavlick said, “we’re quite fluid with them.”

Going Neural
Choi didn’t start working on common sense because she wanted to tilt at windmills. When she joined the Allen Institute in 2018, she “had a hunch” that neural networks could enable new progress where knowledge bases had stalled on their own. She just didn’t know exactly how. She didn’t want to write off previous symbolic approaches completely, either. “All the past research was based on a lack of data,” she said, or a lack of computing resources. “So I figured I’d just withhold my judgment until I properly tried different routes.”
With an open mind, Choi and her colleagues began to assemble their own knowledge base called Atomic (short for “atlas of machine commonsense”). “Basically, I wanted to write a textbook for neural networks to learn faster about the world,” Choi said. “Then things happened simultaneously — as we had this knowledge [base] built, GPT-2 came out.”
That neural network, released in February 2019, was just one in a wave of “pre-trained language models” that began to revolutionize how computers process natural language. These systems don’t contain neatly organized linguistic symbols or rules. Instead, they statistically smear their representations of language across millions or billions of parameters within a neural network. This property makes such systems difficult to interpret, but it also makes them robust: They can generate predictions based on noisy or ambiguous input without breaking. When fine-tuned to perform a specific task — like answering written questions or paraphrasing text — language models even appear to understand at least some of what they’re reading.
Choi now saw a way to put her hunch about neural networks and common sense into action.
What would happen if a language model were given additional training using a common-sense knowledge base, like Atomic? Could the neural network learn to fill in Atomic’s gaps with plausible commonsense inferences all on its own, just as GPT-2 learned how to automatically generate plausible news articles? “It’s almost weird that nobody tried this before,” Choi said. “It’s almost as if nobody bothered because they were so sure this would never work.”
When Choi (and her collaborators Antoine Bosselut, Hannah Rashkin, Maarten Sap, Chaitanya Malaviya and Asli Celikyilmaz) fine-tuned a neural language model with the common-sense knowledge encoded in Atomic, they created COMET. Its fusion of symbolic reasoning with a neural network tries to solve the coverage and brittleness problems at the same time. Anyone can type a prompt into COMET in everyday language. If the event is already represented in the system’s common-sense knowledge base (like the fact that ordering food in a restaurant usually involves eating it), COMET can simply reason with that preexisting information. For everything else, the neural language model makes its best guess.
Those guesses are surprisingly good. On average, 77.5% of the novel responses generated by COMET — that is, inferences that come from the neural network, rather than from the preexisting knowledge base — were deemed “plausible” by teams of human evaluators. That’s less than 10 percentage points shy of human-level performance. (Evaluators found 86% of knowledge-base entries written by humans to be plausible.) When COMET was given the prompt “PersonX gives PersonY some pills,” it guessed that PersonX wanted to help; when it was told that “PersonX murders PersonY’s wife,” COMET suggested that PersonX wanted to hide the body.
These examples showed how COMET could handle input beyond the limits of its built-in common-sense “coverage.” But what about the brittleness problem? While interviewing Choi late last year at her lab in Seattle, I gave COMET a prompt phrased in my 5-year-old daughter’s patois: “Daddy goed to work.”
Choi frowned. “That may be tricky,” she said. But COMET took it in stride, suggesting that “Daddy” wanted to “make money,” “do their job” and “get a paycheck”; that he is seen as “hardworking,” “motivated” and “dutiful”; and that as a result, others feel “proud,” “grateful” and — in an amusingly plausible response, given that the request was written in kindergartner-speak — “annoyed.” (My daughter has certainly expressed that sentiment when I leave for work instead of playing with her.) “This wouldn’t work with Cyc, for sure,” Choi remarked. “Unless someone hand-codes that ‘goed’ means ‘went’ — which we never did.”

Ladders and Rockets
There’s a quip Gary Marcus likes to use to put progress in AI into context: “Just because you can build a better ladder doesn’t mean you can build a ladder to the moon.” To him and others, COMET’s approach suffers from a fundamental limitation of deep learning: “statistics ≠ understanding.” “You can see that [COMET] does a decent job of guessing some of the parameters of what a sentence might entail, but it doesn’t do so in a consistent way,” Marcus wrote via email. Just as no ladder, no matter how tall, can ever hope to reach the moon, no neural network — no matter how deft at mimicking language patterns — ever really “knows” that dropping lit matches on logs will typically start a fire.
Choi, surprisingly, agrees. She acknowledged that COMET “relies on surface patterns” in its training data, rather than actual understanding of concepts, to generate its responses. “But the fact that it’s really good at surface patterns is a good thing,” she said. “It’s just that we’ve got to supply it with more informative surface patterns.”
What might those more informative patterns look like? Some researchers argue that in order to build real common sense into computers, we will need to make use of phenomena outside language itself, like visual perceptions or embodied sensations. These more direct first-person representations may be the foundation of common sense, with language acting as a secondary layer.
“If I lived in a world where there were no other people [to talk to], I could still have common sense — I’d still understand how the world works and have expectations over what I should see and shouldn’t see,” said Pavlick, who is currently studying how to teach AI systems common sense by interacting with them in virtual reality. To her, COMET represents “really exciting progress, but what’s missing is the actual reference aspect. The word ‘apple’ is not an apple. That meaning has to exist in some form that’s not the language itself.”
Nazneen Rajani, a senior research scientist at Salesforce, is pursuing a similar goal, but she believes the full potential of neural language models is far from tapped. She’s investigating whether they can learn to reason about common-sense scenarios involving basic physics, like the fact that tipping over a jar with a ball inside will typically cause the ball to drop out. “The real world is really complicated,” Rajani said. “But natural language is like a low-dimensional proxy for how the real world works.” Sure, neural networks can be taught to predict the next word from a text prompt, but that shouldn’t be their limit. “They can learn more complex stuff.”
Choi and her colleagues are also working on ways to augment COMET with labeled visual scenes instead of just text. “We took all these images from movies or TV shows where some interesting things are happening,” Choi said. “The annotations look great; the model predictions look exciting.”
I asked Choi if COMET’s approach — combining incrementally better neural networks with improved common-sense knowledge bases — was still, essentially, building a ladder to the moon. She conceded that her dream would be to have a neural network that could learn from knowledge bases without human supervision, the same way language models like GPT-2 already learn by ingesting reams of raw text.
But just as Winston Churchill quipped that “democracy is the worst form of government except for all those other forms that have been tried,” Choi considers COMET’s flawed but promising approach to be “a fair deal.” Even if these neural networks can’t reach the stars, she thinks they’re the only way to get off the ground. “Without that, we are not going anywhere,” she said. “With [knowledge bases] alone, we cannot do anything. It’s COMET that can actually fly in the air.”
Update May 1, 2020: This article was updated to include Choi’s affiliation with the University of Washington.
This article was reprinted on TheAtlantic.com.



