Pentagon Tiling Proof Solves Century-Old Math Problem
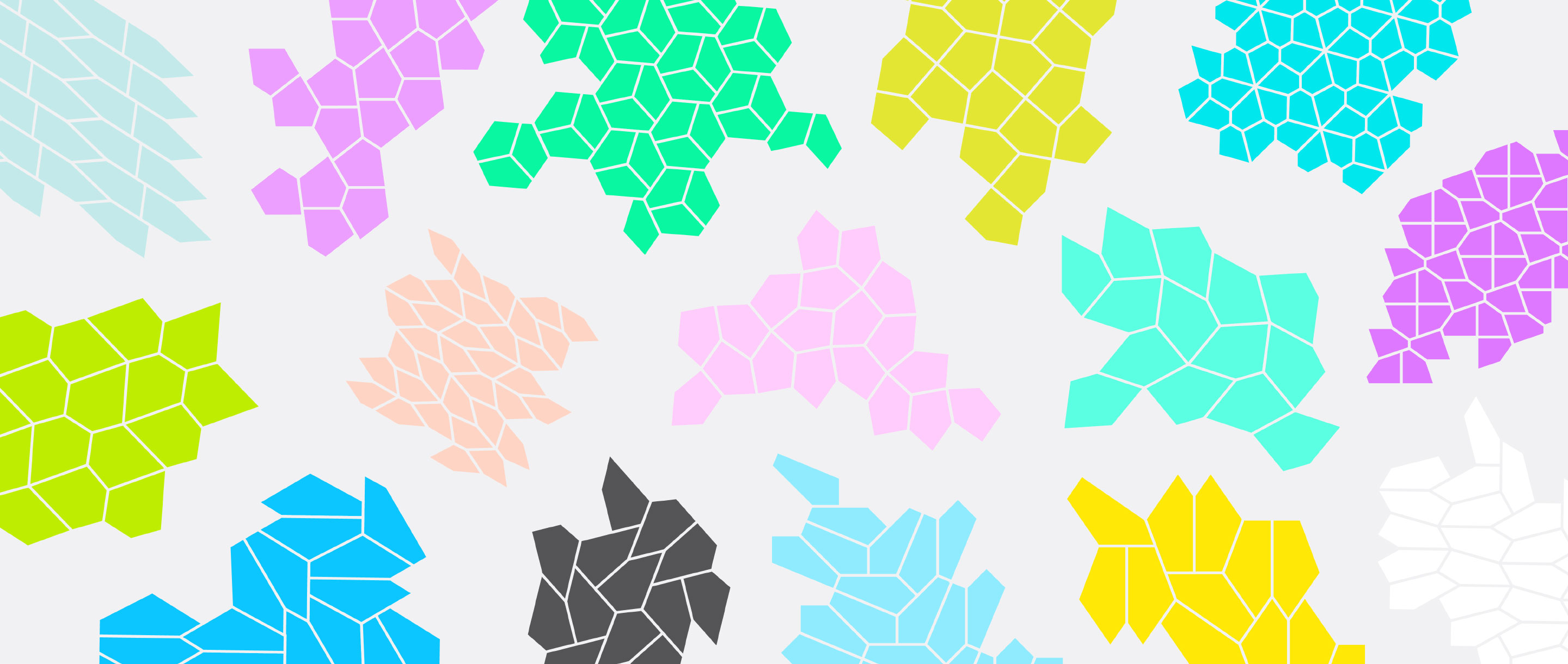
Representatives of the 15 families of convex pentagons that tile the plane.
Olena Shmahalo/Quanta Magazine
Introduction
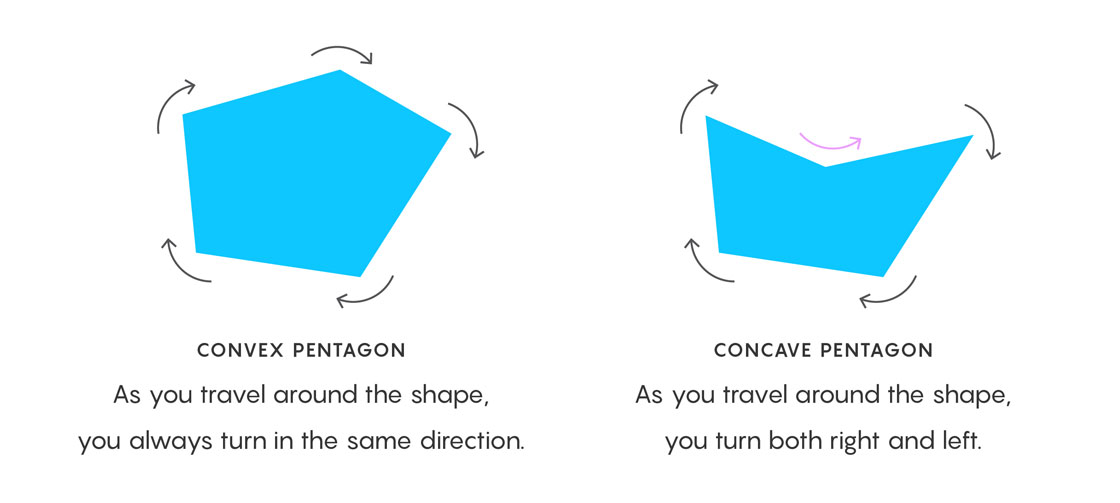
One of the oldest problems in geometry asks which shapes tile the plane, locking together with copies of themselves to cover a flat area in an endless pattern called a tessellation. M.C. Escher’s drawings of tessellating lizards and other creatures illustrate that an unlimited variety of shapes can do this. The inventorying reduces to a finite, though still formidable, task when mathematicians consider only convex polygons: simple, flat-edged shapes like triangles and rectangles whose angles all bend in the same direction. Now, a new proof by Michaël Rao, a 37-year-old mathematician at CNRS (France’s national center for scientific research) and the École Normale Supérieure de Lyon, finally completes the classification of convex polygons that tile the plane by conquering the last holdouts: pentagons, which have resisted sorting for 99 years.
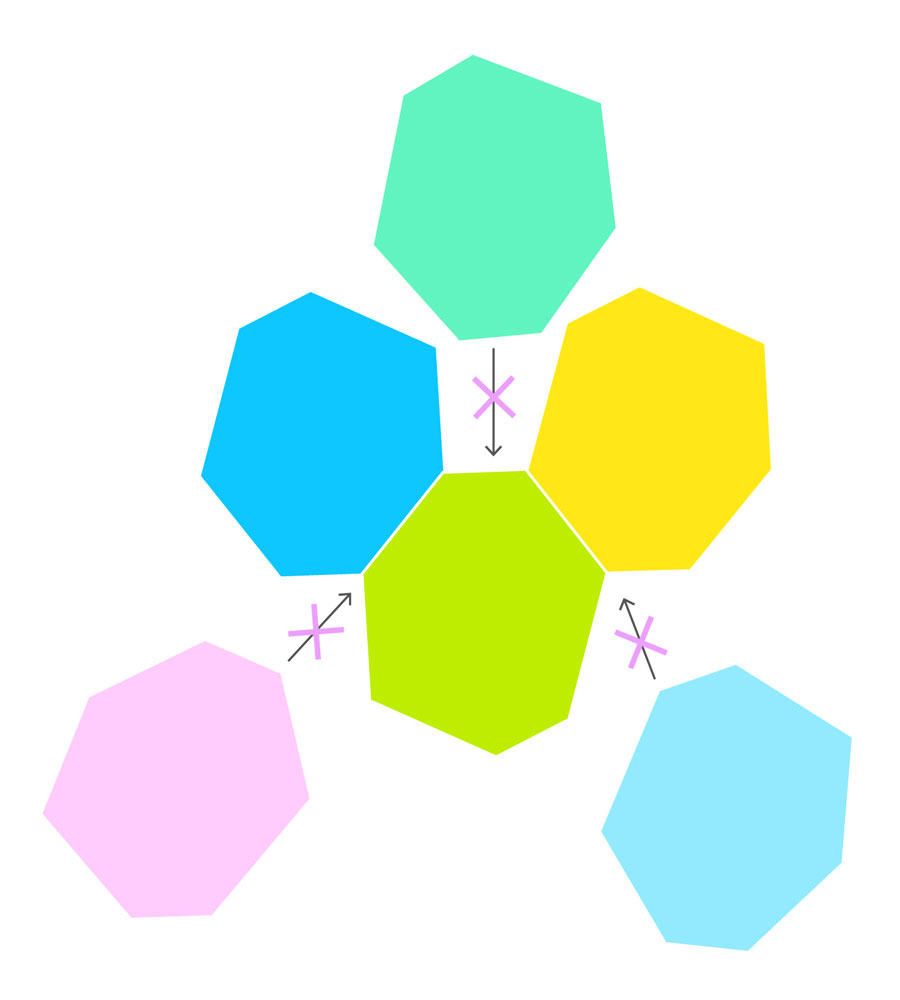
Try placing regular pentagons — those with equal angles and sides — edge to edge and gaps soon form; they do not tile. The ancient Greeks proved that the only regular polygons that tile are triangles, quadrilaterals and hexagons (as now seen on many a bathroom floor). But squash and stretch a pentagon into an irregular shape and tilings become possible. In his 1918 doctoral thesis, the German mathematician Karl Reinhardt identified five types of irregular convex pentagons that tile the plane: They were families defined by common rules, such as “side a equals side b,” “c equals d,” and “angles A and C both equal 90 degrees.”
Reinhardt didn’t know whether his five families completed the list, and progress stalled for 50 years. Then, in 1968, Richard Kershner of Johns Hopkins University discovered three more types of tessellating convex pentagons and claimed to have proved that no others existed. But Kershner’s paper left out the proof that his list was exhaustive “for the excellent reason,” reads an introductory note, “that a complete proof would require a rather large book.”

Marjorie Rice’s Secret Pentagons

Michaël Rao of CNRS (France’s national center for scientific research) and the École Normale Supérieure de Lyon.
Etienne Moutot
News of Kershner’s pentagon claim spread to the masses in 1975 when it appeared in Martin Gardner’s popular math column in Scientific American. But soon after, lay readers like Marjorie Rice, a San Diego housewife with a high school math education, discovered new tessellating pentagon families beyond those known to Kershner. (Rice found four and a computer programmer named Richard James found one.) The list of families grew to 13 and, in 1985, to 14. Then, in 2015, Casey Mann, an associate professor of mathematics at the University of Washington, Bothell, and collaborators used a computer search to discover a 15th type of tessellating convex pentagon.
When Rao heard about Mann and his team’s discovery, he set out to do an exhaustive search that would complete the classification of tessellating convex pentagons once and for all.
In his new computer-assisted proof, Rao identified 371 possible scenarios for how corners of pentagons might come together in a tiling, and then he checked them all. In the end, his algorithm determined that only the 15 known pentagon families can do it. His proof closes the field of convex polygons that tile the plane at 15 pentagons, three types of hexagons — all identified by Reinhardt in his 1918 thesis — and all quadrilaterals and triangles. (No tilings by convex polygons with seven or more sides exist.)
Mann said he and his collaborators had been working on taking a partial step toward an exhaustive proof when they heard the news from France. “Rao beat us to the punch,” he said, adding wryly, “Which is great, because it saves us a lot of work.”
Thomas Hales, a professor of mathematics at the University of Pittsburgh and a leader in using computer programming to solve problems in geometry, has independently reproduced the most important half of Rao’s proof, indicating that there isn’t a bug. Rao still has to submit the proof for peer-reviewed publication, but Hales already feels confident that it holds up.
As one journey — the classification of all convex polygon tessellations — ends, another is just beginning. Rao, like many tiling specialists, seeks the elusive “einstein,” a hypothetical shape that can only tile the plane nonperiodically, in a pattern of tile orientations that never repeats. Its name has nothing to do with the famous physicist but rather is German for “one stone.” “For everybody who works on tiling, this is a kind of holy grail,” Rao said. He sees his pentagon proof as an early milestone on this much larger quest.
Good Sets
In his proof, Rao first showed that there are only a finite number of scenarios for how the corners of convex pentagons can fit together that need to be checked for tessellations. He used simple geometric conservation laws to impose restrictions on how a pentagon’s corners — labeled 1 to 5 — can possibly meet at the vertices in a tiling. These conditions include the fact that the sum of angles 1 to 5 must equal 540 degrees — the total for any pentagon — and that all five have to participate in a tiling equally, since they’re all part of every pentagonal tile. Moreover, the sums of the angles at a given vertex must always equal either 360 degrees, if the corners of the adjacent pentagons all meet there, or 180 degrees, if some corners meet along another pentagon’s edge.
By imposing such rules, Rao found that other than for 371 scenarios, “either the angle equations or the percentages [dictating how often different angles appear] self-contradict,” said Greg Kuperberg, a professor of mathematics at the University of California, Davis. A finite number of “good sets,” as Rao dubbed the possible sets of angle conditions, wasn’t guaranteed, Kuperberg said, “but his computer run delivered good news.”
In the second of the two main steps in his proof, Rao went through the good sets one by one and checked whether any tilings satisfying these angle conditions existed. When it came to the coding, this was “the more complicated part,” Rao said.
“For each of the 371 scenarios,” Kuperberg explained, “his algorithm tries to piece together a tiling by laying down one tile at a time, using only the allowed vertex configurations.” In searching through these 371 trees of possibilities, the algorithm either determined that every path in a tree leads to a pentagon in one of the 15 known families, or that “all paths on the tree lead to grief after a finite number of steps,” explained Rich Schwartz, a mathematician at Brown University who works on related problems.
Rao said he felt disappointed not to have discovered any additional families, but tiling experts say that proving a complete list of 15 is more significant than simply finding a new working example.
The exhaustive proof also helps direct the search for the hypothetical einstein — that coveted puzzle piece that locks together with itself in an ever-changing sequence of tile orientations.
“One conclusion from Rao’s breakthrough result is that there is no single convex polygon that tiles the plane nonperiodically,” Kuperberg said. Since all 15 of the tessellating convex pentagons (and all other convex polygons) tile the plane periodically, meaning in a sequence of tile orientations that regularly repeats, the einstein, if it exists, must be concave, with jagged corners that bend both inward and outward like the corners of a star.
Seeking Einstein
Experts say there’s good reason to think that the einstein exists, though its shape is probably very complex. That such an elusive shape would be needed to tessellate the plane nonperiodically only adds to its allure.

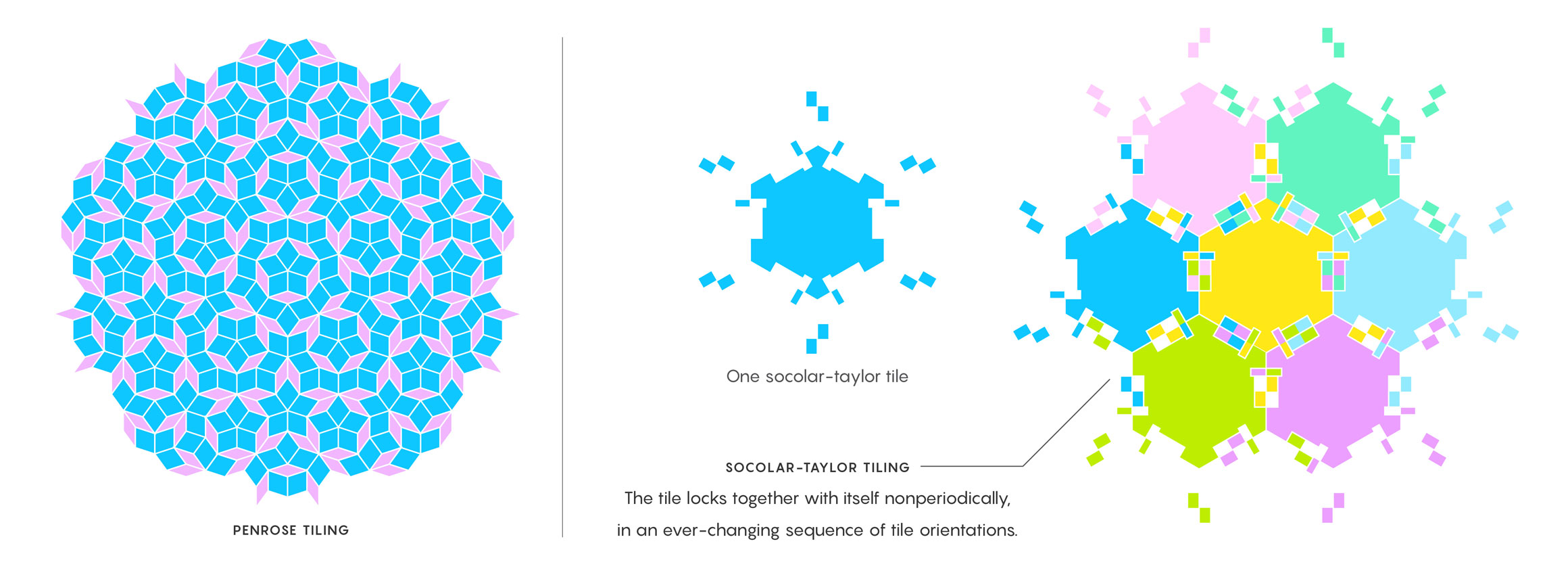
Lucy Reading-Ikkanda/Quanta Magazine, adapted from Inductiveload (left) and Joshua Socolar and Joan Taylor
Nonperiodic tilings exist when you have tiles of at least two different shapes to play with —an example is the famous Penrose tiling — or when using a bizarre tile consisting of parts that are not connected, called the Socolar-Taylor tile. But whether a single connected tile exists that can do the job, and what its properties might be, remains unknown. Mann said the einstein’s existence is “considered likely because it’s connected to another very central problem in tiling theory” called the decision problem. “The question is, if someone hands you a tile, can you come up with a computer algorithm that will take as input that tile and say, ‘Yes, this tiles the plane,’ or, ‘No, it doesn’t’?”
“Most people think there’s too much complexity for such an algorithm to exist,” Mann said. Researchers have already proved that no algorithm exists that can decide if an arbitrary collection of different shapes tiles the plane. Many experts suspect, though it isn’t proven, that the single-tile decision problem is “undecidable” as well. In a backward kind of way, this would imply the existence of the einstein tile. Since “it’s pretty easy to check if something is periodic,” Mann said, the decision problem should be decidable if single shapes only ever tile the plane periodically. The existence of the einstein tile and the hardness of the single-tile decision problem go hand in hand.
Rao plans to put his algorithms on the einstein’s trail, though he says concave shapes represent a much bigger combinatorial problem than convex ones. Other experts were glad to hear he’s on the case. Recently, Rao and a collaborator proved a different result about nonperiodic tilings of Wang tiles — squares whose colored edges can only be placed side by side if the colors match. Previous work had demonstrated that collections of Wang tiles exist that only give rise to nonperiodic tilings. “The first one that was found had over 20,000 tiles in it,” Mann said. “That later got reduced to 14. Rao proved that you can do it with 11 tiles and that’s the minimum. So he kind of knocked that problem out of consideration, too. He’s on a tear.”
This article was updated on July 12, 2017, to clarify Michaël Rao’s university affiliation, and again on July 13 to make clear that an einstein tile can only tile the plane nonperiodically.