The (Math) Problem With Pentagons

BIG MOUTH for Quanta Magazine
Introduction
Children’s blocks lie scattered on the floor. You start playing with them — squares, rectangles, triangles and hexagons — moving them around, flipping them over, seeing how they fit together. You feel a primal satisfaction from arranging these shapes into a perfect pattern, an experience you’ve probably enjoyed many times. But of all the blocks designed to lie flat on a table or floor, have you ever seen any shaped like pentagons?
People have been studying how to fit shapes together to make toys, floors, walls and art — and to understand the mathematics behind such patterns — for thousands of years. But it was only this year that we finally settled the question of how five-sided polygons “tile the plane.” Why did pentagons pose such a big problem for so long?
To understand the problem with pentagons, let’s start with one of the simplest and most elegant of geometric structures: the regular tilings of the plane. These are arrangements of regular polygons that cover flat space entirely and perfectly, with no overlap and no gaps. Here are the familiar triangular, square and hexagonal tilings. We find them in floors, walls and honeycombs, and we use them to pack, organize and build things more efficiently.
These are the easiest tilings of the plane. They are “monohedral,” in that they consist of only one type of polygonal tile; they are “edge-to-edge,” meaning that corners of the polygons always match up with other corners; and they are “regular,” because the one tile being used repeatedly is a regular polygon whose side lengths are all the same, as are its interior angles. Our examples above use equilateral triangles (regular triangles), squares (regular quadrilaterals) and regular hexagons.
Remarkably, these three examples are the only regular, edge-to-edge, monohedral tilings of the plane: No other regular polygon will work. Mathematicians say that no other regular polygon “admits” a monohedral, edge-to-edge tiling of the plane. And this far-reaching result is actually quite easy to establish using only two simple geometric facts.
First, there’s the fact that in a polygon with n sides, where n must be at least 3, the sum of an n-gon’s interior angles, measured in degrees, is
$latex S_n = 180(n – 2)$
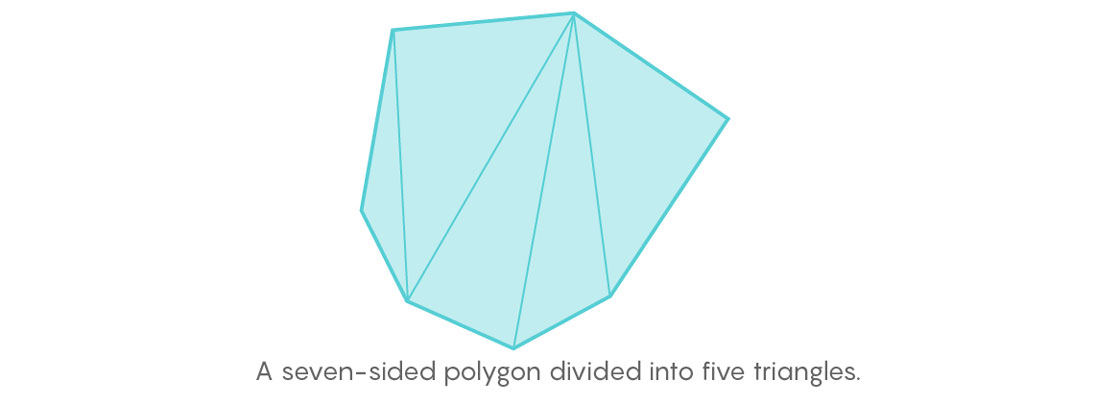
This is true for any polygon with n sides, regular or not, and it follows from the fact that an n-sided polygon can be divided into (n − 2) triangles, and the sum of the measures of the interior angles of each of those (n − 2) triangles is 180 degrees.
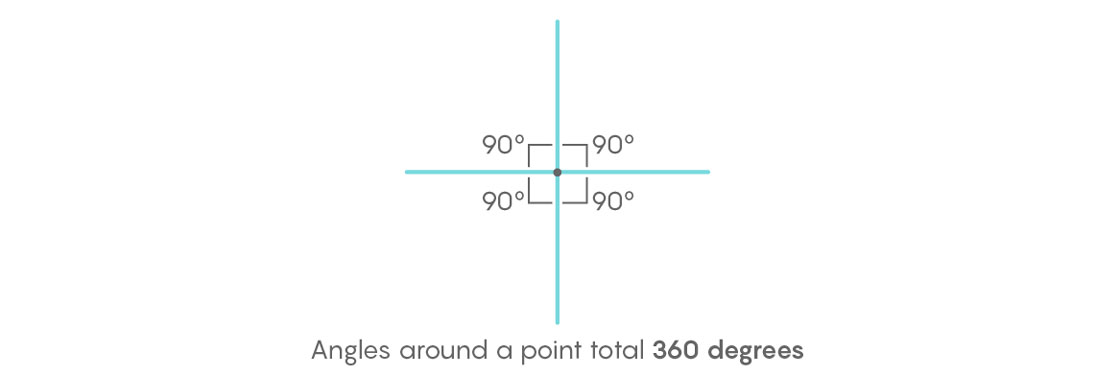
Second, we observe that the angle measure of a complete trip around any point is 360 degrees. This is something we can see when perpendicular lines intersect, since 90 + 90 + 90 + 90 = 360.
What do these two facts have to do with the tiling of regular polygons? By definition, the interior angles of a regular polygon are all equal, and since we know the number of angles (n) and their sum (180(n − 2)), we can just divide to compute the measure of each individual angle.
$latex \theta_n = \frac {180(n-2)}{n}$
We can make a chart for the measure of an interior angle in regular n-gons. Here they are up to n = 8, the regular octagon.
| n | Name | Sum of interior angles | One interior angle |
| 3 | Equilateral triangle | 180 | 60 |
| 4 | Square | 360 | 90 |
| 5 | Pentagon | 540 | 108 |
| 6 | Hexagon | 720 | 120 |
| 7 | Heptagon | 900 | $latex 128 \frac {4}{7}$ |
| 8 | Octagon | 1080 | 135 |
This chart raises all sorts of interesting mathematical questions, but for now we just want to know what happens when we try to put a bunch of the same n-gons together at a point.
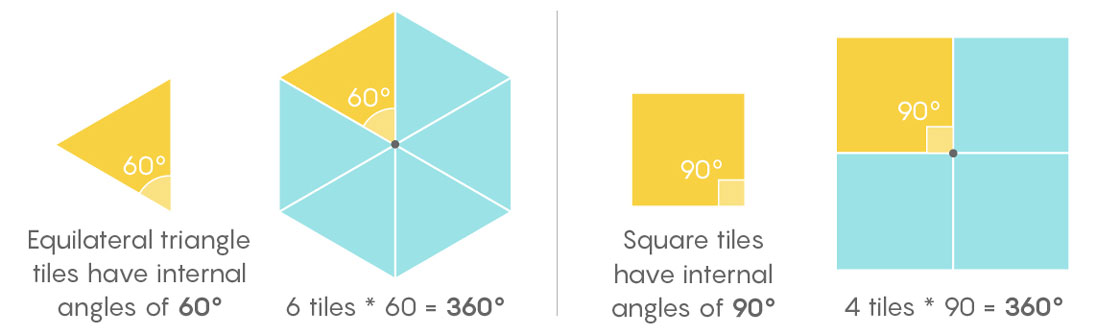
For the equilateral-triangle tiling, we see six triangles coming together at each vertex. This works out perfectly: The measure of each internal angle of an equilateral triangle is 60 degrees, and 6 × 60 = 360, which is exactly what we need around a single point. Similarly for squares: Four squares around a single point at 90 degrees each gives us 4 × 90 = 360.
But starting with pentagons, we run into problems. Three pentagons at a vertex gives us 324 degrees, which leaves a gap of 36 degrees that is too small to fill with another pentagon. And four pentagons at a point produces unwanted overlap.
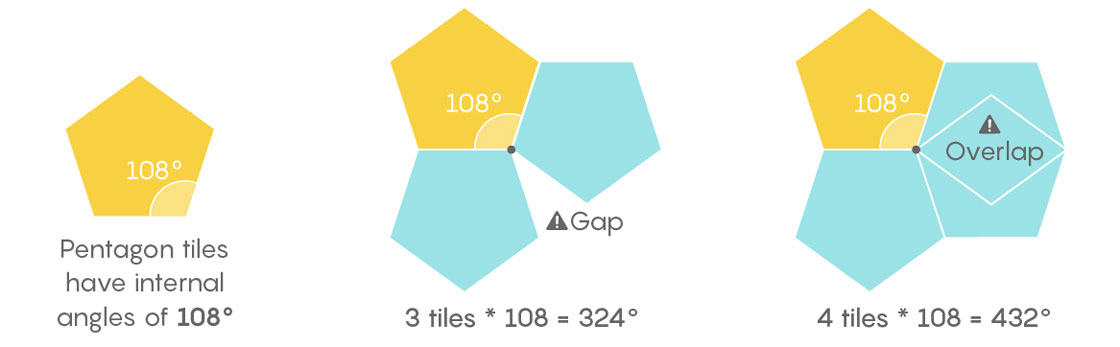
No matter how we arrange them, we’ll never get pentagons to snugly match up around a vertex with no gap and no overlap. This means the regular pentagon admits no monohedral, edge-to-edge tiling of the plane.
A similar argument will show that after the hexagon — whose 120-degree angles neatly fill 360 degrees — no other regular polygon will work: The angles at each vertex simply won’t add up to 360 as required. And with that, the regular, monohedral, edge-to-edge tilings of the plane are completely understood.
Of course, that’s never enough for mathematicians. Once a specific problem is solved, we start to relax the conditions. For example, what if we don’t restrict ourselves to regular polygonal tiles? We’ll stick with “convex” polygons, those whose interior angles are each less than 180 degrees, and we’ll allow ourselves to move them around, rotate them and flip them over. But we won’t assume the side lengths and interior angles are all the same. Under what circumstances could such polygons tile the plane?
For triangles and quadrilaterals, the answer is, remarkably, always! We can rotate any triangle 180 degrees about the midpoint of one of its sides to make a parallelogram, which tiles easily.

A similar strategy works for any quadrilateral: Simply rotate the quadrilateral 180 degrees around the midpoint of each of its four sides. Repeating this process builds a legitimate tiling of the plane.
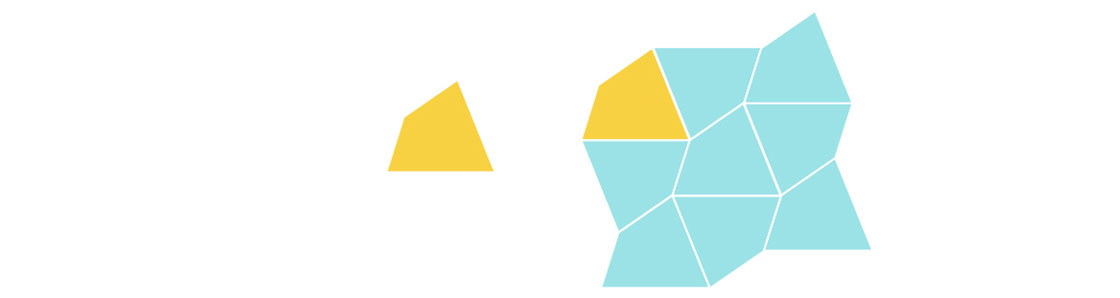
Thus, all triangles and quadrilaterals — even irregular ones — admit an edge-to-edge monohedral tiling of the plane.
But with irregular pentagons, things aren’t so simple. Our experience with irregular triangles and quadrilaterals might seem to give cause for hope, but it’s easy to construct an irregular, convex pentagon that does not admit an edge-to-edge monohedral tiling of the plane.
For example, consider the pentagon below, whose interior angles measure 100, 100, 100, 100 and 140 degrees. (It may not be obvious that such a pentagon can exist, but as long as we don’t put any restrictions on the side lengths, we can construct a pentagon from any five angles whose measures sum to 540 degrees.)
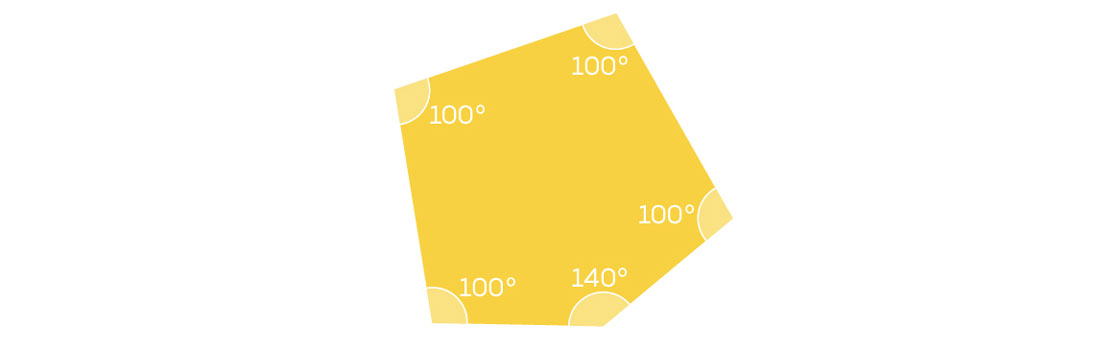
The pentagon above admits no monohedral, edge-to-edge tiling of the plane. To prove this, we need only consider how multiple copies of this pentagon could possibly be arranged at a vertex. We know that at each vertex in our tiling the measures of the angles must sum to 360 degrees. But it’s impossible to put 100-degree angles and 140-degrees angles together to make 360 degrees: You can’t add 100s and 140s together to get exactly 360.
| Angle Combinations | Deficit |
| 140 + 140 = 280 | 80 |
| 140 + 100 + 100 = 340 | 20 |
| 100 + 100 + 100 = 300 | 60 |
No matter how we try to put these pentagonal tiles together, we’ll always end up with a gap smaller than an available angle. Constructing an irregular pentagon in this way shows us why not all irregular pentagons can tile the plane: There are certain restrictions on the angles that not all pentagons satisfy.
But even having a set of five angles that can form combinations that add up to 360 degrees is not enough to guarantee that a given pentagon can tile the plane. Consider the pentagon below.
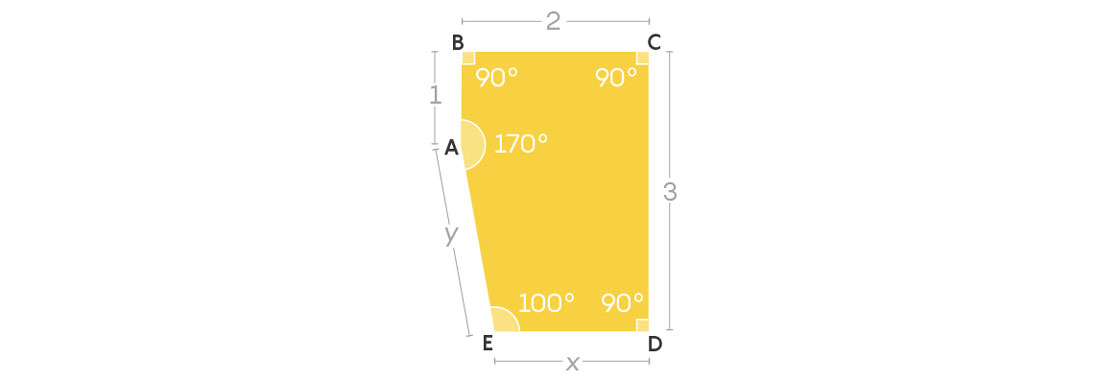
This pentagon has been constructed to have angles of 90, 90, 90, 100 and 170 degrees. Notice that every angle can be combined with others in some way to make 360 degrees: 170 + 100 + 90 = 360 and 90 + 90 + 90 + 90 = 360.
The sides have also been constructed in a particular way: the lengths of AB, BC, CD, DE and EA are 1, 2, 3, x and y, respectively. We can calculate x and y, but it’s enough to know that they’re messy irrational numbers and they’re not equal to 1, 2 or 3, or to each other. This means that when we attempt to create an edge-to-edge tiling of the plane, every side of this pentagon has only one possible match from another tile.
Knowing this, we can quickly determine that this pentagon admits no edge-to-edge tiling of the plane. Consider the side of length 1. Here are the only two possible ways of matching up two such pentagons on that side.

The first creates a gap of 20 degrees, which can never be filled. The second creates a 100-degree gap. We do have a 100-degree angle to work with, but because of the edge restriction on the y side, we have only two options.
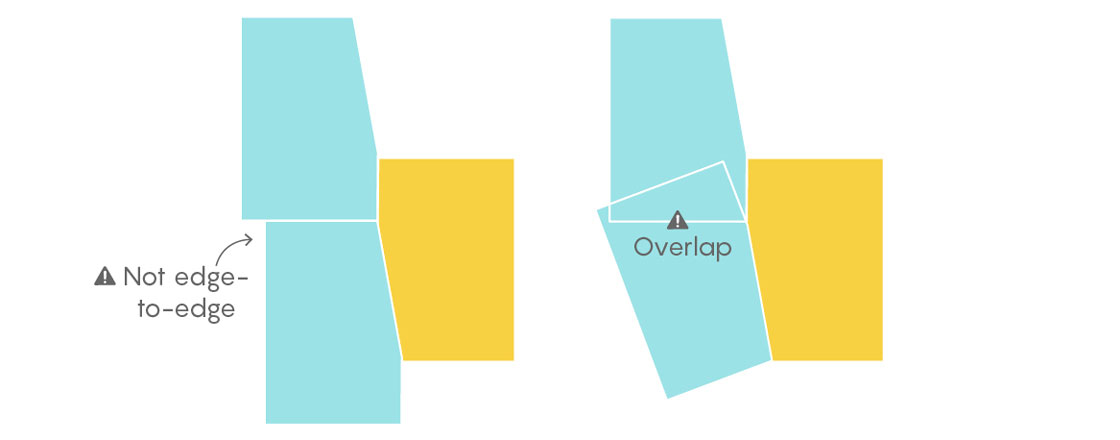
Neither of these arrangements generates valid edge-to-edge tilings. Thus, this particular pentagon cannot be used in an edge-to-edge tiling of the plane.
We’re starting to see that complicated relationships among the angles and sides make monohedral, edge-to-edge tilings with pentagons particularly complex. We need five angles, each of which can combine with copies of itself and the others to sum to 360. But we also need five sides that will fit together with those angles. Further complicating matters, a pentagon’s sides and angles aren’t independent: Setting restrictions on the angles creates restrictions for the side lengths, and vice versa. With triangles and quadrilaterals everything always fits, but when it comes to pentagons, it’s a balancing act to get everything to work out just right.
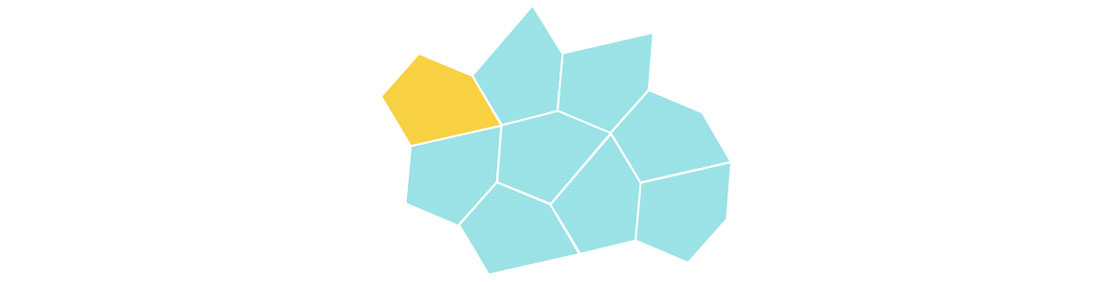
But some just-right pentagons exist. Here’s an example discovered by Marjorie Rice in the 1970s.

Rice’s pentagon admits an edge-to-edge tiling of the plane.
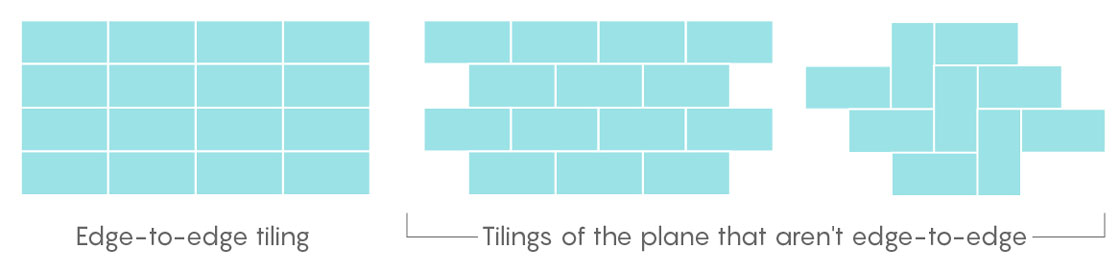
Things get trickier as we relax more conditions. When we remove the edge-to-edge restriction, we open up a whole new world of tilings. For example, a simple 2-by-1 rectangle only admits one edge-to-edge tiling of the plane, but it admits infinitely many tilings of the plane that aren’t edge-to-edge!
With pentagons, this adds another dimension of complexity to the already complex problem of finding the right combination of sides and angles. That’s partly why it took 100 years, multiple contributors and, in the end, an exhaustive computer search to settle the question. The 15 types of convex pentagons that admit tilings (not all edge-to-edge) of the plane were discovered by Karl Reinhardt in 1918, Richard Kershner in 1968, Richard James in 1975, Marjorie Rice in 1977, Rolf Stein in 1985, and Casey Mann, Jennifer McLoud-Mann and David Von Derau in 2015. And it took another mathematician in 2017, Michaël Rao, to computationally verify that no other such pentagons could work. Together with other existing knowledge, like the fact that no convex polygon with more than six sides can tile the plane, this finally settled an important question in the mathematical study of tilings.
When it comes to tiling the plane, pentagons occupy an area between the inevitable and the impossible. Having five angles means the average angle will be small enough to give the pentagon a chance at a perfect fit, but it also means that enough mismatches among the sides could exist to prevent it. The simple pentagon shows us that, even after thousands of years, questions about tilings still excite, inspire and astound us. And with many open questions remaining in the field of mathematical tilings — like the search for a hypothetical concave “einstein” shape that can only tile the plane nonperiodically — we’ll probably be putting the pieces together for a long time to come.
Download the “Math Problem With Pentagons” PDF worksheet to practice the concepts and to share with students.
This article was reprinted on Wired.com and in Spanish at Investigacionyciencia.es.









