What's up in
Quantized Columns
Latest Articles
How a NASA Probe Solved a Scorching Solar Mystery
The outer layers of the sun’s atmosphere are a blistering million degrees hotter than its surface. The hidden culprit? Magnetic activity.
Math That Connects Where We’re Going to Where We’ve Been
Recursion builds bridges between ideas from across different math classes and illustrates the power of creative mathematical thinking.
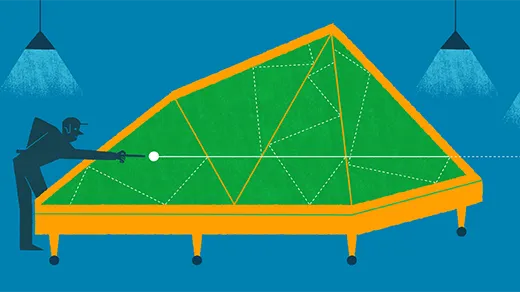
Unfolding the Mysteries of Polygonal Billiards
The surprisingly subtle geometry of a familiar game shows how quickly math gets complicated.
The Surprisingly Simple Math Behind Puzzling Matchups
If Anna beats Benji in a game and Benji beats Carl, will Anna beat Carl?
The Brain Region That Controls Movement Also Guides Feelings
The cerebellum is responsible for far more than coordinating movement. New techniques reveal that it is, in fact, a hub of sensory and emotional processing in the brain.
The New Quest to Control Evolution
Modern scientists aren’t content with predicting how life evolves. They want to shape it.
Pierre de Fermat’s Link to a High School Student’s Prime Math Proof
How Fermat’s less famous "little theorem" got mathematicians young and old to play with prime-like Carmichael numbers.
A Brief History of Tricky Mathematical Tiling
The discovery earlier this year of the “hat” tile marked the culmination of hundreds of years of work into tiles and their symmetries.
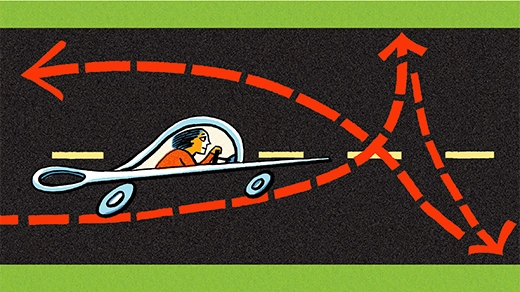
How Simple Math Moves the Needle
The spatial intuition behind a three-point turn offers an on-ramp to a century-old geometry problem.