Unfolding the Mysteries of Polygonal Billiards
James O’Brien for Quanta Magazine
Introduction
In Disney’s 1959 film Donald in Mathmagic Land, Donald Duck, inspired by the narrator’s descriptions of the geometry of billiards, energetically strikes the cue ball, sending it ricocheting around the table before it finally hits the intended balls. Donald asks, “How do you like that for mathematics?”
Because rectangular billiard tables have four walls meeting at right angles, billiard trajectories like Donald’s are predictable and well understood — even if they’re difficult to carry out in practice. However, research mathematicians still cannot answer basic questions about the possible trajectories of billiard balls on tables in the shape of other polygons (shapes with flat sides). Even triangles, the simplest of polygons, still hold mysteries.
Is it always possible to hit a ball so that it returns to its starting point traveling in the same direction, creating a so-called periodic orbit? Nobody knows. For other, more complicated shapes, it’s unknown whether it’s possible to hit the ball from any point on the table to any other point on the table.
Although these questions seem to fit snugly within the confines of geometry as it’s taught in high school, attempts to solve them have required some of the world’s foremost mathematicians to bring in ideas from disparate fields including dynamical systems, topology and differential geometry. As with any great mathematics problem, work on these problems has created new mathematics and has fed back into and advanced knowledge in those other fields. Yet despite all this effort, and the insight modern computers have brought to bear, these seemingly straightforward problems stubbornly resist resolution.
Here’s what mathematicians have learned about billiards since Donald Duck’s epically tangled shot.
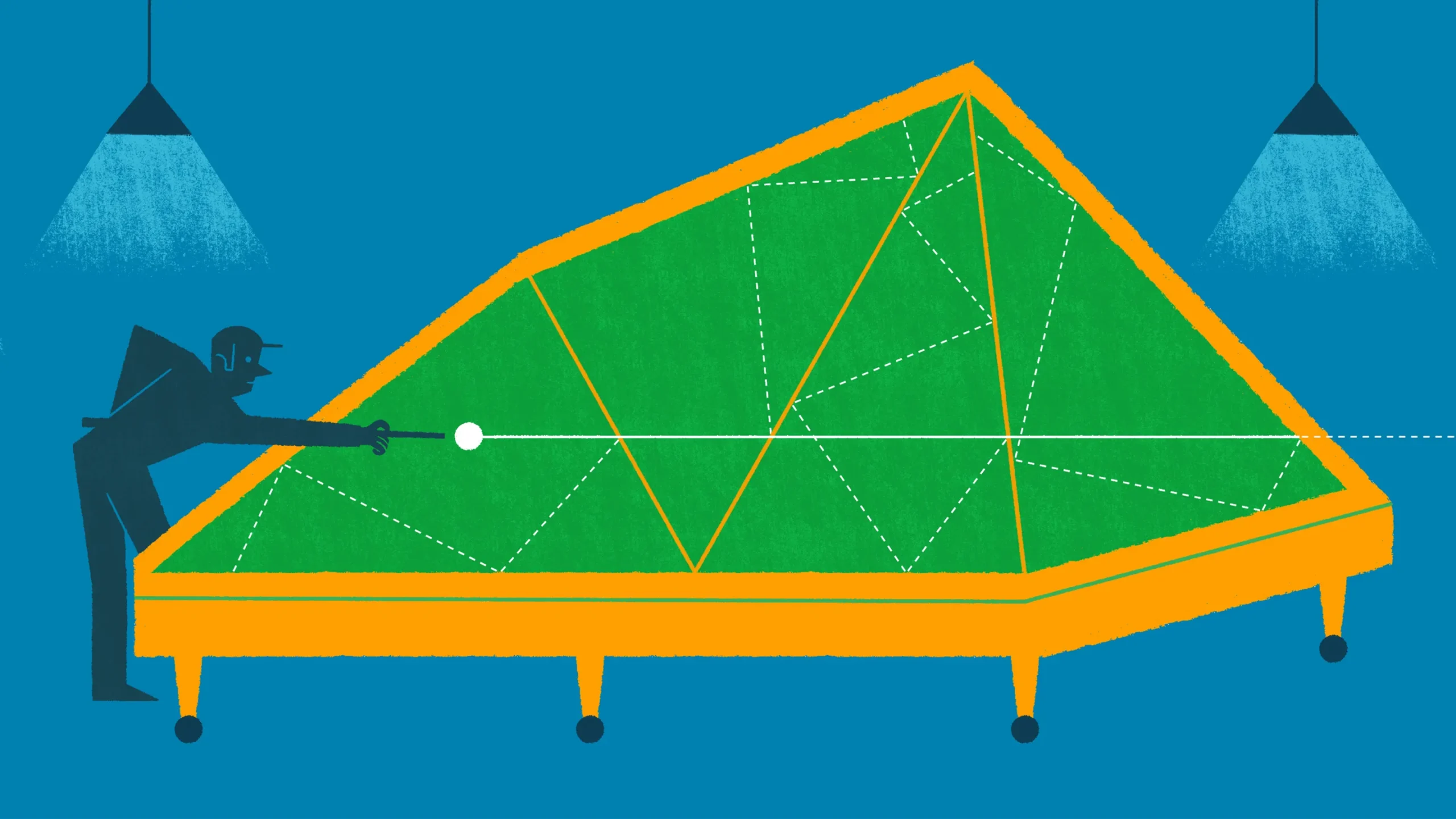
They typically assume that their billiard ball is an infinitely small, dimensionless point and that it bounces off the walls with perfect symmetry, departing at the same angle as it arrives, as seen below.
Without friction, the ball travels indefinitely unless it reaches a corner, which stops the ball like a pocket. The reason billiards is so difficult to analyze mathematically is that two nearly identical shots landing on either side of a corner can have wildly diverging trajectories.
A key method for analyzing polygonal billiards is not to think of the ball as bouncing off the table’s edge, but instead to imagine that every time the ball hits a wall, it keeps on traveling into a fresh copy of the table that is flipped over its edge, producing a mirror image. This process (seen below), called the unfolding of the billiard path, allows the ball to continue in a straight-line trajectory. By folding the imagined tables back on their neighbors, you can recover the actual trajectory of the ball. This mathematical trick makes it possible to prove things about the trajectory that would otherwise be challenging to see.
For example, it can be used to show why simple rectangular tables have infinitely many periodic trajectories through every point. A similar argument holds for any rectangle, but for concreteness, imagine a table that’s twice as wide as it is long.
Suppose you want to find a periodic orbit that crosses the table n times in the long direction and m times in the short direction. Since each mirror image of the rectangle corresponds to the ball bouncing off a wall, for the ball to return to its starting point traveling in the same direction, its trajectory must cross the table an even number of times in both directions. So m and n must be even. Lay out a grid of identical rectangles, each viewed as a mirror image of its neighbors. Draw a line segment from a point on the original table to the identical point on a copy n tables away in the long direction and m tables away in the short direction. Adjust the original point slightly if the path passes through a corner. Here’s an example where n = 2 and m = 6. When folded back up, the path produces a periodic trajectory, as shown in the green rectangle.
A Triangle Inequality
Billiards in triangles, which do not have the nice right-angled geometry of rectangles, is more complicated. As you might remember from high school geometry, there are several kinds of triangles: acute triangles, where all three internal angles are less than 90 degrees; right triangles, which have a 90-degree angle; and obtuse triangles, which have one angle that is more than 90 degrees.
Billiard tables shaped like acute and right triangles have periodic trajectories. But no one knows if the same is true for obtuse triangles.
To find a periodic trajectory in an acute triangle, draw a perpendicular line from each vertex to the opposite side, as seen to the left, below. Join the points where the right angles occur to form a triangle, as seen on the right.
This inscribed triangle is a periodic billiard trajectory called the Fagnano orbit, named for Giovanni Fagnano, who in 1775 showed that this triangle has the smallest perimeter of all inscribed triangles.
In the early 1990s, Fred Holt at the University of Washington and Gregory Galperin and his collaborators at Moscow State University independently showed that every right triangle has periodic orbits. One simple way to show this is to reflect the triangle about one leg and then the other, as shown below.
Start with a trajectory that’s at a right angle to the hypotenuse (the long side of the triangle). The hypotenuse and its second reflection are parallel, so a perpendicular line segment joining them corresponds to a trajectory that will bounce back and forth forever: The ball departs the hypotenuse at a right angle, bounces off both legs, returns to the hypotenuse at a right angle, and then retraces its route.
But obtuse triangles remain a mystery. In their 1992 paper, Galperin and his collaborators came up with a variety of methods of reflecting obtuse triangles in a way that lets you create periodic orbits, but the methods only worked for some special cases. Then, in 2008, Richard Schwartz at Brown University showed that all obtuse triangles with angles of 100 degrees or less contain a periodic trajectory. His approach involved breaking the problem down into multiple cases and verifying each case using traditional mathematics and computer assistance. In 2018, Jacob Garber, Boyan Marinov, Kenneth Moore and George Tokarsky at the University of Alberta extended this threshold to 112.3 degrees. (Tokarsky and Marinov had spent more than a decade chasing this goal.)
A Topological Turn
Another approach has been used to show that if all the angles are rational — that is, they can be expressed as fractions — obtuse triangles with even bigger angles must have periodic trajectories. Instead of just copying a polygon on a flat plane, this approach maps copies of polygons onto topological surfaces, doughnuts with one or more holes in them.
If you reflect a rectangle over its short side, and then reflect both rectangles over their longest side, making four versions of the original rectangle, and then glue the top and bottom together and the left and right together, you will have made a doughnut, or torus, as shown below. Billiard trajectories on the table correspond to trajectories on the torus, and vice versa.
In a landmark 1986 article, Howard Masur used this technique to show that all polygonal tables with rational angles have periodic orbits. His approach worked not only for obtuse triangles, but for far more complicated shapes: Irregular 100-sided tables, say, or polygons whose walls zig and zag creating nooks and crannies, have periodic orbits, so long as the angles are rational.
Somewhat remarkably, the existence of one periodic orbit in a polygon implies the existence of infinitely many; shifting the trajectory by just a little bit will yield a family of related periodic trajectories.
The Illumination Problem
Shapes with nooks and crannies give rise to a related question. Rather than asking about trajectories that return to their starting point, this problem asks whether trajectories can visit every point on a given table. This is called the illumination problem because we can think about it by imagining a laser beam reflecting off mirrored walls enclosing the billiard table. We ask if, given two points on a particular table, you can always shine a laser (idealized as an infinitely thin ray of light) from one point to the other. To put it another way, if we placed a light bulb, which shines in all directions at once, at some point on the table, would it light up the whole room?
There have been two main lines of research into the problem: finding shapes that can’t be illuminated and proving that large classes of shapes can be. Whereas finding oddball shapes that can’t be illuminated can be done through a clever application of simple math, proving that a lot of shapes can be illuminated has only been possible through the use of heavy mathematical machinery.
In 1958, Roger Penrose, a mathematician who went on to win the 2020 Nobel Prize in Physics, found a curved table in which any point in one region couldn’t illuminate any point in another region. For decades, nobody could come up with a polygon that had the same property. But in 1995, Tokarsky used a simple fact about triangles to create a blockish 26-sided polygon with two points that are mutually inaccessible, shown below. That is, a laser beam shot from one point, regardless of its direction, cannot hit the other point.
The key idea that Tokarsky used when building his special table was that if a laser beam starts at one of the acute angles in a 45°-45°-90° triangle, it can never return to that corner.
His jagged table is made of 29 such triangles, arranged to make clever use of this fact. In 2019 Amit Wolecki, then a graduate student at Tel Aviv University, applied this same technique to produce a shape with 22 sides (shown below). It’s unknown if a shape with fewer sides exists.
Proving results in the other direction has been a lot harder. In 2014, Maryam Mirzakhani, a mathematician at Stanford University, became the first woman to win the Fields medal, math’s most prestigious award, for her work on the moduli spaces of Riemann surfaces — a sort of generalization of the doughnuts that Masur used to show that all polygonal tables with rational angles have periodic orbits. In 2016, Samuel Lelièvre of Paris-Saclay University, Thierry Monteil of the French National Center for Scientific Research and Barak Weiss of Tel Aviv University applied a number of Mirzakhani’s results to show that any point in a rational polygon illuminates all points except finitely many. There may be isolated dark spots (as in Tokarsky’s and Wolecki’s examples) but no dark regions as there are in the Penrose example, which has curved walls rather than straight ones. In Wolecki’s 2019 article, he strengthened this result by proving that there are only finitely many pairs of unilluminable points.
Sadly, Mirzakhani died in 2017 at age 40, after a struggle with cancer. Her work seemed far removed from trick shots in pool halls. And yet analyzing billiard trajectories shows how even the most abstract mathematics can connect to the world we live in.
Correction: February 16, 2024
This story originally said that 22 was the smallest number of sides a polygon containing two interior points that don’t illuminate one another could have. The story has been updated to reflect that though the smallest such polygon known to exist has 22 sides, it remains unknown if a smaller one can be constructed.



