The Fuzzball Fix for a Black Hole Paradox
In the late 18th century, the scientist John Michell pondered what would happen if a star were so massive, and its gravity so strong, that its escape velocity would be equivalent to the speed of light. He concluded that any emitted light would be redirected inward, rendering the star invisible. He called these hypothetical objects dark stars.
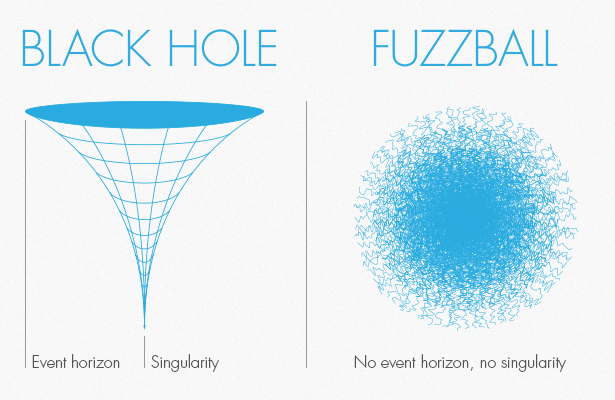
Michell’s 1784 treatise languished in quiet obscurity until it resurfaced in the 1970s. By then, theoretical physicists were well acquainted with black holes — the dark star idea translated into Albert Einstein’s theory of gravity. Black holes have a boundary called an event horizon that represents the point of no return, as well as a singularity, a point of infinite density within.
Yet Einstein’s description of the world is inconsistent with quantum mechanics, driving physicists to seek a complete theory of quantum gravity to reconcile the two. String theory is a leading contender, presenting yet another potential picture: Black holes may be reimagined as “fuzzballs,” with no singularity and no event horizon. Rather, the entire region within what was envisioned as the event horizon is a tangled ball of strings — those fundamental units of energy that string theory says vibrate in various complicated ways to give rise to space-time and all the forces and particles therein. Instead of an event horizon, a fuzzball has a “fuzzy” surface, more akin to that of a star or a planet.
Samir Mathur, a string theorist at Ohio State University, believes fuzzballs are the true quantum description of a black hole and has become a vocal champion of his own self-described “fuzzball conjecture” expanding on the concept. His version of fuzzballs provides potential mechanisms to resolve the knotty problem of reconciling the classical and quantum descriptions of a black hole — and, ultimately, the rest of our universe. But to make it work, physicists will have to abandon long-held notions of singularities and event horizons, a sacrifice many are unwilling to make.
Missing Entropy
Mathur’s work grew out of attempts to calculate the quantum properties of a black hole, as well as an ongoing struggle to resolve a paradox about what happens to information that falls into one. Both issues arise from Stephen Hawking’s insistence in the 1970s that black holes are not truly black. Due to quirks of quantum mechanics, they radiate a small amount of heat — called “Hawking radiation” — and thus have a temperature. If black holes have temperature, they must have entropy, often described as a measure of how much disorder is present in a given system. Every physical object has entropy, and entropy must always increase, per the second law of thermodynamics. Yet the smooth, featureless picture of a black hole described by general relativity doesn’t account for its entropy, which is a key feature of its quantum mechanical description.
An object’s entropy is described by microstates: the number of ways atoms can be rearranged to achieve the same macroscale object. A scrambled egg has more entropy than an unbroken egg because the scrambled egg’s atoms can be moved around in a seemingly infinite number of ways. By contrast, the distinct yolk and white in an unbroken egg limits the possibilities for atomic-level rearrangement.
Black holes are not exempted from the laws of thermodynamics. “Entropy comes from counting the [possible] states of atoms,” explained Joseph Polchinski, a physicist at the University of California, Santa Barbara. “So black holes should have some kind of atomic structure with countable states.” The problem is that any one black hole has far more possible states than thousands of scrambled eggs. The calculation required to measure entropy on that scale is truly daunting. It is possible to infer the number of states, however, using a formula devised by Jacob Bekenstein in 1972 that showed the entropy of a black hole to be proportional to the size of the event horizon around it.
By definition, we can’t see inside a black hole to count its possible states. But within the context of string theory, a black hole’s atomic structure comes in the form of strings and branes that, like atoms, can also be arranged in many different ways. We can imagine how strings might be arranged within a black hole such that the entropy would equal that found by Bekenstein’s formula.
Physicists must employ a variety of tunable toy models to perform those calculations. “There’s a ‘knob’ you can turn in string theory where the black hole is no longer black and you can see [strings and] branes inside,” said Polchinski. These gravity-free models make it possible to count the microstates. But once the gravity is turned back on, everything goes black again. Mathur’s fuzzball conjecture, by contrast, allows him to calculate the number of microstates in models that don’t exclude gravity.
In the view of Nick Warner, a string theorist at the University of Southern California, a fuzzball is less like a black hole than it is like a neutron star, an extra-dense state of matter that does not have a singularity or event horizon. Neutron stars owe their existence to the repulsive force produced when matter is squished together so tightly that the individual electrons are forced to occupy the same quantum state — something expressly forbidden in quantum mechanics.
String theory has a similar mechanism, said Warner, whereby massless fields provide the outward pressure instead of squashed electrons. Strings that fall onto the surface of a fuzzball combine to form larger, more-complex strings. Much as it is easier to pluck a long guitar string than a short one — because of the inherent tension — when strings join together to form longer strands, it is easier for them to expand to a wider diameter. They “puff up,” providing sufficient outward pressure to prevent a singularity. They “prevent the formation of a black hole by a phase transition to a new state of matter,” said Warner. By calculating the number of microstates in simple fuzzball models, it is possible to match the entropy as calculated by Bekenstein — a promising first step.
Even if Mathur is correct and his fuzzball conjecture can account for the missing entropy, this doesn’t resolve the knottier problem of the infamous black hole information paradox.
The Horizon Problem
Mathur’s fuzzball conjecture owes its evolution to his longstanding fascination with this paradox, another consequence of Hawking radiation. Hawking noted that according to quantum mechanics, even the vacuum of empty space is not truly empty. It pulses with energy from quantum fields, producing entangled pairs of virtual particles — matter and antimatter, or “Alice” and “Bob,” as they are commonly called in thought experiments. Virtual particle pairs are constantly popping into existence and then annihilating. But if such a virtual particle pair came into existence at the event horizon of a black hole, one half of the pair (Alice) could fall in before annihilation, leaving the other (Bob) outside. It would appear as if the black hole were emitting radiation.
As the Bob particles fly away, the overall mass of the black hole decreases. Given enough time it will wink out of existence. If this were to happen, the information formerly contained in the material that fell into the black hole would appear to vanish as well, violating the fundamental law of quantum mechanics that information must be conserved. Thus the laws of gravity predict a situation that seems to violate the laws of quantum mechanics. Physicists have fought over the paradox for 40 years. “It really laid down a gauntlet,” Polchinski said of Hawking’s original premise. “‘Quantum mechanics is modified. Find my mistake.’ And nobody found his mistake.”
Mathur boils the paradox down to two key elements. The first is general relativity’s insistence that the area of the event horizon is a vacuum, devoid of structure — or as John Wheeler once put it, “Black holes have no hair.” There are very good reasons to think so. Any dust, gas or elementary particle placed at the horizon should fall into the black hole, leaving the same vacuum state as before.
But this gives rise to the second element of the paradox: If there is a vacuum at the horizon, then there must be Hawking radiation, and a black hole will evaporate over time. “The minute you make a horizon, you’ve got the Hawking information problem,” said Warner. That is why Mathur argues that black holes must have hair after all. There must be structure at the horizon, because it provides a means of preserving information that falls into a black hole.
David Kaplan, Petr Stepanek and MK12 for Quanta Magazine; Music by Steven Gutheinz
Video: This two-minute video shows how black holes illuminate the apparent contradiction between general relativity and quantum mechanics.
Fuzzballs provide that structure. They aren’t empty pits, like traditional black holes. Rather, they are packed full of strings. They have a surface just like any other star or planet. And just like stars or planets, they emit heat in the form of radiation. When Mathur calculated the energy spectrum of the radiation emitted from a simple fuzzball, he found it exactly matched the prediction for Hawking radiation. In the fuzzball conjecture, then, the information paradox is an illusion: Information cannot be lost beyond the event horizon because there is no event horizon.
And while black holes are all alike, fuzzballs in Mathur’s thinking would be unique, making it possible — in theory at least — for physicists to trace a fuzzball back to the initial conditions that created it. As the fuzzball evaporates, the information inside it gets encoded in the Hawking radiation and carried away.
Fuzz or Fire?
Mathur’s insistence that there must be structure at the horizon did not meet with immediate acceptance. Three years later, however, Polchinski and three co-authors published a related thought experiment. The authors identified three central concepts in physics that could not all simultaneously be true around the event horizon of a black hole. One must be abandoned to resolve this so-called firewall paradox.
First, according to general relativity, Alice should notice nothing unusual as she crosses the event horizon of a black hole. Second, quantum mechanics demands that information must not be lost. Finally, the principle of locality requires that Alice may only be directly influenced by her immediate surroundings. Polchinski and his co-authors argued that in order to preserve both information and locality, the “no drama” condition must be sacrificed. At the event horizon there should be a ring of fire — the firewall.
The firewall paradox called attention to the possibility of structure at the event horizon — an irony not lost on string theorists like Warner. “We’ve been screaming that for about ten years now,” he said. He insists that the central firewall argument is fundamentally Mathur’s argument with a few extra flourishes: A firewall is essentially a hot fuzzball. “We’re not giving up on equivalence, we’re saying there is no singularity and no horizon. It just caps off into some fuzz,” he said. “The firewall is simply the fact that this stuff can be hot. I’m curious to see where the firewall story goes, because my view is it’s hot fuzzballs, and that’s the end of it.”
Polchinski freely admits that he and his co-authors didn’t initially recognize just how much their paper built on Mathur’s prior work; it has since been revised with proper credit given. But Polchinski said that the firewall paper makes the paradox more severe, crystallizing the issue in the most dramatic way.
General relativity holds that Alice will notice nothing unusual as she crosses the event horizon of a black hole; Polchinski and his co-authors posit she will burn up in a wall of fire as soon as she reaches it. So what happens if she falls into a fuzzball? Nobody knows for sure, but fuzzballs may not be as cuddly as they sound. Don Marolf, a physicist at the University of California, Santa Barbara, and one of the firewall paper’s co-authors, mused that Alice might be torn apart at the horizon or simply hit the fuzzball surface with a thud.
Or perhaps Alice would notice nothing amiss. In Mathur’s latest paper — posted to the scientific preprint site arxiv.org last week and not yet peer reviewed — he claims that an astronaut could be captured by a black hole, and she simply would not be able to tell, thanks to what he calls “fuzzball complementarity.” In Mathur’s scenario, black holes behave a bit like copy machines. Alice, who is made up of strings, hits the surface of the black hole. Her component strings combine with others to form longer strings that retain the characteristics of the original strings. An approximate copy of Alice’s strings gets made.
Moreover, the impact when she hits causes the fuzzy surface to vibrate. Mathur calculated the frequency spectrum of those vibrations and found that they were mathematically identical to what one would expect to see if Alice fell past the horizon of a black hole without noticing. Mathur likens it to how a grand piano and an electronic keyboard play the same notes despite their very different underlying mechanisms for producing sound. “The same set of phenomena are described by two apparently different things,” said Warner. So crashing into a fuzzball “might not be a whole hell of a lot different from just falling in [to a black hole].”
Many physicists remain skeptical of the fuzzball concept. Warner initially counted himself among them. “I did the good Galilean thing and got involved in the problem to kill it,” he admitted. Instead, he became a convert. He favors Mathur’s approach in part because it makes use of what physicists have learned from 30 years of string theory, rather than trying clumsily to patch together general relativity and quantum mechanics. “We’ve been trying to do that for 40 years,” he said. “It doesn’t work.”
But he acknowledges that the picture is incomplete. Fuzzballs match expected predictions in the context of toy models of highly idealized types of black holes with zero temperature. That means there is no Hawking radiation, and the black holes don’t evaporate, which is a critical component to retrieving information. Such models provide a mechanism for storing information by encoding the data in the fuzzball structure. But the information paradox is “both a storage and a recycling problem, and we don’t have the recycling mechanism,” said Warner. The next step will be to extend the concept to more realistic models that match the black holes we observe (indirectly) in our universe. “It’s not hopeless, it’s just daunting.”
Fuzzballs also require extra dimensions and rest on the assumption that string theory is the correct theory of quantum gravity, which may or may not be the case. Mathur still insists his fuzzball conjecture completes the information puzzle — at least in string theory — and by extension, the firewall paradox. Polchinski remains staunchly agnostic: “All bets are off; everything is open for discussion.” As for Marolf, he stands by the firewall, while conceding that it is not the only means of resolving the puzzle. “If Samir says he has a solution to the paradox, he is linguistically correct. He’s also in good company,” said Marolf. “There are lots of people with resolutions to the paradox. Whether it’s the way physics actually works in our universe remains to be seen.”
This article was reprinted on Wired.com.




