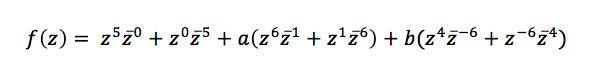Solution: ‘Creating Art With Mathematics’

Our Insights puzzle this month challenged Quanta readers to create pleasing symmetrical curves using mathematical expressions after solving a couple of problems, which were intended to help them divine the principles behind examples given by Frank Farris in his book Creating Symmetry: The Artful Mathematics of Wallpaper Patterns (Princeton University Press, 2015). As usual, our readers rose to the occasion, clearly explaining how the mathematics works to generate the symmetries, and then producing some breathtaking curves of their own.

Here are the questions and their solutions:

Question 1:

Look at the family of symmetrical curves below, one of which is featured in Farris’ book as a “mystery curve”:

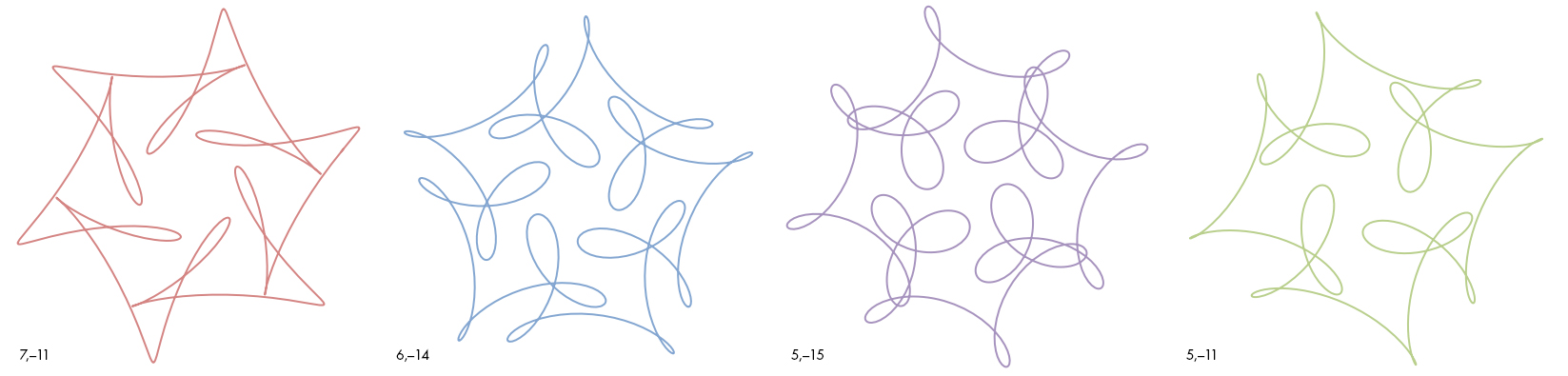
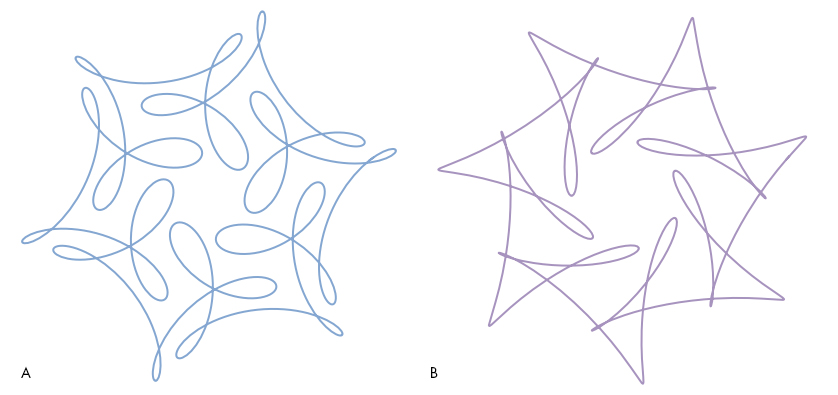
Each of these curves has an ordered pair of numbers associated with it, shown at the lower left of the curve. These two numbers determine the type of symmetry and complexity exhibited by the curve, and a simple mathematical relationship between the two numbers is required to generate the curve’s pleasant symmetry. In the second question below, we’ll give you the precise way these numbers are used to generate their curve. Without looking ahead, ponder these numbers and try to get an intuitive sense of how the curves change as the numbers do. Then look at curves A and B below and see if you can match them to the correct pairs of numbers, from the 10 choices given. Give your reasons for choosing your particular pairs and describe what you think the relationship is between the two numbers.

1. (5, –19)   2. (6, –19)   3. (7, –17)   4. (7, –12)   5. (7, –19)
6. (8, –20)   7. (8, –12)   8. (8, –13)   9. (8, –19)   10. (6, –24)

With careful observation it is not hard to establish a simple intuitive correlation between each curve and its pair of numbers, without any reference to the actual equations that generated them. From left to right, our example curves have sixfold, fivefold, fourfold and fourfold symmetry, while the first numbers associated with them are 7, 6, 5 and 5, respectively. This suggests that the first number is one greater than the degree of rotational symmetry. To figure out the role of the second number, look at the last two curves: Both exhibit fourfold symmetry, but the third curve is more complex internally than the fourth, with more looping. This correlates with a higher absolute value of the second number in the pair (–15 versus –11). The same correlation is seen in the first two curves as well. As for the relationship between the two numbers, notice that when you divide both numbers of each pair by the degree of symmetry, you get the same remainder, 1. In mathematical terms, both numbers are 1 modulo n, where n is the degree of symmetry

On the basis of these observations, let us tackle Question 1. Curve A has sixfold symmetry, so we expect the associated first number to be 7. The internal pattern is more complex than that of the first curve in the group of four, whose pair of numbers is (7, –11), so we would expect the second number to be somewhat larger in absolute value than 11. Of the three choices where the first number is 7, the only choice that follows the remainder rule is choice 3: (7, –17). Curve B has sevenfold symmetry (first number 8) with a not-too-complex internal pattern. The two choices that fit the remainder rule for a divisor of 7 are choice 6 (8, –20) and choice 8 (8, –13). The simpler internal pattern of Curve B, which resembles a sevenfold symmetrical version of the first curve (7, –11), suggests that the correct pair is choice 8: (8, –13).

[Update: The approximate method described above gives the right answer, but reader David Newall came up with a much more precise method that works for curves with simple parameters like these. If you count, you’ll find that a curve with parameters (m, n) has m–n loops or turning points. Curve B above has 21 loops and sevenfold symmetry so its parameters are (8, –13). Thank you, David.]

Question 2:

The “mystery curve” from Farris’ book is the second one (6, –14) from question 1. The curve has a fivefold symmetry. Here’s the expression that generated this curve: (cos(t) + cos(6t)/2 + sin(14t)/3, sin(t) + sin(6t)/2 + cos(14t)/3).

Note that this is a parametric equation — the first half gives the x-coordinate and the second part the y-coordinate as the parameter t goes from 0 to 2π. The mystery is this: What do the coefficients 6 and 14 have to do with generating fivefold symmetry? Why did we use –14 instead of 14 in question 1? Can you explain how this formula works to a general audience?

Readers Jason, Kyle Sinclair, Tom Nichols, Axel Gagge and others provided insightful explanations for why the numbers 6 and 14 generate fivefold symmetry. I can do no better than to quote Tom Nichols’ simple explanation for why the coefficient of the second term of the parametric expression given above is 6 and not 5:

You can think of each of the three terms as a vector that rotates around the complex plane like a hand on the clock. Like the hour hand, the first term rotates the slowest, making one completion as t goes from 0 to 2pi. Like the minute hand, the second term rotates faster, making 6 rotations as t goes from 0 to 2pi (in the case of the mystery curve). The third term goes the fastest and rotates 14 times around the complex plane in the same amount of time, but it rotates backwards.

To see why this results in 5-fold symmetry, think about the hands on a real clock. While the hour hand goes around once (in 12 hours), the minute hand goes around twelve times, but it only catches up with the hour hand 11 times in that 12-hour stretch, once at 1:05:27, again at 2:10:55 and so on up to 10:54:33 and finally 12 o’clock. That is, once in each hour except the first (from 12 to 1). So the hour and the minute hand line up 12 – 1 = 11 times over one full rotation of the hour hand resulting in an 11-fold symmetry of the positions of the hands on the clock.

We used –14 instead of 14 in the pair of numbers because, as Tom Nichols mentioned, the rotation caused by this term is backward: notice that the x part is a sine term and not a cosine term like the first two, and the y part is reversed as well. Without the minus sign, the numbers will not obey the remainder rule that we deduced in question one.

There is a deeper mathematical reason why the minus sign is appropriate, as Tom Nichols and Kyle Sinclair pointed out. A more natural representation of the curve which combines the x and y parts of the curve’s equations into a unified whole can be achieved using the complex-number plane. In this representation, the equation of the mystery curve is:

f(t) = e^it + (1/2)e^6it + (i/3)e^-14it
with the general form being  f(t) = e^it + (1/2)e^mit + (i/3)e^–nit

This equation can be used to generate a host of symmetrical curves. (Readers who are not familiar with complex exponentials may be forgiven for imagining that you need to go to MIT to understand the equation.)

Here’s Kyle Sinclair on how this gives rise to our remainder rule:

For an object to have k-fold symmetry, it must be invariant under rotations of 2pi/k radians. In other words, we want the following to be satisfied:

f(t + 2pi/k) = e^(2pi * i/k) * f(t).

Computing the left-hand side and using some facts about complex numbers, we see that our requirement is satisfied if and only if k divides both m – 1 and 1 – n.

In other words, when k (the degree of symmetry) divides the coefficients m and n, we need to get a remainder of 1. The mystery curve can be said to have fivefold symmetry of type one. You could also create symmetrical curves using different remainders such as 2, 3, etc., for all three terms, and these would be referred to as n-fold symmetries of type two, type three and so on. Kyle Sinclair’s “Engagement Ring,” as he called one of the curves he submitted for question 3, has fourfold symmetry of type three. As the numbers get larger, you may notice that our simple rules need to be modified or supplemented to predict the curves correctly. Can you find patterns in the numbers that enable you to intuitively predict the curves? Try it yourself and see!

Question 3 challenged readers to generate their own curves and share the best ones with us. Quanta readers responded magnificently, and we have published your images in the comments section of the original puzzle column. Thanks to Glenn, James M., Kyle Sinclair, Henry Lazarte, shivani, Girish Sharma, Charles Epperson, sudhir, Torsten Adair and Andrew Werth for sharing your creations and beautifying Quanta’s pages. Thanks also to Daniel Scher for creating a nifty online tool that allows you to change the coefficients using graphic sliders.

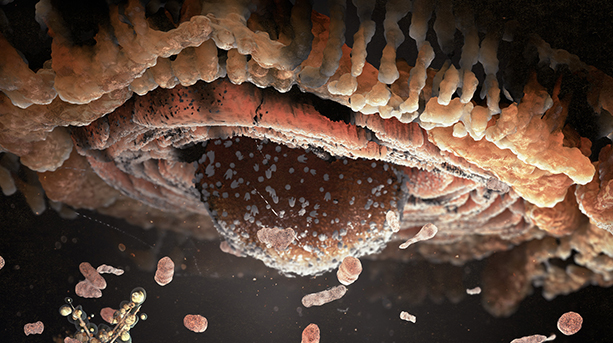
Of course, there is lot more that can be done mathematically to generate beauty. The illustration at the top of this column shows a rosette function generated by Farris, in which he used colors from a natural object, in this case a rhododendron. For readers who want to explore this further, the complex function that generated this beautiful illustration was:

where z and z-bar are complex conjugates and a and b are complex numbers chosen “for artistic effect.” Throughout his book, Farris uses this trick of creating his color wheel from photographs of a natural object to give his mathematical creations a beautiful realistic quality.

We know that such symmetrical figures are beautiful, but symmetry is also important to our understanding of the world, as David Kaplan explained in a video for Quanta, “How Does Symmetry Shape Nature’s Laws?” Why should something as visually beautiful and mathematically elegant as symmetry also be fundamentally important in the structure of the universe? As Einstein famously remarked, “The most incomprehensible thing about the universe is that it is comprehensible.” Why should it be so?

I am deeply fascinated by this question, and as I discussed in an article last year, I think it specifically relates to the cognitive-emotional link in our brains that has evolved to give us pleasure when we find the simplest explanations for complexity, both visually and in solving puzzles. When we encounter situations that require a lot of representational complexity in our brains, such as a disordered scene or a messy problem, we are programmed by evolution to try and make sense of them by finding patterns that make their representation more compact: In effect, we try to reduce a quantity I call “cognitive entropy.” Symmetry reduces the representational requirement of a visual object by finding regularities, triggering pleasurable reactions. Solving a puzzle does the same thing at the conceptual level. This characteristic is adaptive because the universe has evolved by self-assembly and natural selection, gradually growing more complex from simple beginnings. In such a process, the simplest mechanisms of complexity are encountered first and hence are the most probable. We conceptually run the process in reverse when we find simple explanations. In effect, a version of Occam’s razor — the problem-solving principle that states, “Among competing hypotheses, the one with the fewest assumptions should be selected” — is hard-wired into our brains and our senses. Hence, the patterns we find attractive are likely to correspond to the workings of the world.

Thank you all for sharing and contributing to our exploration of beauty in art and mathematics. The Quanta T-shirt this month goes to Kyle Sinclair, who gave great answers to the Insights questions and whose generated images were strikingly beautiful.