
Hiné Mizushima for Quanta Magazine
Introduction
If we could snap our fingers and change the way math and science are taught in U.S. schools, most of us would. The shortcomings of the current approach are clear. Subjects that are vibrant in the minds of experts become lifeless by the time they’re handed down to students. It’s not uncommon to hear kids in Algebra 2 ask, “When are we ever going to use this?” and for the teacher to reply, “Math teaches you how to think,” which is true — if only it were taught that way.
To say that this is now changing is to invite an eye roll. For a number of entrenched reasons, from the way teachers are trained to the difficulty of agreeing on what counts in each discipline, instruction in science and math is remarkably resistant to change.
That said, we’re riding the next big wave in K-12 science and math education in the United States. The main events are a pair of highly visible but often misunderstood documents — the Common Core math standards and the Next Generation Science Standards (NGSS) — that, if implemented successfully, will boldly remake the way math and science are taught. Both efforts seek to recast instruction in the fundamental ideas and perspectives that animate the two fields.
“What we did in reorganizing the content of school mathematics was long overdue,” said Phil Daro, one of three lead authors of the Common Core math standards.
The changes go beyond the contentious new methods of teaching arithmetic that have grabbed headlines and threatened to blunt the momentum of Common Core math. Both documents developed out of decades of academic research on how children learn, and they reflect similar priorities. They exhibit an elegant rethinking of the basic structure of knowledge, along with new assertions of what’s important for students to be able to do by the time they finish high school.
“Overall, there’s a movement towards more complex cognitive mathematics, there’s a movement towards the student being invited to act like a mathematician instead of passively taking in math and science,” said David Baker, a professor of sociology and education at Pennsylvania State University. “These are big trends and they’re quite revolutionary.”
Pedagogical revolutions are chancy endeavors, however. The Common Core math standards were released in 2010 and NGSS in 2013. Now, years on, even enthusiastic early adopters of the Common Core like the state of New York are retreating from the standards. While the ultimate impact of both the Common Core and NGSS is still uncertain, it’s clear these standards go beyond simply swapping one set of textbooks for another — to really take hold, they’ll require a fundamental rethinking of everything from assessments to classroom materials to the basic relationship between teachers and students.
The Old New Math
NGSS and the Common Core are a significant departure from the way science and math have been taught, but they didn’t come out of nowhere. In fact, they’re consistent with a trend that’s been slow-boiling for a half-century.
In a 2010 paper, Baker and colleagues analyzed 141 elementary school math textbooks published between 1900 and 2000. They found that what kids were learning changed considerably during that period. Until the 1960s, basic arithmetic accounted for 85 percent of math instruction. By the end of the century that proportion had dropped to 64 percent, with the balance of instruction devoted to more complex topics like advanced arithmetic and geometry.
“When you step back historically and sociologically, it’s clear education has really ratcheted up along these cognitive dimensions,” Baker said. “The idea that education is like men’s ties and just goes through this cycle of wide and thin is not true.”
Pedagogy has shifted as well. During the same period in which students began to learn more complex mathematics, leaders in science and math education launched complementary pushes to teach students to think more like real scientists and mathematicians. These efforts included the “New Math” of the 1960s and similar plans that decade to teach science as an “enquiry into enquiry,” as one leading expert of the time put it. Later manifestations of the impulse away from rote instruction include curricular standards created by the National Council of Teachers of Mathematics in the 1980s and the enthusiasm for “inquiry-based” science in the 1990s.
All of these initiatives had the right idea, but their implementation was off, say developers of NGSS and Common Core math. “Inquiry” is a habit of mind among scientists, but in the 1990s it was taught as its own curricular topic: Last week we learned about DNA, this week we’re going to learn about inquiry.
“Inquiry became almost an empty word, where it didn’t really matter what the inquiry was about,” said Heidi Schweingruber, director of the Board on Science Education at the National Academies of Sciences, Engineering, and Medicine, which provided guidance for the development of NGSS.
The same problem happened in math. For the last 50 years, reformers have wanted to teach kids to reason mathematically, to think nimbly about topics like quadratic equations that otherwise come off flat. Instead, in programs that employed the New Math, students often ended up playing logic games.
“The push toward conceptual understanding and understanding rich mathematical ideas sometimes ended in practice with students just engaged in activities and messing around,” said Robert Floden, dean of the College of Education at Michigan State University.
It’s not surprising that ambitious changes like these would be hard to implement. After all, teaching kids to adopt a scientific mindset is a subtler and more complex task than having them memorize the parts of a cell. For one thing, it requires teachers who inhabit that mindset themselves, and they’re harder to find. For another, it takes a more patient perspective than the prevailing one in public education, which expects teachers to post a learning objective on the board before each class and end every unit with a multiple-choice test.
Less Is More
How does one adjust the course of a curriculum that’s been gathering inertia for decades? The developers of NGSS and Common Core math started by reducing the mass of content that had accumulated over the years, often in haphazard fashion.
“Mainly, the U.S. mathematics curriculum prior to the Common Core was a geological accretion of additions, mostly, and [some] compressions over 50 years,” Daro said. “There was a lot of mathematical junk food and traveling down rabbit holes and up cul-de-sacs.”
Schweingruber made a similar point. “The U.S. has a mile-wide, inch-deep curriculum with tons and tons of things and ideas for kids to learn, but not an opportunity to go in depth,” she said.
As the authors got down to work on Common Core in 2009 and on NGSS a year later, some of their first discussions were about what to leave in and what to take out. “It required some argument on the part of folks in the framework about what that baseline really would look like,” Schweingruber said.
Lucy Reading-Ikkanda/Quanta Magazine
The final documents omitted a number of familiar topics. The NGSS writers eliminated instruction in the rote formula for stoichiometry calculations (the process for quantifying elements at different stages of a chemical reaction) from the high school chemistry curriculum. Daro and his collaborators on Common Core math, William McCallum of the University of Arizona and Jason Zimba of Student Achievement Partners, decided the technique of “simplifying” answers didn’t add much to mathematical understanding, so they took it out.
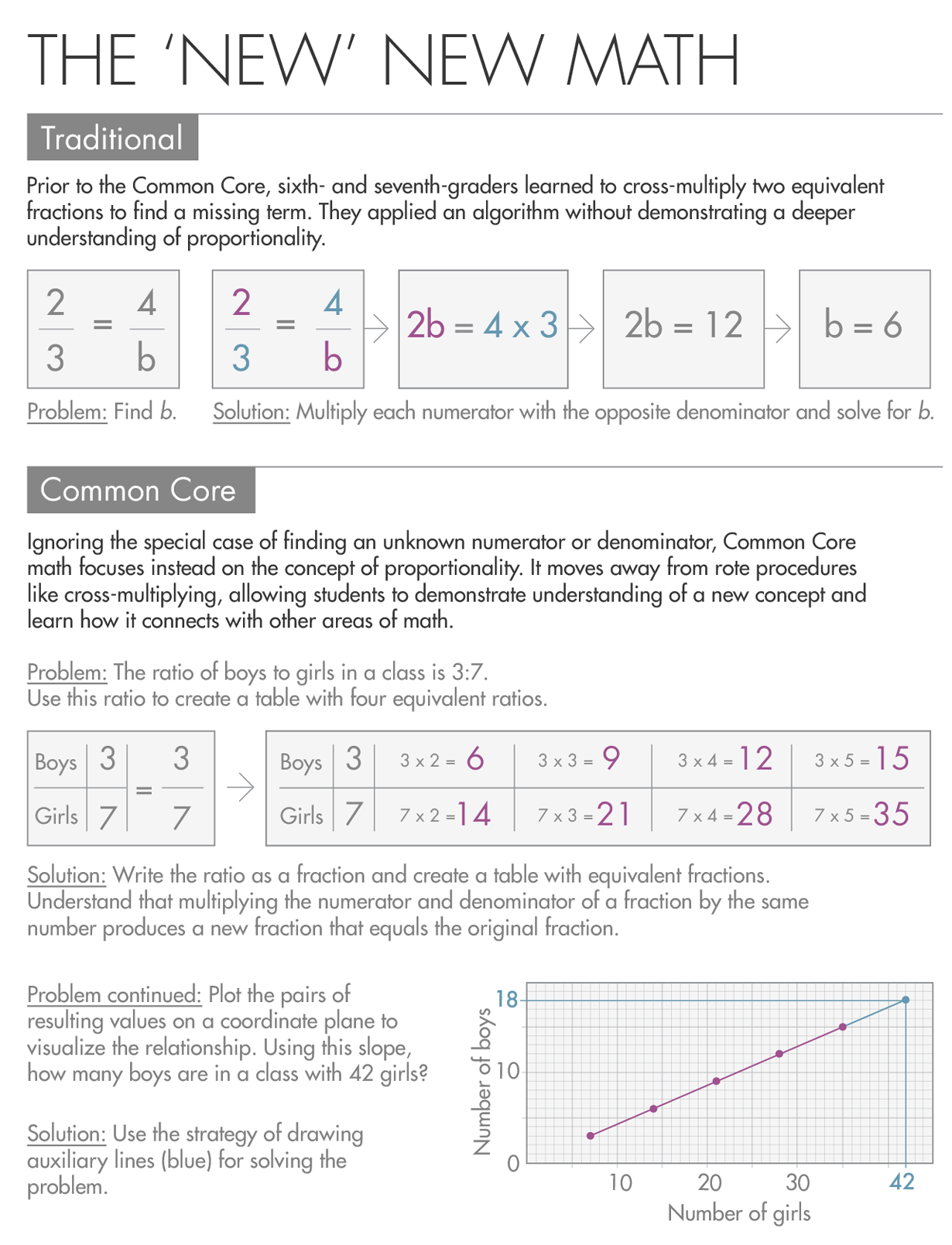
By removing content, the creators of Common Core math and NGSS hoped to expose core disciplinary ideas. A good example of this is how the Common Core teaches proportionality. Before, proportionality occupied about 10 percent of math instruction in grades six and seven. The main outcome of all that instructional time was that given two equivalent fractions, students could cross-multiply in order to find a missing term.
“What they’re learning is: The way you find the fourth number is by setting up this gadget called a proportion,” Daro said. “That’s not really learning anything about proportionality, that’s learning how to get answers to problems in this chapter.”
Common Core math doesn’t mention cross-multiplying, and it cuts out the special case of finding a missing fourth term. Instead, it focuses on the idea of a ratio, which begins modestly in sixth grade and develops all the way through calculus. Students begin by looking at a table of equivalent ratios — also presented as a double number line — and progress to the understanding that the slope of a line is a ratio.
“[The Common Core writers] said, look, let’s figure out what’s important about fractions and choose a path through them, which leads to ratio and proportion, which leads to linear functions, which leads to aspects of algebra,” said Alan Schoenfeld, a professor of education and mathematics at the University of California, Berkeley.
The understanding of slope as a ratio feeds into an even more fundamental emphasis in Common Core math: the analysis of functions. By thinking about the slope of a line as a ratio, students get in the habit of analyzing the parts of a linear function so they can see how changes in elements of the function affect the relationship between inputs and outputs.
Daro sees this shift from solving equations to analyzing functions as one of the biggest conceptual changes in the Common Core.
“The important line of progress is the line that begins with the theory of equations, a 19th-century central focus, to calculus and analysis, which is 20th-century [mathematics],” he said. “It’s a move from spending almost all your time solving equations towards analyzing functions.”
Stumbling Blocks
The change from solving equations to analyzing functions seems benign, but that has not stopped the Common Core from becoming a charged political issue. Currently 42 states plus the District of Columbia use the standards, with adoption motivated in part by financial incentives provided by the Obama administration’s Race to the Top initiative — a top-down tactic that has helped fuel blowback. There have been plenty of other complications, too, from parents complaining that they don’t know how to help their first-graders with their math homework, to concerns that the assessments that accompany the Common Core are too hard. As a result, even stalwart adopters are questioning whether the standards work. In December 2015, Governor Andrew Cuomo of New York announced that his state would undertake a “total reboot” of the Common Core math standards in the coming years.
The designers of NGSS, which came out three years after the Common Core without any kind of federal mandate, say they learned from the contentious rollout of the earlier standards. So far, 17 states plus the District of Columbia have adopted NGSS and 11 more states have implemented standards that are similar to varying degrees.
“The Common Core got people to sign on and implement standards before the standards were there, and I think that backfired,” Schweingruber said. “I feel like the intent of the standards is to improve what happens to kids in classrooms, and if that happens even before a state formally adopts, that’s fine with me.”
Still, NGSS has had its controversies. The document includes standards related to climate change and evolution, which has motivated opposition in conservative states. And, politics aside, the standards necessitate sweeping changes to the way science is taught.
Like Common Core math with its long-running development of core concepts, NGSS reframes science in terms of a small number of basic ideas that inform the scientific perspective. These include “structure and function,” “patterns,” “cause and effect,” “stability and change,” and “systems and systems models.”
“Even at a young age you’re going to have a workable knowledge of energy so you can apply it,” said Joseph Krajcik, a professor of science education at Michigan State and the lead author of the NGSS physical science standards. “At a third-grade level you might know that as something is moving, it has energy, and the faster it’s moving, the more it can do something. It’s a nascent idea of what energy is, and it builds across time.”
This slow-building approach is at odds with some aspects of public education. It’s not uncommon for districts to require that each class period address a discrete objective, and teachers are expected to measure whether students learned it at the end of the period. The authors of Common Core math and NGSS don’t see their disciplines fitting into that structure.
“One insight we got is that there’s almost no mathematics worth learning that breaks into lesson-size pieces,” Daro said. “You have a three- or four-week sequence and treat it with coherence. It’s about systems and structures, not small facts and small methods. It’s about how it all works together.”
Schweingruber agrees. “Some of these ideas in science are hard to get quickly,” she said. “It took humans hundreds of years, so why would kids figure them out quickly?”
The same mismatch between the standards and the way public education is set up occurs in another major area: assessments. Because standardized tests often drive instruction, it’s hard to expect teachers to teach differently unless students are tested differently.
“Teachers are starting to make changes in their classrooms,” Schweingruber said, “but if they’re still looking out toward a large-scale test their kids will have to take that is completely contrary to what they’re doing in the classroom, that can be problematic.”
There is progress in that direction. Two recent initiatives, the Partnership for Assessment of Readiness for College and Careers and the Smarter Balanced Assessment Consortium, are developing standardized tests that incorporate a greater variety of question types, like constructed response questions in which students are asked to explain their reasoning, and technology-enhanced questions in which, for example, students manipulate a line on a graph to make it match a given algebraic function.
“You’re seeing a deeper push for conceptual understanding and the ability to apply mathematics, and assessments are on their way to becoming equipped to actually assess that,” said Robert Kaplinsky, a math teaching specialist and consultant in Southern California.
The New Science
On the first and third Thursdays of every month, science teachers from around the country gather for #NGSSchat, a Twitter conversation about how to implement the new science. Topics for discussion have included how to incorporate reading and writing into science instruction and how to use technological tools alongside the standards. The July chats focused on “storylining,” which is emerging as a popular technique for bringing the standards to life in the classroom.
In a storyline, a teacher begins by introducing students to a phenomenon that prompts questions that students will investigate over the course of about two months. The question needs to be related to science, but accessible enough to grab students right away, and broad enough that it can’t be answered by a Google search. One storyline asks students to explain the biology behind the death of the Georgia high school football player Zyrees Oliver in 2014 after he drank too much fluid during practice. Another storyline asks simply: How does a seed grow into a tree?
“The storyline needs to be complex enough that it’s not going to just be a one-day or several-day event,” said Tricia Shelton, a high school science teacher in Kentucky and co-organizer of the NGSS chats who has been active in the implementation of NGSS. “It’s a necessity that it forces students to make those connections between many pieces of science in a coherent way.”
With storyline science, there are correct explanations, but there’s no right answer. A teacher’s job becomes less about handing down facts and more about establishing a classroom environment in which students can gather evidence and formulate arguments, with nudges along the way. This is a significant change from the way teachers have traditionally understood their role in the classroom. During the July 7 chat, some participants doubted their ability to make the shift. “[Teachers] are woefully unprepared [for] engaging in inquiry driven lessons. Local [teachers’] collaboration essential,” one contributor tweeted.
This concern is not lost on the NGSS developers.
“For some elementary teachers it will be like I’m doing science in a real way for the first time ever,” Schweingruber said. “For high school teachers I think one of the biggest shifts will be the emphasis on kids carrying out investigations and making decisions. That’s a real shift in your role as a teacher.”
Shelton thinks the instructional changes entailed by NGSS are too big to internalize in isolated chunks of professional development.
“Face-to-face learning is super essential, but you can’t get enough in one or two days,” she said. “You need some kind of sustained system to try things out in your own classroom and then a support network that you can go back to. Without that support I think it’s hard to make that big shift.”
Along with professional networks, teachers also need curricular materials that fit the NGSS approach — textbooks, assessments and lab equipment that are well-suited to the basic method of gathering evidence and building arguments. One classroom technique that has gained currency is the building and analysis of models — functions that tune an input with some number of parameters and produce an output that describes phenomena in the world. It’s sophisticated work more often performed by professional researchers than 10th-graders.
“The first time I constructed a model was in graduate school,” Krajcik said. “It’s very challenging to say to a kid: How would you explain how all the parts work together? That’s tough.”
Constructing models may be complicated, but it’s also a perfect way for students to learn how to bring together multiple forms of evidence in the service of a larger scientific argument. The Concord Consortium, an educational research organization based in Massachusetts, is currently working with Krajcik’s group at Michigan State to create a tool called SageModeler that, in its simplest form, lets students drag and drop icons to create conceptual models to explain real-world events.
“The SageModeler tool allows [students] to construct a representation of some phenomenon and test it out,” said Dan Damelin, co-creator of SageModeler. “They can see what are the results of my setting up this model of how I think things work.”
The first unit for the software, which will be pilot-tested in the spring, follows the storyline-style question: “Why Do Fishermen Need Forests?” It allows middle school students to investigate the causes and consequences of ocean acidification.
Prior to building an ocean acidification model, students will read about topics like deforestation, receive some direct instruction about the distinction between acids and bases, and carry out experiments that will give them a tangible sense of the factors involved. These could include exhaling into a jar of water containing a pH indicator (and observing that, as the water absorbs carbon dioxide, its pH declines) or conducting experiments to understand the role of photosynthesis in carbon sequestration.
Once the students have a feel for the factors contributing to ocean acidification, they’ll start to construct their models by pulling images from a clip art database to represent the variables they want to include: a car to represent carbon dioxide emissions, trees to represent carbon-dioxide-absorbing plants, shellfish to represent shellfish health, a fishing boat to represent the fishing economy. After students have defined relationships between the variables, they’ll run the model, graph the resulting data, and then refine their work to better approximate real-world data — in this case, data from the marine research center Station Aloha in Hawaii that can be dragged into SageModeler for a side-by-side comparison.
Teaching in this fashion can be exciting, but it will take sustained commitment for these techniques to ripple through the 100,000 or so public schools in the United States. In order for the new science and math standards to succeed, the entire education ecosystem will need to pull in that direction, from writers of standards to textbook publishers to professors in education schools to curriculum leaders running professional development sessions, to teachers swapping lesson ideas online. Just as the core concepts in math and science require repeated encounters over many years to be fully absorbed, a new practice of math and science teaching will need time to become established.
“I hope we give it the time,” Schweingruber said. “One problem in education reform is, people have unrealistic expectations about how quickly you change it. If you know it’s a huge ship, you have to give it some time before you decide it’s not working.”
Correction: This article was revised on October 5, 2016, to reflect that while Heidi Schweingruber co-directed a study that led to the framework that the Next Generation Science Standards are based on, she was not co-director of NGSS itself.
This article was reprinted on Wired.com.



