What Sonic Black Holes Say About Real Ones

In a 1972 lecture at the University of Oxford, a young physicist named William Unruh asked the audience to imagine a fish screaming as it plunges over a waterfall. The water falls so fast in this fictitious cascade that it exceeds the speed of sound at a certain point along the way. After the fish tumbles past this point, the water sweeps its screams downward faster than the sound waves can travel up, and the fish can no longer be heard by its friends in the river above.
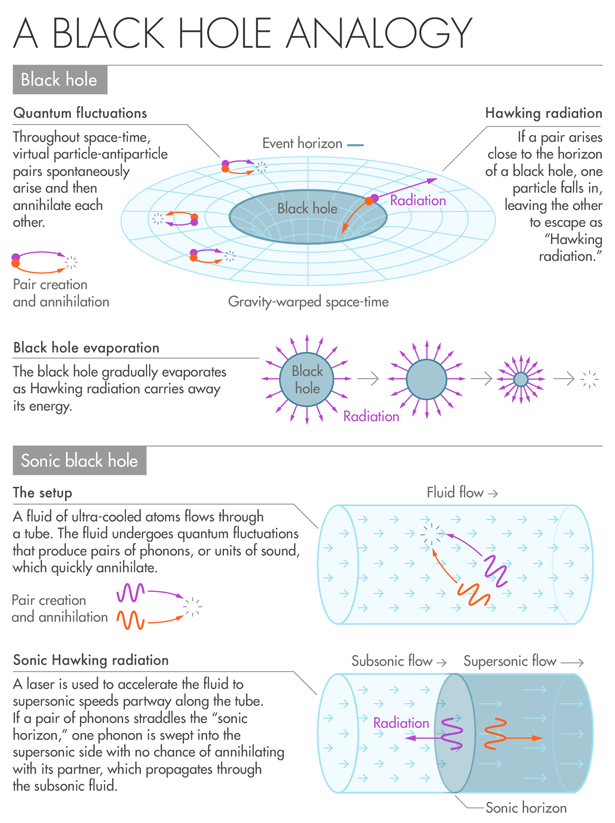
Something similar happens, Unruh explained, when you fall into a black hole. As you approach one of these super-dense objects, the fabric of space and time becomes increasingly curved — equivalent to strengthening gravity, according to Albert Einstein’s general theory of relativity. At a point of no return known as the “event horizon,” the space-time curvature becomes so steep that signals can no longer climb to the outside world. Within the event horizon, even light is held captive by the black hole’s gravity, rendering black holes invisible.
In the years following Unruh’s talk, black holes — places where general relativity and quantum mechanics, the two pillars of modern physics, meet and crumble in paradox — rose from obscurity to become leitmotifs in the quest for an all-encompassing theory of “quantum gravity.” Meanwhile, Unruh’s acoustic analogy turned out to work even better than he first thought. In a seminal 1981 paper, he showed that black hole event horizons and sonic horizons in systems like his waterfall — which are now referred to as sonic black holes — can be described by identical equations. Considering their “amazing mathematical similarities,” Unruh, a professor at the University of British Columbia in Vancouver, said recently, “you get the feeling that if you really understand one system, that will give you insight into the other.”
Researchers began plumbing the physics of sonic black holes for clues about actual black holes. And in recent years, they’ve started creating sonic black holes in the lab and devising increasingly sophisticated analogue experiments. This past summer, Jeff Steinhauer of the Technion in Haifa, Israel, reported the ultimate find: the detection of the sonic analogue of Hawking radiation, a hypothetical black hole phenomenon predicted by Stephen Hawking in 1974.
Hawking’s prediction that black holes radiate heat and eventually evaporate completely gives rise to the profound “information paradox,” which asks what happens to information about the stuff that fell into them. Hawking’s calculation suggests that this information is lost, essentially leaking out of the universe when it enters a black hole; in that case, the framework of quantum mechanics, which treats information as the universe’s fundamental, indestructible currency, must be abandoned. But if information is preserved, as most physicists believe, then Hawking’s prediction is wrong, and the task for any theory of quantum gravity is to reveal the flaw in his logic. The information paradox “has sharpened the challenge of what we need to confront to understand quantum gravity,” said Raphael Bousso, a theoretical physicist at the University of California, Berkeley, who was Hawking’s protégé.
For all its importance, Hawking’s calculation cannot be tested directly; the radiation from actual black holes is far too faint to detect. The measurement of the analogous effect in a sonic black hole — in this case, quantum units of sound radiating outward from a sonic horizon — therefore brings a long-standing question to a head: Are sonic black holes true analogues of black holes? More specifically, do Steinhauer’s findings indirectly validate Hawking’s calculation, proving that information is lost in black holes?
“Everybody in the community is saying, ‘Wow, great experiments!’” said Daniele Faccio, a physicist at Heriot-Watt University in Edinburgh, Scotland, who also studies analogue black holes. “But I think a lot of people are saying, ‘What do they mean?’”
Some researchers see indirect evidence for Hawking radiation in Steinhauer’s experiment. In a paper posted online last month, the physicist-turned-philosopher Karim Thebault of the University of Bristol in England argued that “an analogue black hole can be taken to ‘stand in’ for an astrophysical black hole.” Others see a red herring. Daniel Harlow, a theoretical physicist at Harvard University, deemed the experiment “an amusing feat of engineering” that “won’t teach us anything about black holes.”
The question of which interpretation is correct comes down to what, exactly, Hawking’s calculation 42 years ago revealed about the universe.
Surprisingly, he showed that black holes aren’t black; random quantum jitter makes them glow. Everywhere in space-time, pairs of “virtual” particles are constantly arising and mutually annihilating. Hawking realized that when these pairs arise straddling the horizon of a black hole, one virtual particle will get sucked in while its partner escapes, preventing their mutual destruction. The escaped particle becomes real, stealing the energy needed for the upgrade from the black hole’s gravitational field. Meanwhile the in-falling particle acquires negative energy, lowering the energy of the black hole. Thus, one radiated particle at a time, the black hole blinks out of existence, ultimately leaving no trace: Hawking’s calculation indicated that the radiation is “thermal,” consisting of a featureless, random spread of energies that encodes no details about the collapsed star that formed the black hole, or about anything else of interest that might have fallen in.
Therein lies the paradox. According to quantum mechanics, the probabilities of all possible states of particles in the universe must respect “unitarity,” evolving in such a way that the universe’s past states can in principle always be uniquely determined by rewinding from its present state. But if information is lost when a black hole evaporates into a featureless gas of Hawking radiation, then the universe’s past can’t be gleaned from the present, and quantum mechanics breaks down.
Or perhaps Hawking erred.
To do his calculation, he made a key assumption: that space-time is smooth and continuous at the horizon of a black hole, as described by general relativity. Physicists believe that this is an approximation; zoom in far enough on Einstein’s space-time continuum, and a more fundamental, quantum form of gravity emerges. But whereas quantum gravity surely becomes important near a black hole’s super-dense center, known as its “singularity,” Hawking assumed that he could gloss over this short-distance physics in his description of quantum fluctuations at the horizon, where gravity is comparatively mild. According to general relativity, the slope of space-time is gentle enough at the horizon of a typical supermassive black hole (like those at the centers of many galaxies) that an astronaut floating past it wouldn’t even notice.
In 1981, Unruh discovered that Hawking’s approximation scheme can also be applied to fluids. Like space-time, fluids appear continuous on large scales even though deep down they’re made of discrete atoms. Unruh showed that, just as pairs of particles fluctuate in and out of space-time, vibrations called “phonons,” the quantum units of sound, should surface throughout fluids. And when pairs of phonons arise near the sonic horizon of a sonic black hole, they should get wrenched apart and rendered permanent, producing the sonic analogue of Hawking radiation.
This is the phenomenon that Jeff Steinhauer reported in August in Nature Physics, after toiling over his experiment since 2009 — “exclusively, all day every day,” he said. He created an exotic fluid called a “Bose-Einstein condensate” out of super-cooled rubidium atoms. He then got it flowing, and zapped the fluid partway along its flow path with a laser, accelerating it to a supersonic speed and creating a sonic horizon. Finally, Steinhauer measured quantum entanglement between pairs of phonons on either side of this horizon, consistent with sonic Hawking radiation.
The finding confirms that the fluid approximation works in the case of sonic black holes. “The question is, how related are the approximations?” said Stephan Hartmann, a philosopher of physics at Ludwig Maximilian University in Munich, Germany. If sonic black holes serve as a true analogue, then Hawking’s approximation is correct, the event horizon is an uneventful place, and information gets destroyed in black holes, meaning that the probabilistic rules of quantum mechanics must be replaced by a more fundamental framework. If Hawking’s approximation is wrong, then sonic black holes are not good proxies for black holes, and quantum gravity might somehow encode black hole histories in their radiation, preserving information as black holes evaporate.
Unruh believes Hawking’s approximation is correct. In 2005, he and Ralf Schützhold of the University of Duisburg-Essen in Germany showed that Hawking radiation consistently came out as a robust theoretical prediction in both sonic black holes and actual black holes, no matter what theoretical assumptions they made about the details of the short-distance physics. The small-scale properties of space-time or fluids never affected the outcome of the calculation, suggesting that Hawking’s approximation wasn’t glossing over anything important. Unruh interprets this to mean that effects from quantum gravity aren’t capable of modifying Hawking radiation and rescuing information. In his opinion, Steinhauer’s result adds to the evidence that “this thermal radiation is a really robust phenomenon,” and thus, that “information is lost.”
However, most quantum gravity researchers believe that information is preserved — including Hawking, who switched camps in the 2000s. From their perspective, an analogue to Hawking radiation in sonic black holes says nothing about true black holes because the two are categorically different; whereas the fluid approximation is accurate in the case of sonic black holes, space-time must not be approximately smooth at black hole event horizons. Somehow, quantum gravity modifies horizons — and it must do so in an extreme way, to get around Unruh and Schutzhold’s argument about the robustness of Hawking radiation. “We are in the situation where something big has to give,” Bousso said. “But we still don’t know exactly what to replace general relativity with at the horizon.”
Some thought experiments suggest that black holes might be empty shells that carry all their information plastered on their horizons and project it outward to the rest of the universe like holograms. In that case, falling into a black hole would be less like a fish plunging over a waterfall and more like a bug going splat on a window.
In the majority opinion, the comparison with sonic black holes only reinforces how strange black holes and the theory of quantum gravity must be. Harlow, who takes this view, sees sonic black holes not as black hole analogues, but more like computer simulations that are running the wrong equations. If you were to simulate the equations of quantum gravity, “then I do expect you to find the right answer,” he said. “Currently, I don’t know which equations to give you.”
This article was reprinted on Wired.com.



