Latest Articles
How Tadayuki Watanabe Disproved a Major Conjecture About Spheres
Watanabe invented a new way of distinguishing shapes on his way to solving the last open case of the Smale conjecture, a central question in topology about symmetries of the sphere.
In Topology, When Are Two Shapes the Same?
As topologists seek to classify shapes, the effort hinges on how to define a manifold and what it means for two of them to be equivalent.
New Math Book Rescues Landmark Topology Proof
Michael Freedman’s momentous 1981 proof of the four-dimensional Poincaré conjecture was on the verge of being lost. The editors of a new book are trying to save it.
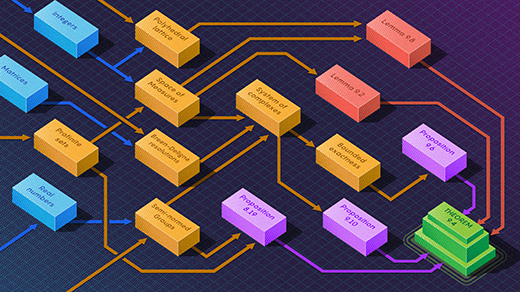
Proof Assistant Makes Jump to Big-League Math
Mathematicians using the computer program Lean have verified the accuracy of a difficult theorem at the cutting edge of research mathematics.
New Shape Opens ‘Wormhole’ Between Numbers and Geometry
Laurent Fargues and Peter Scholze have found a new, more powerful way of connecting number theory and geometry as part of the sweeping Langlands program.
A Video Tour of the Standard Model
The Standard Model is a sweeping equation that has correctly predicted the results of virtually every experiment ever conducted, as Quanta explores in a new video.
Nathan Seiberg on How Math Might Complete the Ultimate Physics Theory
Even in an incomplete state, quantum field theory is the most successful physical theory ever discovered. Nathan Seiberg, one of its leading architects, talks about the gaps in QFT and how mathematicians could fill them.
The Mystery at the Heart of Physics That Only Math Can Solve
The accelerating effort to understand the mathematics of quantum field theory will have profound consequences for both math and physics.
Mathematicians Answer Old Question About Odd Graphs
A pair of mathematicians solved a legendary question about the proportion of vertices in a graph with an odd number of connections.