Mathematical Simplicity May Drive Evolution’s Speed

When exploring a vast terrain of possible solutions to a problem, most paths are likely to be dead ends. But evolution may have found ways to improve the odds of success.
Ricardo Bessa for Quanta Magazine
Introduction
Creationists love to insist that evolution had to assemble upward of 300 amino acids in the right order to create just one medium-size human protein. With 20 possible amino acids to occupy each of those positions, there would seemingly have been more than 20300 possibilities to sift through, a quantity that renders the number of atoms in the observable universe inconsequential. Even if we discount redundancies that would make some of those sequences effectively equivalent, it would have been wildly improbable for evolution to have stumbled onto the correct combination through random mutations within even billions of years.
The fatal flaw in their argument is that evolution didn’t just test sequences randomly: The process of natural selection winnowed the field. Moreover, it seems likely that nature somehow also found other shortcuts, ways to narrow down the vast space of possibilities to smaller, explorable subsets more likely to yield useful solutions.
Computer scientists face similar challenges with problems that involve finding optimal solutions among astronomically huge sets of possibilities. Some have looked to biology for inspiration — even as biologists still try to figure out exactly how life does it, too.
Genetic algorithms, optimization methods that have been popular for decades, use the principles of natural selection to engineer new designs (for robots, drugs and transportation systems, among other things), train neural networks, or encrypt and decrypt data. The technique starts by treating random solutions to a problem as “organisms” that have certain features or elements “genetically” described in their code. These solutions aren’t particularly good, but they then undergo combinations of random mutations (and sometimes other changes that mimic gene-shuffling processes) to produce a second generation of organisms, which are in turn tested for their “fitness” at performing the desired task. Eventually, many repetitions of this process lead to a highly fit individual, or solution.
Some experts are taking the method a step further, in what’s known as genetic programming, to evolve software that could write programs and come up with solutions efficiently (the “genes” here might be programming instructions). This goal has proved particularly tricky, as researchers have had to take into account specific data types and structures, as well as other conditions.
Intriguingly, though, these evolution-based ways of thinking (genetic programming in particular) overlap conceptually with a mathematical theory that’s largely hovered on the sidelines of both biology and computer science. A handful of scientists have recently been trying to use it to gain insights into how evolution, both natural and artificial, can be efficient, generate novelty and learn to learn. The key: a specific notion of complexity, randomness and information that hasn’t had much practical application — until now.
Monkeys on Keyboards
That theory, developed in the 1960s, deals with what’s known as algorithmic information. It takes as its starting point an intuitive way of thinking about probability and complexity: the idea that, at least for some outputs, it’s computationally easier to describe how to generate something than to actually generate it. Take the well-worn analogy of a monkey pressing keys on a computer at random. The chances of it typing out the first 15,000 digits of pi are absurdly slim — and those chances decrease exponentially as the desired number of digits grows.
But if the monkey’s keystrokes are instead interpreted as randomly written computer programs for generating pi, the odds of success, or “algorithmic probability,” improve dramatically. A code for generating the first 15,000 digits of pi in the programming language C, for instance, can be as short as 133 characters.
In other words, algorithmic information theory essentially says that the probability of producing some types of outputs is far greater when randomness operates at the level of the program describing it rather than at the level of the output itself, because that program will be short. In this way, complex structures — fractals, for instance — can be more easily produced by chance.
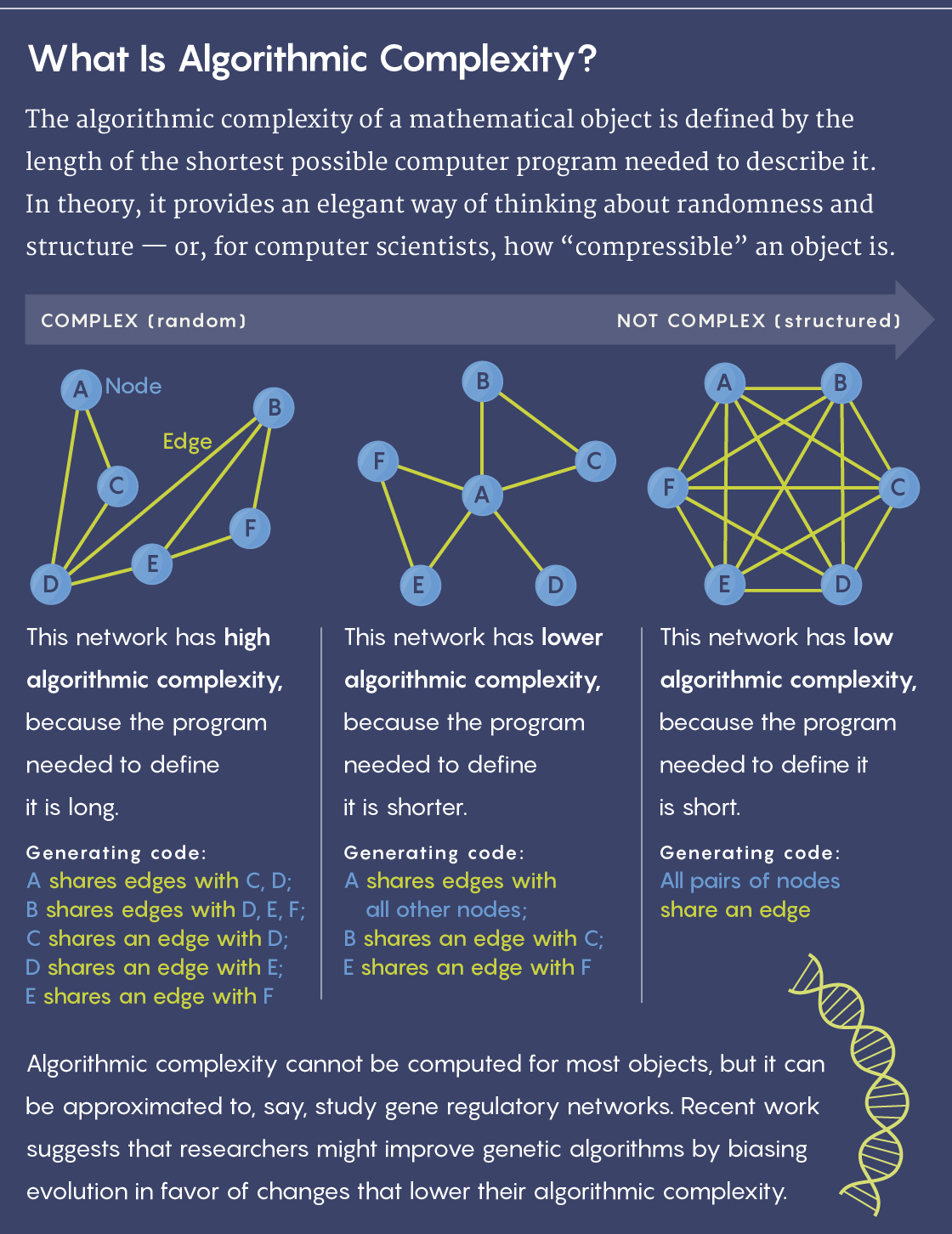
But a problem with that approach quickly emerged: Mathematicians learned that the algorithmic complexity (also known as Kolmogorov complexity, after Andrey Kolmogorov, one of the theory’s founders) of a given output — the length of the shortest possible program needed to specify it — is not computable. Computer scientists therefore couldn’t determine the ideal way to compress a string or other object.
Lucy Reading-Ikkanda/Quanta Magazine
As a result, algorithmic information theory was mostly relegated to the realm of pure mathematics, where it’s used for exploring related theorems and defining the concepts of randomness and structure. Practical uses seemed out of reach. “Mathematically, it’s a simple, beautiful measure of complexity,” said the noted mathematician Gregory Chaitin, formerly at the IBM Thomas J. Watson Center and the Federal University of Rio de Janeiro, and another of the theory’s founders. “But it looked unapproachable for real-world applications.”
That didn’t stop him from trying. He hoped the theory could be used to formalize the idea that DNA acts as software. In 2012, he published a book describing how evolution could be seen as a random walk through software space. The mutations along that walk, he argued, do not follow a statistically random probability distribution; instead, they follow a distribution based on Kolmogorov complexity. But he had no way to test it.
Now, some scientists are hoping to revive the theory in that context — to make it relevant to areas in both biology and computer science.
A Bias Toward Simplicity
Hector Zenil, a computer scientist at the Karolinska Institute in Sweden, is one of the people attempting to resurrect the theory. He’s been collaborating with other researchers to use Kolmogorov complexity as a metric for analyzing the complexity of biological networks, such as those that model gene regulation or protein interactions in cells. The researchers approximate the algorithmic information content of a network (since the actual value cannot be computed), then introduce a mutation to the network and test its effect on the Kolmogorov complexity. They hope that this method will reveal the relative importance of the network’s various elements, as well as how the network might respond functionally to intentional changes.

The noted mathematician Gregory Chaitin, one of the founders of algorithmic information theory, has argued that evolution can be understood as a kind of random computational walk through software space.
Courtesy of Gregory Chaitin
In one recent result posted on the preprint site arxiv.org, for instance, they found that moving the network toward greater Kolmogorov complexity — by introducing mutations that caused the network’s descriptive program to get longer — tended to increase the number of functions the system could perform while making it more sensitive to perturbation. If they nudged the network toward greater simplicity, fewer but more stable functions emerged.
But whether Kolmogorov complexity could act as something more than a tool — as the driving force of change that Chaitin believed it to be — remained to be seen. Despite its problems, algorithmic information does hold some appeal in the realm of biology. Traditionally, the mathematical framework used to describe evolutionary dynamics is population genetics — statistical models of how frequently genes may appear in a population. But population genetics has limitations: It can’t account for the origin of life and other major biological transitions, for instance, or for the emergence of entirely new genes. “A notion that sort of got lost in this lovely mathematical theory is the notion of biological creativity,” Chaitin said. But if we take algorithmic information into account, he said, “creativity fits in naturally.”
So does the idea that the evolutionary process itself is improving over time and becoming more efficient. “I’m quite convinced that evolution does intrinsically learn,” said Daniel Polani, a computer scientist and professor of artificial intelligence at the University of Hertfordshire in England. “And I would not be surprised if this would be expressible by algorithmic complexity going down asymptotically.”
Zenil and his team set out to explore experimentally the biological and computational implications of the algorithmic complexity framework. Using the same complexity approximation technique they had developed to analyze and perturb networks, they “evolved” artificial genetic networks toward certain targets — matrices of ones and zeros meant to represent interactions between genes — by biasing the mutations in favor of those that produced matrices with lower algorithmic complexity. In other words, they selected for greater structure.

Hector Zenil, a computer scientist at the Karolinska Institute in Sweden, seeks to analyze evolving biological networks in terms of their algorithmic (or Kolmogorov) complexity.
Courtesy of Hector Zenil, Photo by CSHV/Skof
They recently reported in Royal Society Open Science that, compared to statistically random mutations, this mutational bias caused the networks to evolve toward solutions significantly faster. Other features also emerged, including persistent, regular structures — sections within the matrices that had already achieved a degree of simplicity that new generations were unlikely to improve on. “Some regions were more prone or less prone to mutation, simply because they may have evolved some level of simplicity,” Zenil said. “This immediately looked like genes.” That genetic memory, in turn, yielded greater structure more quickly — implying, the researchers propose, that algorithmically probable mutations can lead to diversity explosions and extinctions, too.
“This means,” Zenil said, “that it’s fruitful to consider computational processes when we’re talking about evolution.” He hopes to use this understanding of randomness and complexity to identify pathways that may be more prone to mutation, or to figure out why certain genetic interactions might be associated with diseases like cancer.
Evolving Software
Zenil hopes to explore whether biological evolution operates according to the same computational rules, but most experts have their doubts. It’s unclear what natural mechanism could be responsible for approximating algorithmic complexity or putting that kind of mutational bias to work. Moreover, “thinking of life totally encoded in four letters is wrong,” said Giuseppe Longo, a mathematician at the National Center for Scientific Research in France. “DNA is extremely important, but it makes no sense if [it is] not in a cell, in an organism, in an ecosystem.” Other interactions are at play, and this application of algorithmic information cannot capture the extent of that complexity.
Still, the concept has piqued some interest — particularly since this way of thinking about evolution and computational processes seems to have something in common, at least thematically, with genetic programming’s aim of evolving software.
Indeed, there have been some intriguing hints at a potential link between Chaitin and Zenil’s ideas about Kolmogorov complexity and genetic programming methods. In 2001, for instance, a team of researchers reported that the complexity of the output of a genetic program can be bounded by the Kolmogorov complexity of the original program.
But for the most part, Kolmogorov complexity has not played a role in computer scientists’ understanding of those ideas. Instead, they’ve tried other ways of modifying the genetics and mutations involved. Some groups have skewed the rates of mutations; others have biased the system to favor mutations that replace larger chunks of code. “There are dozens, maybe hundreds, of different versions of mutations and crossover that people have come up with,” said Lee Spector, a computer scientist at Hampshire College in Massachusetts. Spector recently led a team that showed the advantages of adding and deleting mutations throughout their organisms’ genomes, instead of always directly replacing one gene with another. This new kind of genetic operator ended up exponentially expanding the number of paths through the genomic search space and led to better solutions.

Lee Spector, a computer scientist at Hampshire College, hopes to greatly improve the potential of artificial intelligence by developing new genetic programming techniques.
Courtesy of Lee Spector
That said, many researchers have gone in the opposite direction, hunting for clever ways to speed up the process by narrowing the search space, without limiting it so much that the search misses optimal results. One idea has been to make simplicity a target: Just as Eugene Wigner noted the “unreasonable effectiveness of mathematics in the natural sciences” in 1960, computer scientists have found that simpler, more elegant models often prove to be more generally applicable and effective. “And the question is,” Spector said, “is it telling us something deep about the universe, or not? And in any event, does it seem to be useful?”
He also warns that attempts to bias evolving programs toward simplicity can be destructive, too: Rewarding something like shorter program lengths, for example, could trim putative junk that might have been helpful in later generations, sacrificing what could have been optimal solutions in the process. “So you get stuck,” he said.
But simplicity remains a tantalizing goal, and one that’s also proved useful. In work published last year, Spector and his colleagues found that if they reduced the size of their programs —sometimes to as little as 25 percent of their original size — after they performed their genetic programming techniques, the programs performed better on new data and could be used for a wider range of general problems.
That’s in part why he’s been keeping his eye on work being done in algorithmic information theory, though he says he has yet to see exactly how it will influence the field.
Learning From Life
Perhaps Zenil’s team has taken a first step toward finding that influence — but to make their work’s applications more generally realistic, they will first have to test their method on other types of search problems.
Still, “they have a very good point in restricting based on structure,” said Larissa Albantakis, a theoretical neuroscientist at the University of Wisconsin, Madison, who has also done work on speeding up genetic algorithms by limiting the search space they have to traverse. “Nature is structured, in many ways, and if you take that as your starting point, then it’s kind of silly to try all possible uniform mutations.”
She added, “Anything meaningful to us is structured in some way or another.”
While Spector remains skeptical that Zenil’s recent work has applications beyond the very specific problem he explored, “the information theory behind the concepts here is intriguing and potentially quite important,” he said. “I find it exciting in part because it seems to be on another planet. Maybe there are insights that folks in our community aren’t aware of.” Algorithmic information, after all, taps into a wide array of notions that some experts in genetic programming may not incorporate into their work, including the open-ended nature of evolution.
“I have a strong sense that there’s important stuff here,” Spector said. Even so, he added, right now “there’s still a huge distance between what they’re working on and practical applications.”
“The idea of thinking about life as evolving software is fertile,” Chaitin said, though it may be premature to judge its worth. Whether thinking about artificial or biological life, “we need to see how far we’ll get.”





