Scientists Conjure Curves From Flatness

Try gift-wrapping a soccer ball, and you will quickly encounter the geometric abyss between paper’s inherent flatness and a sphere’s natural curves.

“The very first bit seems to sort of match, but as you wrap the paper around, the crinkles get bigger and bigger,” observed Toen Castle, a physicist at the University of Pennsylvania.

With their concave curves, saddles are equally tough to wrap, but for the opposite reason. “There’s more saddle than there is paper,” Castle said.

The mismatch between soccer balls, saddles and sheets of paper lies in their “intrinsic” curvature, a property of surfaces known to mathematicians for centuries that no amount of folding can change. Scientists have sought a bridge across the divide — a systematic way of imbuing flat surfaces with curvature, which they say could revolutionize the design and assembly of three-dimensional structures and help extend a major theorem of geometry.

Now, Castle and several Penn colleagues have found just such a bridge in the same technique that tailors use to hug fabric around the curves of a body — namely, by making the right cuts. Reporting their work in December in Physical Review Letters, the physicists present a basic set of rules for cutting and reconnecting a piece of paper in order to add curvature to one point in its surface while subtracting it from another, maintaining the paper’s overall flatness while forcing it to bend into the third dimension.

“It’s a way of encoding three-dimensionality in a two-dimensional structure,” said Randall Kamien, a professor of physics at Penn who heads the research group behind the result. “The whole thing will just pop up all by itself.”

The new work essentially provides a rule book for a restricted version of kirigami, a less famous cousin of origami, the ancient Japanese art of paper folding. Origami approximates curved surfaces through folding, which changes paper’s “extrinsic” curvature in space. But through a combination of folds and cuts, kirigami artists produce Escheresque stairways, domed cathedrals and undulating water waves by embedding curvature directly into paper. Kamien and his team have shown that even their restricted kirigami, in which cuts and folds must preserve the spacing of a honeycomb lattice on the paper’s surface, allows the construction of a virtually unlimited range of 3-D structures.

“It’s a concrete and elegant step forward,” said Vincenzo Vitelli, a physicist at Leiden University in the Netherlands.

To picture intrinsic curvature, draw a triangle on a sheet of paper. Its interior angles add up to 180 degrees even after you roll the sheet into a cylinder or fold it into an origami crane. The 180-degree total signifies flatness, according to a 19th-century formula called the Gauss-Bonnet theorem that relates the intrinsic curvature of a surface to the interior angles of a closed path around it. The angles of a triangle exceed 180 degrees on the bulging, “positively curved” surface of a sphere and pinch inward, falling short of that total, on a “negatively curved” saddle.

Lattice Kirigami: The Four Rules

Kirigami artists cut and fold a single sheet of paper into elaborate 3-D structures. Now, scientists at the University of Pennsylvania have discovered a set of four rules that govern a restricted version of kirigami called “hexagonal lattice kirigami,” in which cuts and folds must preserve the spacing of a honeycomb lattice on the paper’s surface. Starting with a printout of a honeycomb lattice (pdf), you can follow these rules to build a limitless variety of structures.

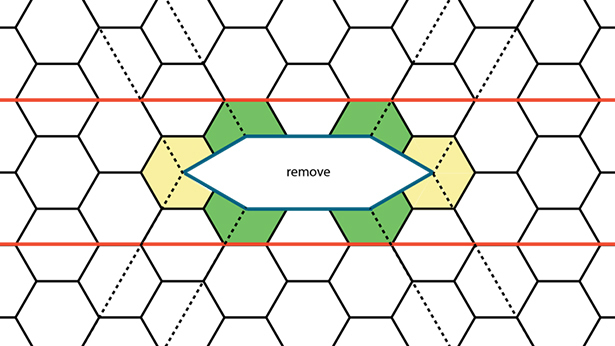
1. The basic building blocks of hexagonal lattice kirigami are step-like structures called the “5-7 pair” and “2-4 pair.” To create a 5-7 pair, first cut out an equilateral triangle connecting the centers of three mutually adjacent hexagons. To create a 2-4 pair, cut out an isosceles triangle whose two equal edges are adjacent edges of a hexagon.

2. Each 5-7 (or 2-4) pair must connect with another pair using “glide” and “climb” cuts. In a pure glide, a single cut extends in a straight line through an edge of both excised triangles (see this glide template). In a pure climb, parallel cuts connect two corners of the triangles (see this climb template). Pairs can also connect through a mix of climb and glide components.

3. The paper must be folded along lines perpendicular to the cut edges in order to form plateaus with vertical walls.

4. Because 2-4 pairs and 5-7 pairs produce vertical walls of different heights, plateaus must be created by pairs of the same type.

For decades, mathematicians have studied how nature deals with the resulting soccer-ball-wrapping problem, or the challenge of bending 2-D lattices of seeds, leaves or cells around curves. French researchers showed in 2012 that the honeycomb lattice of seeds covering the dome of a sunflower contains a precise pattern of structural “defects” that allows it to rise over the dome. Most seeds in the lattice have six neighbors, but each defect consists of a pentagonal arrangement of seeds near a heptagonal arrangement, in place of two hexagons.

“The seeds make this beautiful spiral pattern,” Kamien said.

Inspired by the work on sunflowers, the Penn scientists treated their kirigami paper much like a hexagonal lattice of seeds. Over the course of hundreds of hours of cutting and folding, they discovered the rules for removing wedges from paper and gluing the holes closed to convert two hexagons into a pentagon and a heptagon, or a “5-7 pair.” They also found construction rules for a “dual” or geometrically related defect called a 2-4 pair, which converts the number of edges that meet at the corners of neighboring hexagons from three to two and four.

To understand how these defects lift a flat surface into the third dimension, imagine a bug crawling on a sheet of paper. Initially, the bug makes six 60-degree turns for a total angular rotation of 360 degrees to return to its starting point, tracing out the shape of a hexagon. According to the Gauss-Bonnet theorem, this signifies zero curvature. But if the scientists remove a triangular wedge from the hexagon according to their rule book and glue the cut edges together, the paper no longer lies flat. The bug must make only five 60-degree turns to get back where it started, a deficit that indicates that this pentagonal patch of the surface now has positive curvature. Nearby, the bug must make seven such turns, signifying a heptagon with an equal and opposite amount of negative curvature, the kind in a saddle. Even as the paper’s overall curvature remains zero, the 5-7 pair steps it up to a new plane.

The new work gives scientists, engineers and mathematicians a handle on how to convert sixes into fives and sevens, explained Christian Santangelo, a physicist at the University of Massachusetts, Amherst. “The Gauss-Bonnet theorem doesn’t tell you what cuts and folds you need to set up the intrinsic curvature, how far the folds extend, how they interfere with each other,” he said. “That’s the gap these guys have closed.”

The rule book turns kirigami into a new and efficient approach for designing 3-D structures, researchers said. Whereas building objects with origami requires intricate folding, construction in kirigami is simply a matter of closing the holes that have been pre-cut in paper or any other flat material. “Just by printing holes onto something, you control how you pop it up,” Santangelo said.

The scientists hope the work will translate into an algorithm for designing target structures at any scale, from nano-devices built from graphene sheets to shape-shifting robots and self-assembling shelters. “I could send you something through the mail, folded flat, and you could open it and it pops up into a tent,” said Daniel Sussman, a postdoctoral researcher at Penn and a co-author of the new paper.

But the kirigami rules do not explain how 5-7 defects are created and used to greatest effect in nature. Nicolas Rivier of Louis Pasteur University in Strasbourg, one of the three French mathematicians who modeled the geometry of sunflower domes, said it isn’t known whether the pattern of 5-7 pairs in many biological systems is the result of evolution or pure mechanics.

“The funny thing is that the plant does it automatically,” Rivier said. “You cannot cut the plant.”

[email protected](Email us) a photo of your kirigami creations. (Make sure to include the word “kirigami” in the subject line.) We’ll post our favorite submissions to Quanta’s Facebook page.

Editor’s Note: Randall Kamien receives funding from the Simons Foundation as a Simons Investigator.

This article was reprinted on Wired.com.