Solution: ‘Sleeping Beauty’s Dilemma’

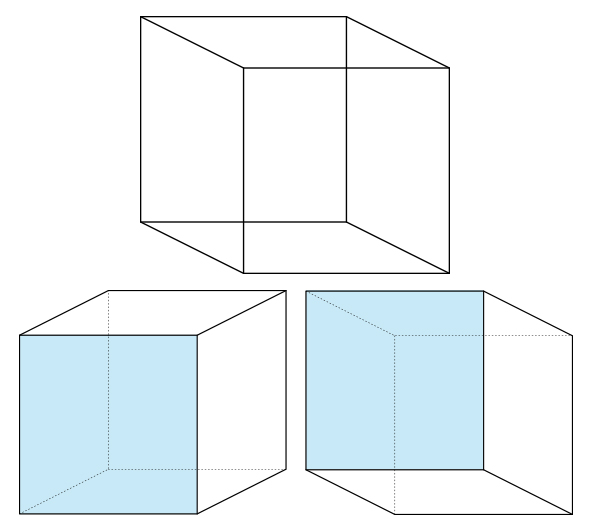
This month’s puzzle featured two variations on the famous Sleeping Beauty problem. We compared the original problem to a famous visual illusion, the Necker cube, which is a two-dimensional figure that can be perceived as a three-dimensional object in one of two different orientations, with both perceptions equally valid. The Sleeping Beauty problem has spawned two clear-cut camps known as the halfers and the thirders. There are dozens, perhaps hundreds of papers offering highly sophisticated arguments supporting one side or the other. It is astonishing and a little unsettling to some that such a situation can arise in a branch of mathematics, in this case probability or decision theory. Are there ambiguities at the core of these disciplines that can undermine them? Certainly not in this instance: The underlying specific procedures here are very well-defined and do yield answers that everyone can agree on when problems are specific enough. Yet there is plenty to argue about in the Sleeping Beauty problem, so let’s dive into the original scenario.

The famous fairy-tale princess Sleeping Beauty participates in an experiment that starts on Sunday. She is told that she will be put to sleep, and while she is asleep a fair coin will be tossed that will determine how the experiment will proceed. If the coin comes up heads, she will be awakened on Monday, interviewed, and put back to sleep, but she won’t remember this awakening. If the coin comes up tails, she will be awakened and interviewed on Monday and Tuesday, again without remembering either awakening. In either case, the experiment ends when she is awakened on Wednesday without being interviewed.

Whenever Sleeping Beauty is awakened and interviewed, she won’t know which day it is or whether she has been awakened before. During each awakening, she is asked: “What is your degree of certainty* that the coin landed heads?” What should her answer be?

*(This is sometimes worded as “credence,” “degree of belief,” “subjective probability” or “subjective certainty.”)

As I discussed when I presented the puzzle, the halfers, whose position was first articulated by David Lewis in 2001, assert that the answer is one-half. Since the coin was fair, the chance that it came up heads is half. Sleeping Beauty receives no new information about the result of the coin toss when she is awakened. So her subjective probability that the coin came up heads should continue to be one-half.

Thirders, following and extending Adam Elga’s argument in 2000, argue that there are three possible situations in which Sleeping Beauty could have been awakened, which are indistinguishable to her. The coin could have come up heads and it is Monday, the coin could have come up tails and it is Monday, or the coin could have come up tails and it is Tuesday. Each of these is equally likely from her perspective, so the probability of each is one-third. Since the coin comes up heads in only one of these situations, her subjective probability that the coin came up heads is one-third.

One reason for the differences between the two camps is that halfers and thirders interpret the question in two different, though equally valid, ways, and translate it into slightly different mathematical problems. Credence is an intermediate mental construct that is defined differently by the two camps. As Quanta reader Josh put it, “Like most verbal paradoxes, [this dilemma] relies on underspecifying the precise question!” When the question is put in precise mathematical terms, there is no paradox, and both halfers and thirders get the same answer — just as the ambiguity of the Necker cube is resolved if the front face is specified, as in the accompanying illustration. There can be clear-cut answers, then, as we shall see in our well-specified variations — there’s no need to worry about the foundations of probability. It’s just a matter of being specific about what is asked, as we saw in an earlier Insights column.

And yet, in its original form, this problem has generated a huge philosophical and psychological chasm between the two positions, in a way that the Necker cube has not, since most people can flip quite easily from one percept to the other. Each Sleeping Beauty camp is passionate about its stance. I know from personal experience that arguments with someone in the opposite camp are usually futile. It’s far more productive to try and nail down the differences in thought between the two camps and get at least an intellectual, if not intuitive, appreciation of the opposing camp’s mindset. I have attempted to depict the differences in the thought processes experienced by the two camps in the chart below.

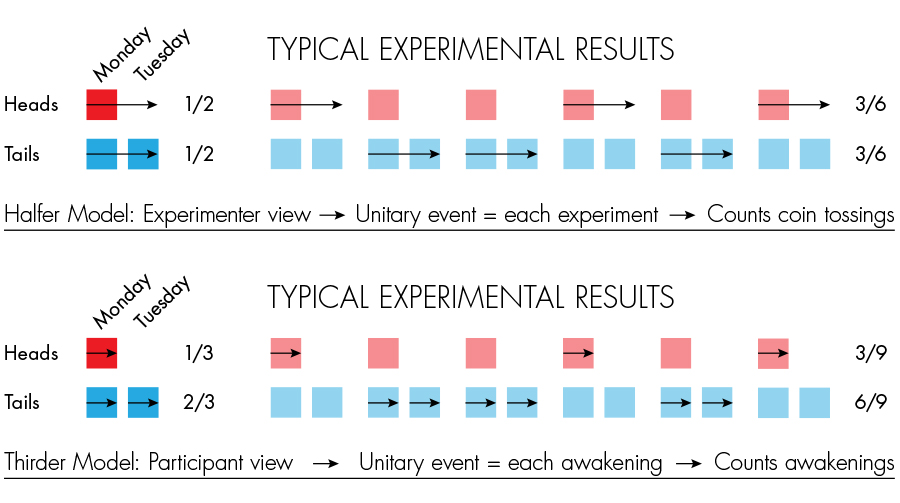Halfers take an experimenter’s view: For them, the question is about which of the two arms of the study Sleeping Beauty is in — the heads (red) or the tails (blue) arm as depicted in the top part of the figure. Each of the arrows shown in the figure represents a completed “trial.” The detailed setup of the experiment — the amnesia, and the number of awakenings — is irrelevant, “a snare and a delusion” in the words of halfer Peter Winkler. In this view, Sleeping Beauty has no specific information as to whether the coin landed tails or heads because she is awakened per the original protocol regardless of what happens. So if the experiment were repeated many times, halfers would count the number of times she ended up in the heads arm of the experiment, relative to the total number of trials. Since it is given that the coin is fair, this will happen in one-half of the trials.

Thirders focus on the subject’s view: For them, the question has to do with which timeline she is more likely to be in when she is awakened, that of a heads or a tails toss. She is twice as likely to be in the tails timeline when she is awakened as she is to be in the heads timeline, as seen in the fact that there are twice as many arrows on the blue waking panels as there are on the red ones. The detailed setup of the experiment such as the amnesia and the difference in the number of awakenings in the two coin states — whether one, two, or a million — is now of vital importance and will drastically change the degree of belief the subject has about which coin-toss timeline she was awakened in. To a thirder, the information that Sleeping Beauty receives is contained in a combination of three things: 1) The details of the experiment protocol known to her beforehand, which in this case samples the two tosses differently, 2) the amnesia which makes all the awakenings identical from her point of view, and, crucially, 3) the realization that “I am now awake.” So if the experiment were repeated many times, thirders would count the number of awakenings that happen in the heads timeline relative to the total number of awakenings. Since there is only one awakening for a heads toss out of every three awakenings, the subjective probability of the coin toss having come up heads will be one-third.

To dig a little deeper into the halfer-thirder quarrel, at its heart it’s a disagreement about what constitutes valid information that Sleeping Beauty can use to update her probability about what happened in the coin toss. This is an extremely subtle point. Interested readers can check out a modified experiment I set forth in a comment dated January 27, 2016, which describes the kind of information that both parties agree compels Sleeping Beauty to update her probability for the coin toss per textbook Bayesian criteria. But this consensus fails in the case of the original Sleeping Beauty problem. I’ve come to believe that the gap cannot be bridged, and that the difference in approach perhaps arises from some deep intuitive source, such as gut-level responses arising from early training or kinds of mathematical problems encountered or even psychological or personality traits. This is not an unprecedented situation. The basis for another seemingly irreconcilable polarization — between liberals and conservatives — has been traced by the psychologist Jonathan Haidt to deep gut-level intuitions arising from emotional and personality differences. Are halfers better at visualizing points of view outside themselves? Do thirders tend to be temperamentally pragmatic? It might make for an interesting psychological research project.

OK, so we’ve seen that halfers and thirders completely disagree about nebulous things like credences and subjective probabilities. But here’s the key point: When challenged with a well-specified problem with clearly stated utility functions (probabilities of specific payoffs) linked to each alternative, skilled halfers and thirders have no difficulty in selecting the proper model to apply (even if it’s not their default one), applying the laws of probability correctly and getting the right answer! The proof of the pudding in probability problems is in the making of a concrete bet that has one answer that gives the best result, as in the two variations presented in this month’s puzzle. The halfers and thirders all got the correct answer, even though it was not their default stance. As a mathematics teacher or puzzle columnist would say, “Go figure!” On a more serious note, this shows that the laws of probability are indeed rock-solid, and the two dueling positions are only based on default gut-level points of view that do not get in the way of finding the right answer to a well-specified problem.

The two concrete variations we presented were based on a scenario created by Quanta reader eJ. They were as follows:

Variation 1:

Upon each awakening, Sleeping Beauty is presented with two bags of beans, marked “H” and “T.” She is instructed to reach into one bag, grab a single bean, and put it aside. At the end of the experiment, she will have to eat the bean or beans that she has pulled. She is told that the bags are filled with identical looking jellybeans (J) or poisoned pills (K), as follows:

• If the coin came up heads, bag H has 7J, and bag T has 7K.
• If the coin came up tails, bag H has 1J and 6K, while bag T has 6J and 1K.

You are Sleeping Beauty. Which bag would you pick, and what are your chances of survival?

Variation 2:

You, as Sleeping Beauty, are told that you have to go through the original experiment (without the beans) every week for many months, and the memory of each waking will be wiped from your memory. The evil chief scientist has determined that on your hundredth awakening in this series of experiments, you will be presented with the two bags of beans and instructed exactly as in Variation 1 above. If you pick a poisoned pill, you will die; otherwise, you will go free. Now which bag do you pick, and what are your chances of surviving?

In these two problems, you are given the same utility function, so the calculations are very similar. For each variation, you multiply the likelihood of the desired outcome by your probability estimate for the appropriate coin toss for every possible alternative and add all the cases to get your final likelihood of survival. Let’s check out how the halfer and the thirder would fare in the two problems. Remember, probability calculations boil down to nothing more than counting carefully. We discuss Variation 1 in detail here, and leave Variation 2 to the reader. The qualitative results for the two are identical.

If you are a halfer and you pick bag H:

• If the coin landed heads (your estimated probability: 1/2) you will definitely pick a J (1), giving 1/2 x 1 = 1/2.
• If the coin landed tails (p = 1/2), you will need to be lucky enough to pick the jellybean out of the H bag on both Monday and Tuesday to survive, so your chances are (1/7 x 1/7) x 1/2, giving 1/98.

Adding the two probabilities makes your overall chance of survival 1/2 + 1/98 = 25/49 (51 percent).

If you are a halfer and you pick bag T:

• If the coin landed heads (p = 1/2) you cannot pick a J (0), giving 1/2 x 0 = 0.
• If the coin landed tails (p = 1/2), you need to pick a J out of the T bag on both Monday and Tuesday to survive, so your chances are (6/7 x 6/7) x 1/2, giving 18/49.

Adding the two probabilities makes your overall chance of survival 0 + 18/49 = 18/49 (37 percent).

So if you are an inflexible halfer, you will pick bag H for both problems.

If you are a thirder and you pick bag H:

• If the coin landed heads (your estimate: p = 1/3) you will definitely pick a J (1), giving 1/3 x 1 = 1/3.
• If the coin landed tails (p = 2/3), you need to pick the J out of the H bag on both Monday and Tuesday to survive, so your chances are (1/7 x 1/7) x 2/3, giving 2/147.

Adding the two probabilities makes your overall chance of survival 1/3 + 2/147 = 51/147 (35 percent).

If you are a thirder and you pick bag T:

• If the coin landed heads (p = 1/3) you cannot pick a J (0), giving 1/3 x 0 = 0
• If the coin landed tails (p = 2/3), you need to pick a J out of the T bag on both Monday and Tuesday to survive, so your chances are (6/7 x 6/7) x 2/3, giving 24/49.

Adding the two probabilities makes your overall chances of survival 0 + 24/49 = 24/49 (49 percent).

If you are an inflexible thirder, you will pick bag T for both problems.

Note the beauty of eJ’s scenario: Your choice of bag, H or T, perfectly reflects whether you are acting as a halfer or a thirder.

But wait, who is correct? We saw above that halfers and thirders model different problems. Which categories do these two variations belong to?

In Variation 1, your fate is decided after you have gone through one arm of the experiment or the other as in the top part of the diagram. This requires the kind of counting that is correctly modeled by a halfer. So that’s what you need to be. The correct bag to pick is H.

In Variation 2, your fate is based on a single selected awakening, picked, for all practical purposes, at random. This requires the kind of counting that is correctly modeled by a thirder, and so the correct bag to pick is T.

Our readers, whether they identified as halfers or thirders, picked the correct answers in both cases. So there you have it. Halfers are halfers, and thirders are thirders, and never the twain shall meet — unless they are solving a concrete problem and getting the same result! Here’s a quantum analogy: The Sleeping Beauty problem is like an unobservable particle in a quantum superposition of 50 percent H and 50 percent T among the ensemble of puzzle enthusiasts. As in quantum mechanics, when an actual measurement is made (a concrete question is posed), the state is correctly found by the ensemble to be either H or T.

I thank all readers for providing great insights, ideas and references. I’d especially like to thank Joel Pust for providing a link to the extensive philosophical literature, and Josh for citing and summarizing Berry Groisman’s paper declaring everyone to be winners. In awarding the Quanta T-shirt this week, I’d like to endorse the suggestion expressed to me by eJ: “The T-shirt winner needs to demonstrate some respect for both sides of the argument.” The T-shirt therefore goes to Josh, narrowly beating out the similarly excellent contributions of Paul Smaldino, Robert and Dan. I think everyone will agree that eJ deserves a T-shirt too, for proposing these two ingenious variations. Congratulations!