A Bird’s-Eye View of Nature’s Hidden Order
Olena Shmahalo/Quanta Magazine; Photography: MTSOfan and Matthew Toomey
Introduction
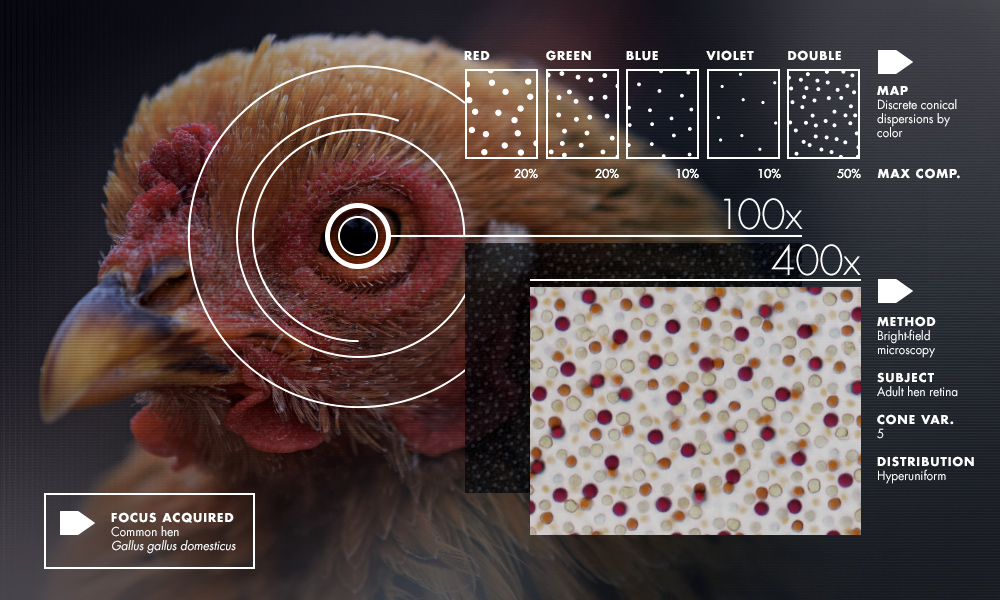
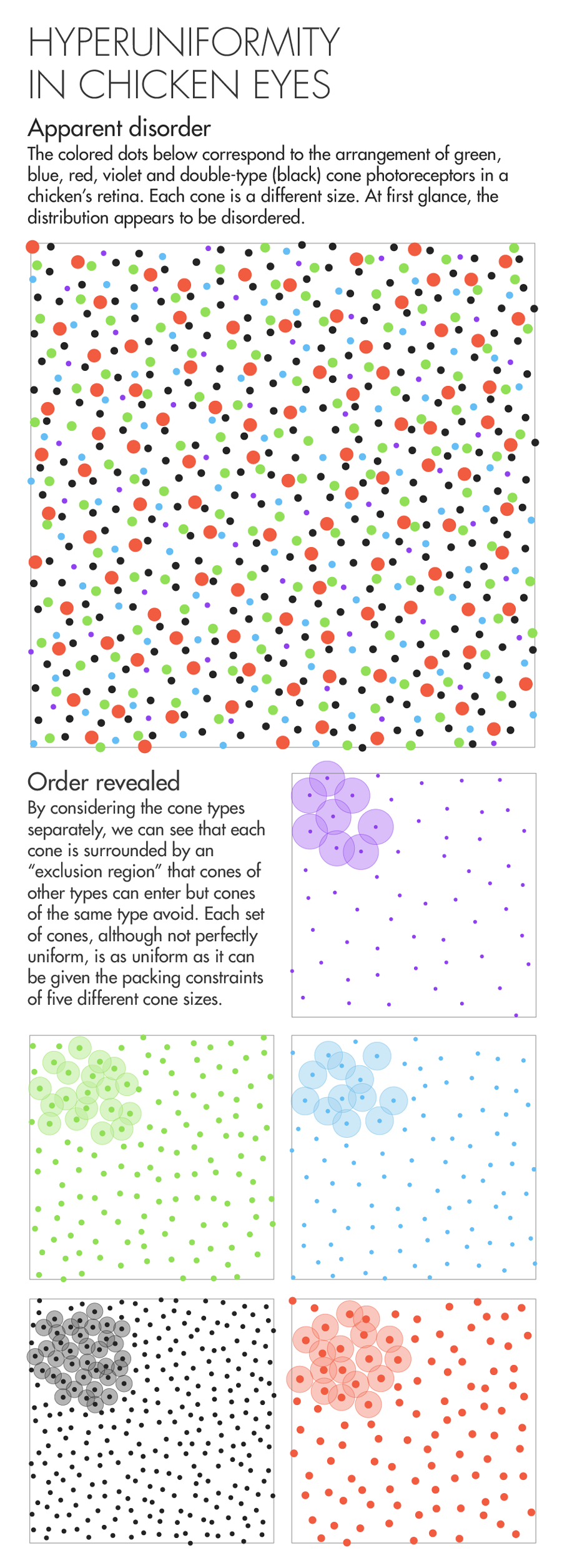
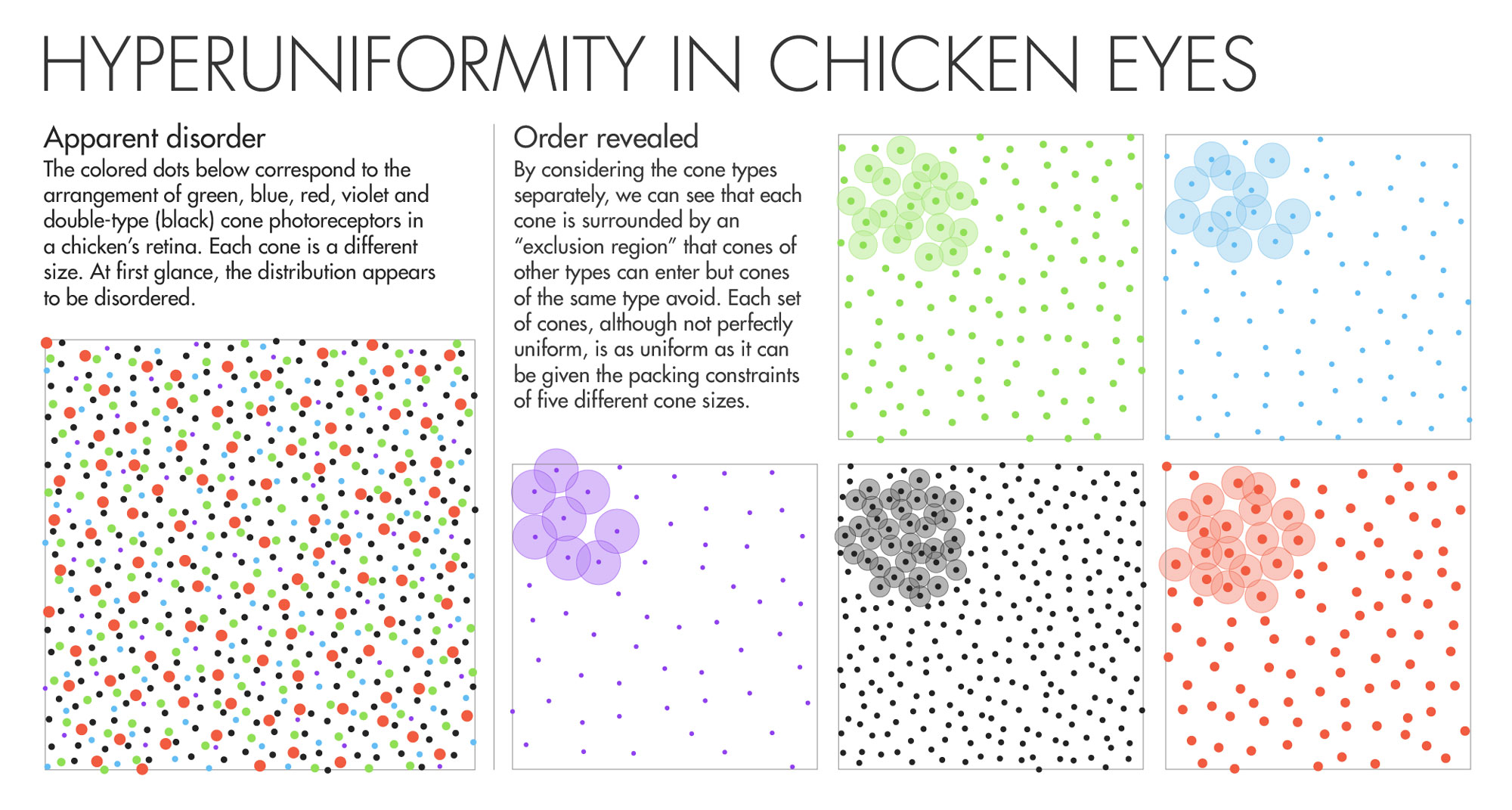
Seven years ago, Joe Corbo stared into the eye of a chicken and saw something astonishing. The color-sensitive cone cells that carpeted the retina (detached from the fowl, and mounted under a microscope) appeared as polka dots of five different colors and sizes. But Corbo observed that, unlike the randomly dispersed cones in human eyes, or the neat rows of cones in the eyes of many fish, the chicken’s cones had a haphazard and yet remarkably uniform distribution. The dots’ locations followed no discernible rule, and yet dots never appeared too close together or too far apart. Each of the five interspersed sets of cones, and all of them together, exhibited this same arresting mix of randomness and regularity. Corbo, who runs a biology lab at Washington University in St. Louis, was hooked.
“It’s extremely beautiful just to look at these patterns,” he said. “We were kind of captured by the beauty, and had, purely out of curiosity, the desire to understand the patterns better.” He and his collaborators also hoped to figure out the patterns’ function, and how they were generated. He didn’t know then that these same questions were being asked in numerous other contexts, or that he had found the first biological manifestation of a type of hidden order that has also turned up all over mathematics and physics.
Corbo did know that whatever bird retinas are doing is probably the thing to do. Avian vision works spectacularly well (enabling eagles, for instance, to spot mice from a mile high), and his lab studies the evolutionary adaptations that make this so. Many of these attributes are believed to have been passed down to birds from a lizardlike creature that, 300 million years ago, gave rise to both dinosaurs and proto-mammals. While birds’ ancestors, the dinos, ruled the planetary roost, our mammalian kin scurried around in the dark, fearfully nocturnal and gradually losing color discrimination. Mammals’ cone types dropped to two — a nadir from which we are still clambering back. About 30 million years ago, one of our primate ancestors’ cones split into two — red- and green-detecting — which, together with the existing blue-detecting cone, give us trichromatic vision. But our cones, particularly the newer red and green ones, have a clumpy, scattershot distribution and sample light unevenly.
Bird eyes have had eons longer to optimize. Along with their higher cone count, they achieve a far more regular spacing of the cells. But why, Corbo and colleagues wondered, had evolution not opted for the perfect regularity of a grid or “lattice” distribution of cones? The strange, uncategorizable pattern they observed in the retinas was, in all likelihood, optimizing some unknown set of constraints. What these were, what the pattern was, and how the avian visual system achieved it remained unclear. The biologists did their best to quantify the regularity in the retinas, but this was unfamiliar terrain, and they needed help. In 2012, Corbo contacted Salvatore Torquato, a professor of theoretical chemistry at Princeton University and a renowned expert in a discipline known as “packing.” Packing problems ask about the densest way to pack objects (such as cone cells of five different sizes) in a given number of dimensions (in the case of a retina, two). “I wanted to get at this question of whether such a system was optimally packed,” Corbo said. Intrigued, Torquato ran some algorithms on digital images of the retinal patterns and “was astounded,” Corbo recalled, “to see the same phenomenon occurring in these systems as they’d seen in a lot of inorganic or physical systems.”
Lucy Reading-Ikkanda for Quanta Magazine
Torquato had been studying this hidden order since the early 2000s, when he dubbed it “hyperuniformity.” (This term has largely won out over “superhomogeneity,” coined around the same time by Joel Lebowitz of Rutgers University.) Since then, it has turned up in a rapidly expanding family of systems. Beyond bird eyes, hyperuniformity is found in materials called quasicrystals, as well as in mathematical matrices full of random numbers, the large-scale structure of the universe, quantum ensembles, and soft-matter systems like emulsions and colloids.
Scientists are nearly always taken by surprise when it pops up in new places, as if playing whack-a-mole with the universe. They are still searching for a unifying concept underlying these occurrences. In the process, they’ve uncovered novel properties of hyperuniform materials that could prove technologically useful.
From a mathematical standpoint, “the more you study it, the more elegant and conceptually compelling it seems,” said Henry Cohn, a mathematician and packing expert at Microsoft Research New England, referring to hyperuniformity. “On the other hand, what surprises me about it is the potential breadth of its applications.”
A Secret Order
Torquato and a colleague launched the study of hyperuniformity 13 years ago, describing it theoretically and identifying a simple yet surprising example: “You take marbles, you put them in a container, you shake them up until they jam,” Torquato said in his Princeton office this spring. “That system is hyperuniform.”
The marbles fall into an arrangement, technically called the “maximally random jammed packing,” in which they fill 64 percent of space. (The rest is empty air.) This is less than in the densest possible arrangement of spheres — the lattice packing used to stack oranges in a crate, which fills 74 percent of space. But lattice packings aren’t always possible to achieve. You can’t easily shake a boxful of marbles into a crystalline arrangement. Neither can you form a lattice, Torquato explained, by arranging objects of five different sizes, such as the cones in chicken eyes.
As stand-ins for cones, consider coins on a tabletop. “If you take pennies, and you try to compress the pennies, the pennies like to go into the triangular lattice,” Torquato said. But throw some nickels in with the pennies, and “that stops it from crystallizing. Now if you have five different components — throw in quarters, throw in dimes, whatever — that inhibits crystallization even further.” Likewise, geometry demands that avian cone cells be disordered. But there’s a competing evolutionary demand for the retina to sample light as uniformly as possible, with blue cones positioned far from other blue cones, reds far from other reds, and so on. Balancing these constraints, the system “settles for disordered hyperuniformity,” Torquato said.
Hyperuniformity gives birds the best of both worlds: Five cone types, arranged in near-uniform mosaics, provide phenomenal color resolution. But it’s a “hidden order that you really can’t detect with your eye,” he said.
Determining whether a system is hyperuniform requires algorithms that work rather like a game of ring toss. First, Torquato said, imagine repeatedly tossing a ring onto an orderly lattice of dots, and each time it lands, counting the number of dots inside the ring. The number of captured dots fluctuates from one ring toss to the next — but not by very much. That’s because the interior of the ring always covers a fixed block of dots; the only variation in the number of captured dots happens along the ring’s perimeter. If you increase the size of the ring, you will get variation along a longer perimeter. And so with a lattice, the variation in the number of captured dots (or “density fluctuations” in the lattice) grows in proportion to the length of the ring’s perimeter. (In higher spatial dimensions, the density fluctuations also scale in proportion to the number of dimensions minus one.)
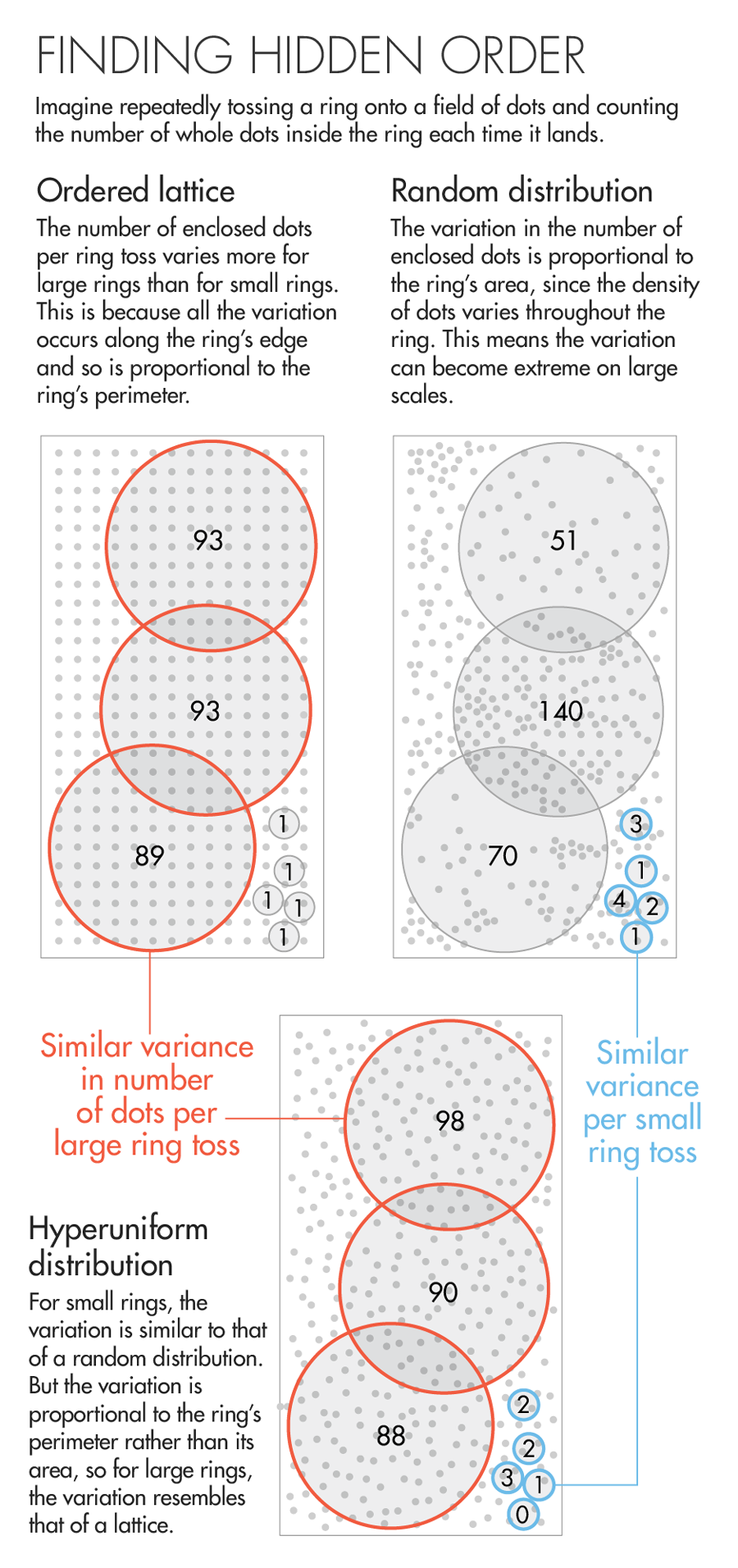
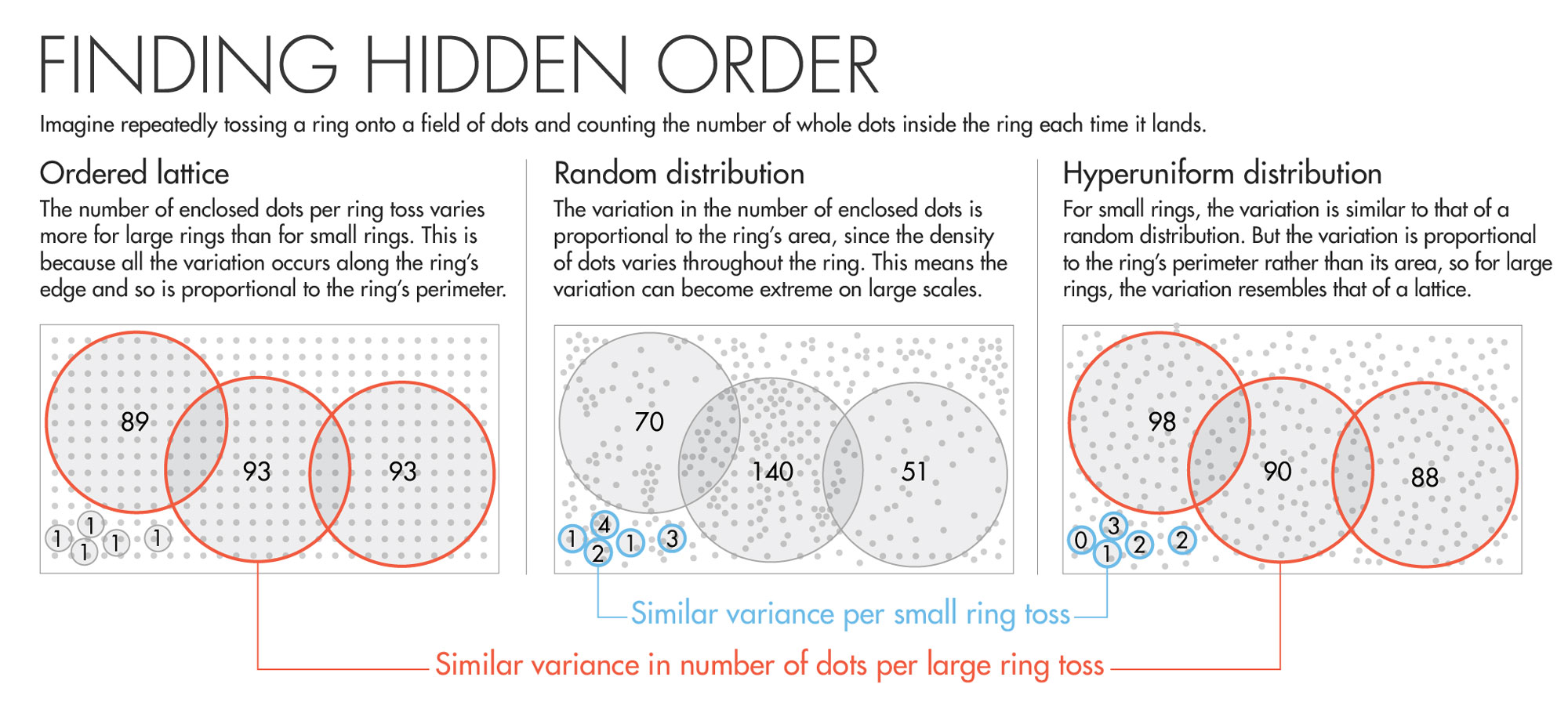
Lucy Reading-Ikkanda for Quanta Magazine
Now imagine playing ring toss with a smattering of uncorrelated dots — a random distribution, marked by gaps and clusters. A hallmark of randomness is that, as you make the ring bigger, the variation in the number of captured dots scales in proportion to the ring’s area, rather than its perimeter. The result is that on large scales, the density fluctuations between ring tosses in a random distribution are much more extreme than in a lattice.
The game gets interesting when it involves hyperuniform distributions. The dots are locally disordered, so for small ring sizes, the number of captured dots fluctuates from one toss to the next more than in a lattice. But as you make the ring bigger, the density fluctuations begin to grow in proportion to the ring’s perimeter, rather than its area. This means that the large-scale density of the distribution is just as uniform as that of a lattice.
Among hyperuniform systems, researchers have found a further “zoology of structures,” said the Princeton physicist Paul Steinhardt. In these systems, the growth of density fluctuations depends on different powers (between one and two) of the ring’s perimeter, multiplied by different coefficients.
“What does it all mean?” Torquato said. “We don’t know. It’s evolving. There are a lot of papers coming out.”
Material Menagerie
Hyperuniformity is clearly a state to which diverse systems converge, but the explanation for its universality is a work in progress. “I see hyperuniformity as basically a hallmark of deeper optimization processes of some sort,” Cohn said. But what these processes are “might vary a lot between different problems.”
Hyperuniform systems fall into two main classes. Those in the first class, such as quasicrystals — bizarre solids whose interlocked atoms follow no repeating pattern, yet tessellate space — appear to be hyperuniform upon reaching equilibrium, the stable configuration that particles settle into of their own accord. In these equilibrium systems, it is mutual repulsions between the particles that space them apart and give rise to global hyperuniformity. Similar math might explain the emergence of hyperuniformity in bird eyes, the distribution of eigenvalues of random matrices, and the zeros of the Riemann zeta function — cousins of the prime numbers.
The other class is not as well understood. In these “nonequilibrium” systems, which include shaken marbles, emulsions, colloids and ensembles of cold atoms, particles bump into one another but otherwise do not exert mutual forces; external forces must be applied to the systems to drive them to a hyperuniform state. Within the nonequilibrium class, there are further, intractable divisions. Last fall, physicists led by Denis Bartolo of the École Normale Supérieure in Lyon, France, reported in Physical Review Letters that hyperuniformity can be induced in emulsions by sloshing them at the exact amplitude that marks the transition between reversibility and irreversibility in the material: When sloshed more gently than this critical amplitude, the particles suspended in the emulsion return to their previous relative positions after each slosh; when sloshed harder, the particles’ motions do not reverse. Bartolo’s work suggests a fundamental (though not fully formed) connection between the onset of reversibility and the emergence of hyperuniformity in such nonequilibrium systems. Maximally random jammed packings, meanwhile, are a whole different story. “Can we connect the two physics?” Bartolo said. “No. Not at all. We have absolutely no idea why hyperuniformity shows up in these two very different sets of physical systems.”
As they strive to link these threads, scientists have also encountered surprising properties of hyperuniform materials — behaviors that are normally associated with crystals, but which are less susceptible to fabrication errors, more like properties of glass and other uncorrelated disordered media. In a paper expected to be published this week in Optica, French physicists led by Rémi Carminati report that dense hyperuniform materials can be made transparent, whereas uncorrelated disordered materials with the same density would be opaque. The hidden order in the particles’ relative positions causes their scattered light to interfere and cancel out. “The interferences destroy scattering,” Carminati explained. “Light goes through, as if the material was homogeneous.” It’s too early to know what dense, transparent, noncrystalline materials might be useful for, Carminati said, but “there are certainly potential applications,” particularly in photonics.
And Bartolo’s recent finding about how hyperuniformity is generated in emulsions translates into an easy recipe for stirring concrete, cosmetic creams, glass and food. “Whenever you want to disperse particles inside a paste, you have to deal with a hard mixing problem,” he said. “This could be a way to disperse solid particles in a very uniform fashion.” First, you identify a material’s characteristic amplitude, then you drive it at that amplitude a few dozen times, and an evenly mixed, hyperuniform distribution emerges. “I should not tell you this for free, but rather start a company!” Bartolo said.
Salvatore Torquato, a chemist at Princeton University, has studied hyperuniformity since the early 2000s.
Courtesy of Salvatore Torquato
Torquato, Steinhardt and associates have already done so. Their start-up, Etaphase, will manufacture hyperuniform photonic circuits — devices that transmit data via light rather than electrons. The Princeton scientists discovered a few years ago that hyperuniform materials can have “band gaps,” which block certain frequencies from propagating. Band gaps enable controlled transmission of data, since the blocked frequencies can be contained and guided through channels called waveguides. But band gaps were once thought to be unique to crystal lattices and direction-dependent, aligning with the crystal’s symmetry axes. This meant photonic waveguides could only go in certain directions, limiting their use as circuits. Since hyperuniform materials have no preferred direction, their little-understood band gaps are potentially much more practical, enabling not only “wiggly waveguides, but waveguides as you wish,” Steinhardt said.
As for the pattern of five-color mosaics in birds’ eyes, termed “multihyperuniform,” it is, so far, unique in nature. Corbo still hasn’t pinpointed how the pattern forms. Does it emerge from mutual repulsions between cone cells, like other systems in the equilibrium class? Or do cones get shaken up like a box of marbles? His guess is the former. Cells can secrete molecules that repel cells of the same type but have no effect on other types; probably, during embryonic development, each cone cell signals that it is differentiating as a certain type, preventing neighboring cells from doing the same. “That’s a simple model of how this could develop,” he said. “Local action around each cell is creating a global pattern.”
Aside from chickens (the most readily available fowl for laboratory study), the same multihyperuniform retinal pattern has turned up in the three other bird species that Corbo has investigated, suggesting that the adaptation is widespread and not tailored to any particular environment. He wonders whether evolution might have found a different optimal configuration in nocturnal species. “That would be super interesting,” he said. “It’s trickier for us to get our hands on, say, owl eyes.”
This article was reprinted on Wired.com.