Seeing Time Through a Liquid Crystal Display
Time is one of the most fascinating and mysterious subjects in physics. In June, about 60 experts gathered to discuss the nature of time at the Time in Cosmology conference, as Dan Falk reported in Quanta. Some of the questions they considered included: What makes the arrow of time push forward inexorably from the past to the present to the future? Why is the time we call “now” so special to us in the real world, but not at all special in any way in physics? Why does entropy, the technical measure of the amount of disorder in the universe, increase as time moves forward, as the second law of thermodynamics dictates, even though the equations of physics are time-reversible? The contradictory qualities of the many ideas, models, suggestions and speculations presented at the conference highlight how little even the experts understand these fundamental questions.
Since a little hands-on modeling might give us a better appreciation of the issues, I thought we should do a very simple simulation of a toy universe ourselves. But first, let’s look at some ideas we can explore.
One of the motivations for the Time in Cosmology conference was the dissatisfaction felt by some physicists, including co-organizer Lee Smolin, with the standard “block universe” of physics — a static four-dimensional block of space-time in which the flow of time is mere illusion, and in which the future already exists. Smolin rejects this frozen block universe; in his latest book, Time Reborn, he presents arguments in favor of the commonsense view that time flows toward an open-ended future.
While Smolin is known to have iconoclastic views on a lot of modern physics, there are two general ideas of his that I agree with wholeheartedly. The first one, as I pointed out in my “Is Infinity Real?” solution column, is that the mathematical models used in physics are merely mental constructions and cannot be expected to encompass all of physical reality: The map is not the territory. The second is the idea that the Darwinian principle of natural selection is the only underlying source for the truly novel complexity we find not just in the biological world but everywhere in the universe. Smolin has applied this latter idea to his speculative theory of “cosmological natural selection,” which he explains in this short video.
You do not have to subscribe to Smolin’s full-blown theory of cosmological natural selection to see how a simple form of “natural selection” can apply to nonbiological processes such as the creation of stars, galaxies and chemical compounds. This idea, called stratified stability, was expounded almost 50 years ago by Jacob Bronowski, the author of the BBC documentary series The Ascent of Man. Biological natural selection requires random variability of offspring, which causes differences in fitness, resulting in differential survival and reproduction. Stratified stability, on the other hand, simply requires that random combinations of nonliving elements, such as atoms or molecules, form more complex structures, some of which, thanks to forces like gravity or electromagnetism, are more stable than others. These stable structures, whether physical aggregations or chemical compounds, “survive” to form even more complex structures, of which again the most stable persist, thus giving rise to layers upon layers of complex structures and varied chemistry, all formed by the nonbiological “natural selection” of inherent stability. In fact, this process, in principle, can explain how large aggregations like galaxies, stars and planets can form due to gravity and how the chemicals required for life could have originated by prebiotic chemical evolution.
With these ideas in mind, let me describe the rules of my toy universe.
Space: The entire universe consists of a 5-by-6 grid of nodes (4-by-5 cells), as shown.
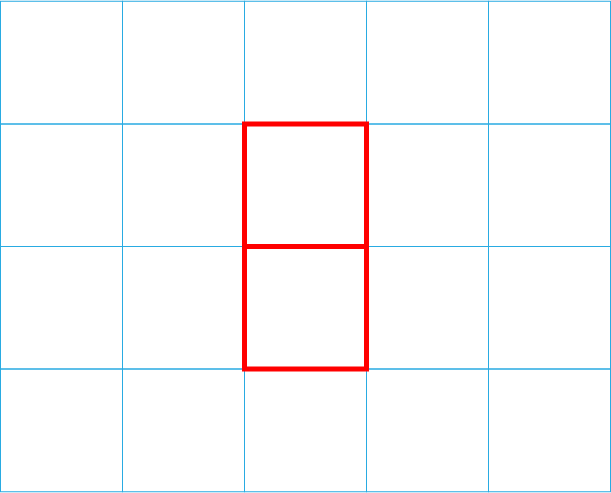
Atoms: The universe is populated by seven red bars, each one unit long, which span two neighboring nodes on the grid horizontally or vertically.
“Central Galaxy” or LCD: The central 3-by-2 portion of this universe can be thought of as the familiar seven-segment liquid crystal display (LCD) from an old-fashioned calculator.
Initial State: The bars are all arranged on the seven segments of the central LCD to form the number “8.”
Dynamic Laws: Every second, all the bars move randomly as follows: One of the two ends of each bar moves to a new position, picked at random from among the neighbors of the node it was on (like a random walk, but constrained by the grid’s border). The other end of the bar follows randomly to one of the neighbors of the new position.
Entropy (Measure of Disorder): The system is considered to be most orderly if all the segments of the central LCD are occupied. The “entropy” of this initial state is zero. Maximum entropy is achieved when no bars touch any of the nodes of the central LCD “8.”
The value of the entropy is calculated as follows. Count the numbers of the following: unoccupied central LCD segments (u); the number of bars fully occupying a segment of the central LCD (there may be more than one bar occupying the same segment) (b); the number of bars touching a node of the central LCD but otherwise outside it (t). Then calculate the entropy using the formula (14 + 4u – 2b – t)/42. Why divide by 42? Well, that’s the secret of the universe, don’t you know?
Obviously, this model can be modified and improved in many ways, but I was aiming for something that had enough complexity to tell us something interesting, while at the same time remaining simple enough to allow for intelligent guessing and estimation regarding its evolution. To those of you who enjoy simulations and have the interest, skills and time to do it, you are welcome to do so. Please share your simulations and insights with us! For the rest of you, we may post a downloadable file within a couple of weeks that will allow you to play with the model yourselves.
For now, try to guess or estimate the answer to the questions below. It’ll be fun to compare the answers to the results of the simulations.
Question 1:
Here’s a passage from Dan Falk’s article, where he talks about how entropy increases in the real universe and why a whole object does not spontaneously re-form from its pieces.
Scrambled eggs always come after whole eggs, never the other way around. To make sense of this, physicists have proposed that the universe began in a very special low-entropy state. In this view … entropy increases because the Big Bang happened to produce an exceptionally low-entropy universe. There was nowhere to go but up.
An analogue of the egg in our toy universe is the central number formed on the LCD. From the initial zero-entropy state, how long do you think it will take to get to the completely “scrambled” or maximum-entropy state? What will be the approximate value of the entropy when the universe reaches a “steady state”? How long will this take? Can it ever get back to the original minimal-entropy or “whole egg” state? If so, how long do you think this scenario will take?
Question 2:
Let’s introduce stratified stability into our universe, by adding the following rule: If a bar lands on an unoccupied segment of the central LCD, the bar stops moving and occupies that position permanently. The initial state of the universe is also different: Let’s assume that it is the most disordered state (maximum entropy), where none of the bars are touching the central LCD.
From this disordered start, how long do you think it will take to reach the minimum-entropy state and form the number 8 on the LCD? Assume that the movement rules are the same as before — one move per second.
Question 3:
In the universe of question 2, of the following three shapes that could appear on the LCD — the numbers 6 and 9 and the letter A — which one is most likely to be the last step before the number 8 is reached? Which is least likely?
Question 4:
Leaving aside my jocular reference to the number 42, can you figure out the rationale behind the entropy calculation?
Suggested puzzle enhancements are welcome. Did this exercise stimulate any ideas or conclusions?
Happy puzzling. Have fun simulating the universe and unscrambling eggs!
Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt. And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION” (it will not appear online, so solutions to the puzzle above should be submitted separately).
Note that we may hold comments for the first day or two to allow for independent contributions by readers.
Update: The solution has been published here.




