Biodiversity May Thrive Through Games of Rock-Paper-Scissors
Some species seem to compete in a kind of rock-paper-scissors game in which no one species enjoys a lasting dominance. It may be part of why nature can maintain so much biodiversity.
Camille Chew for Quanta Magazine
Introduction
A pioneer of synthetic biology at the University of California, San Diego, Jeff Hasty has spent his 20-year career designing strategies to make genetic circuits in engineered bacteria work together. But several years ago, Hasty had to admit that even he couldn’t outfox the humble bacterium Escherichia coli.
Hasty didn’t have a problem engineering useful, tightly regulated new genetic traits or getting them to work in cells. That was the easy part. What’s harder, he discovered, is maintaining those traits. If a cell needs to divert some of its resources to make a desired protein, it becomes marginally less fit than cells that don’t synthesize it. Inevitably, cells acquire mutations deactivating the introduced genetic circuitry, and the mutants quickly replace the original cells. As a result, the desired characteristic disappears, often within 36 hours.
“It’s not a matter of if, it’s a matter of when,” Hasty said.
For years, Hasty watched mutant E. coli disable even his elegantly engineered systems. But last September in Science, Hasty, his doctoral student Michael Liao and their colleagues designed a strategy to thwart even the most mutation-happy bacterium through a kind of “microbial peer pressure,” as an accompanying commentary called it. The UCSD team used three engineered strains of E. coli that worked in tandem. Each strain produced a toxin, a corresponding antitoxin to protect itself, and a second antitoxin for protection against one of the other strains. The first strain could kill the second but not the third; the second could kill the third but not the first; the third could kill the first but not the second.
This round robin of antagonism meant that, by sequentially adding the strains of bacteria, the researchers could keep the numbers of engineered E. coli high while ensuring that unhelpful mutants were snuffed out by the newcomers’ toxins. The ecological interaction of the cells stabilized the system.
The project was nearing completion when Liao stumbled across the fact that other scientists were already paying attention to this strategy. Researchers in ecology and evolution had wrestled with it for decades as one possible answer to a major question in their field: How does so much biodiversity survive in nature? But even aside from its scientific history, the strategy is better known as a game used by children around the world to settle playground squabbles.
The game is rock-paper-scissors, “a classic game in game theory and evolutionary theory,” said the mathematical biologist Barry Sinervo of the University of California, Santa Cruz, whose field studies on side-blotched lizards helped to establish its relevance to ecosystems.
The rules of the game are easy: Rock beats scissors, scissors beat paper, and paper beats rock. No player has an advantage, and the chances of winning are equal regardless of what item they pick. When two people play, there’s always a clear victor. Add in more players, however, and the game becomes more complex, with the success of different strategies often cyclically rising and falling.
Biologists studying rock-paper-scissors have modeled how the game plays out with scores or even hundreds of species. They have also investigated how it changes when the species interact in various landscapes, and when the species differ in their mobility and competitiveness. What they have found is that over time, rock-paper-scissors may enable many species to coexist in the same area by cycling in and out of dominance.
Scientists are still determining the true importance of the game to living systems, but their discoveries have implications that could affect evolutionary theory, our understanding of ecological dynamics, biotechnology, and conservation policy. “It’s a universal game, which is pretty darn neat,” Sinervo said. “Rock-paper-scissors covers the entire biological universe.”
Equations of Abundance
When Charles Darwin published his theory of natural selection in 1859, he and his contemporaries hypothesized that competition between individuals provided the force behind evolution. More than 150 years of experiments following Darwin’s initial work confirmed that competition is indeed a major evolutionary force. There is just one problem.
If simplistic competition were the only evolutionary force, then after billions of years, only a handful of highly competitive species should be left. Instead, the planet is home to a staggering array of life. The number of species for which Earth is home is almost impossible to estimate; one recent attempt pegged it at about 2 billion, but earlier efforts ranged from under 10 million to 1 trillion. The lowland Amazon rainforests alone are home to more than 6,700 tree species and 7,300 other seed plant species — numbers that don’t begin to account for the accompanying insects, mammals, fungi and microbes.
“We look around and there are thousands, even millions, of microbes living in one hectare of forest,” said Daniel Maynard, an ecologist at the Swiss Federal Institute of Technology Zurich. “And no matter what you do, they all survive. It’s not like one tears through the community and beats out everything else.”
One of the first breakthroughs in explaining biodiversity came not from ecology but from mathematics. In 1910, the American biophysicist and statistician Alfred Lotka developed a series of equations to describe certain chemical reactions. By 1925, he had realized that the same equations could be adapted to describe the cyclic rise and fall of predator and prey populations. A year later, the Italian mathematician and physicist Vito Volterra independently developed the same set of equations.
Their work showed how the number of predators depends on the number of prey. That insight might seem obvious, says Margaret Mayfield, an ecologist at the University of Queensland in Australia, but the equations of Lotka and Volterra were groundbreaking in their time because they gave ecologists a way to start measuring and modeling the natural world.
Still, the equations weren’t perfect. They rested on useful but simplistic assumptions, and they couldn’t represent relationships between species that weren’t predator and prey but competed for resources.
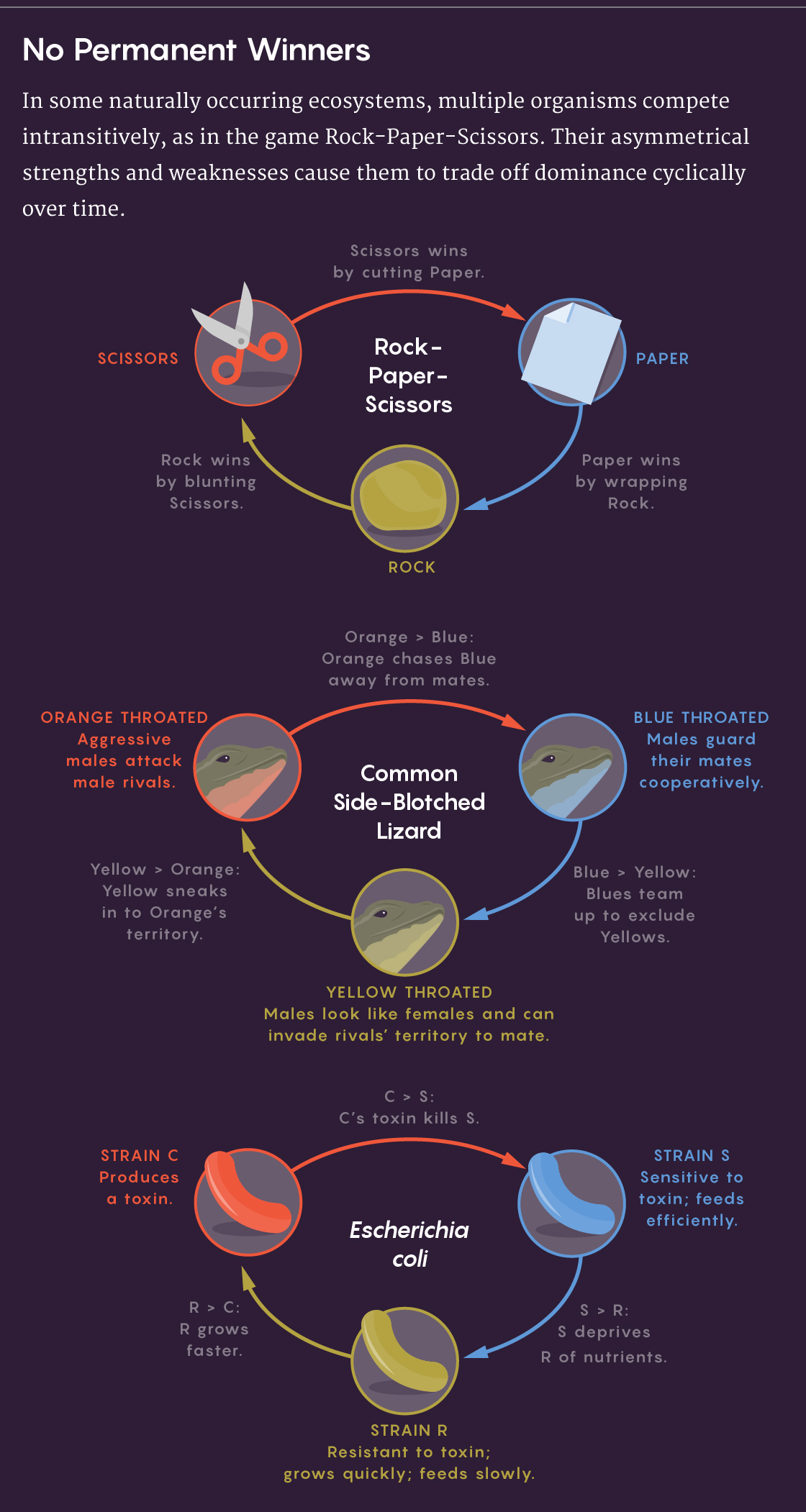
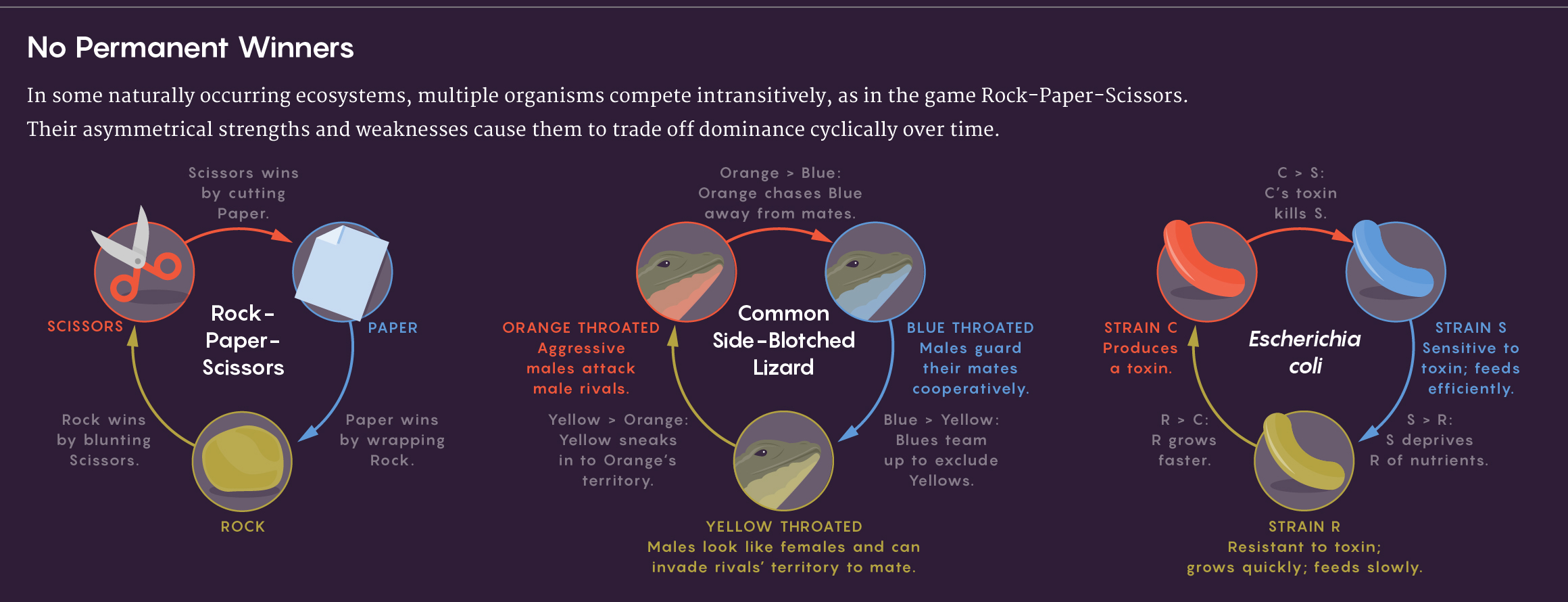
That began to change in 1975, however, when the mathematicians Robert May and Warren Leonard adapted the classic Lotka-Volterra equations for what ecologists call intransitive competition. When competition is transitive, it’s hierarchical: If A beats B and B beats C, then A also beats C, making A the winner in any contest. Intransitive competition lacks this hierarchy, because C can beat A. Instead of staying a clear winner, A will dominate for a while but then give way to C, which then gives way to B, followed once again by the rise of A.
What May and Leonard created was in effect the math to describe rock-paper-scissors in ecology. Later mathematicians extended their work to show that these intransitive relationships could involve a nearly infinite number of species.
Think of it like a gladiator death match, Maynard said. In single combat against a skilled fighter, he said, “I’m going to lose.” But if he were in a group of 100 fighters, he said, other defensive options might be available, such as forming an alliance with a stronger fighter. That strategy might help him outlast his competitors and come out on top.
Mating Games
In the 1970s and ’80s, scientists began to document real-life examples in papers that showed rock-paper-scissors relationships among organisms living on coral reefs and among strains of the common yeast Saccharomyces cerevisiae. Among the most famous studies, however, was Sinervo’s work on the common side-blotched lizard, published in Nature in 1996.

Male common side-blotched lizards with blue throats, like this one, band together to guard their females cooperatively. Other competing forms of this lizard with orange and yellow throats use different strategies.
At first glance, the common side-blotched lizard lives down to its humble name. It’s small, brown and finger-length, and its main distinguishing characteristics are the patterns on its back and a spot of color on its throat. The lizards’ mating system, however, is far more unusual. In 1990, Sinervo traveled to the heart of side-blotched lizard territory, on the slopes of California’s parched Inner Coast Range, just outside the city of Merced. Sinervo spent five years studying how male lizards convince their lady friends to swipe right — and how they get their rivals to stay away.
A male’s mating strategy, Sinervo knew, was indicated by the patch of color on its throat. Lizards with orange throats are ultra-competitive. They individually guard large harems of females and attack any trespassing male rivals. Blues cooperate with each other to guard their territory and mates, a strategy that is only somewhat effective against the oranges. But it makes them less susceptible to the sneaky yellows, which mimic the appearance of sexually mature females and sneak into orange males’ territory to mate without fear of competition.
Sinervo noticed that at his study site, each color dominated for a year or two, after which a specific rival took over: Blue gave way to orange, which gave way to yellow, which gave way to blue once again. Some locations might have just a single color, but Sinervo never saw just two colors together, because one always completely replaced the other. But with three, the populations oscillated in dominance. When Sinervo and a colleague later began writing out equations to describe the observations, they soon realized they were describing a form of rock-paper-scissors.
Other situations in nature where this game theory seems to guide evolution have come to light. In the February 2020 issue of The American Naturalist, for instance, Sinervo and his colleagues describe how it explains the prevalence of particular mating strategies among 288 species of rodents — and why certain species are more or less likely to be promiscuous, polygynous or monogamous.
Still, observations from nature can only tell scientists so much. To understand what types of environments create these rock-paper-scissors games between species and whether the new equations can help explain biodiversity, scientists had to go back to the lab.
Local Environments Change the Game
The bacterium E. coli gets a bad rap as a mundane colon dweller. Yet over the years, microbiologists have identified hundreds of E. coli strains with diverse properties. One family carries a group of genes named Col, which produces a toxin called colicin but also a protein that protects the bacterium against it. Some E. coli strains are sensitive to colicin, and others have evolved mutations that make them resistant. Resistant strains (known as R) grow faster than colicin-producing (C) strains because they don’t have the cost of producing colicin. Sensitive (S) strains can outcompete R because the protective mutations also impair the cells’ ability to transport nutrients. This system creates a perfect rock-paper-scissors setup, since R beats C, C beats S, and S beats R.
About two decades ago, microbiologists at Stanford University had the bacteria play rock-paper-scissors in three different situations: a flask where they all mixed together; a static petri dish where they were grouped together with limited movement; and a “mixed plate” environment where they had more intermediate mobility. In their Nature paper in 2002, Benjamin Kerr (now at the University of Washington), Brendan Bohannan (now at the University of Oregon), and their colleagues found that in both the flask and the distributed plate, the R strain quickly won out over both the S and C groups.
The static petri dish, however, told a different story. When Kerr and Bohannan analyzed photographs of the bacterial colonies growing there, they saw a game of rock-paper-scissors playing out where the different strains came into contact, just as theory predicted. These results showed that local environments play a crucial role not only in the emergence of rock-paper-scissors, but in the consequent appearance and maintenance of biodiversity, explained Stefano Allesina, a theoretical ecologist at the University of Chicago.
Lucy Reading-Ikkanda/Quanta Magazine
Reading this paper as a graduate student, Allesina found it “mind-blowing.” He picked the study for his journal club and posed a rhetorical question to his fellow students: Could rock-paper-scissors work with as many as 70 strains of E. coli?
Because that discussion question stuck in his brain, Allesina decided to focus his work on developing computational models that could simulate rock-paper-scissors for large numbers of players. He found that adding more species to his model bolstered the system’s stability, making it less likely that any individual population would go extinct. Maynard reached the same conclusion in his research: Biodiversity begets more biodiversity as a simple result of the system’s stability because large numbers of organisms can coexist.
This interdependence is part of what makes intransitivity so very common, according to Maynard. “You can’t be great at everything,” he said. “That genetically just can’t exist.” Each species has an Achilles’ heel that leaves the way open for rock-paper-scissors effects, which make every species vulnerable but also offer some relief from overwhelming predation. More diverse systems have higher levels of intransitivity and stability.
“It’s hard to reconcile a very unstable world with what we’re seeing in nature,” Allesina said. And as the diversity of a system increases, it offers more ways for species to interact, which can also lead to greater coexistence and biodiversity.
Tristan Ursell at the University of Oregon, inspired by Kerr and Bohannan’s work, wanted to take it one step further. Although their study had shown that the distribution of organisms was key to the development of rock-paper-scissors, the environments in their experiments didn’t have physical barriers that would prevent the bacteria from moving about. The natural world is nothing like that: Whether a microbe is living on a plant’s roots or snuggled up somewhere in our intestines, its environment is filled with obstructions. Ursell, a biophysicist rather than a microbiologist, decided to create a series of computer models to see how physical obstacles could alter the rock-paper-scissors cycles.
Going into the project, Ursell expected that the obstacles might have minor consequences for the simulation. “I did not anticipate that it would in some cases completely flip over the stability,” he said.
Why Saving Single Species Isn’t Enough
Pitting two species against each other in an open space, for example, typically ended with one replacing the other. But if the landscape in Ursell’s computer model had barriers, both species could often coexist. Meanwhile, three species locked in a rock-paper-scissors game in an open space could coexist by cycling in and out of dominance. Introducing a barrier into their world often led to one species eliminating the others.
Ursell’s resulting paper with Nick Vallespir Lowery, published online in December 2018 by the Proceedings of the National Academies of Science, joined other work showing the hidden complexities of real-life rock-paper-scissors games. For example, a team of scientists led by Erwin Frey and Marianne Bauer at the Ludwig Maximilian University of Munich created mathematical models of soil microbes, which obtain nutrients and water via small openings in the soil itself, holes that also allow them to interact with their neighbors. If you try to grow soil-dwelling microbes in the laboratory, the species that can reproduce the fastest wins out. Yet in nature, a single gram of soil can contain more than 10,000 types of microbes.
The secret, Frey and Bauer found, is the amount of time is takes for the bacteria to adapt to changing environmental conditions. Because of this constraint, and the connectivity built into soil’s complex physical structure, thousands of microbes can continue to coexist.
This feedback between ecology and evolution is crucial, said Swati Patel, an applied mathematician at Tulane University, because these interactions can lead to either ecosystem stability or extinction, as her mathematical work in The American Naturalist showed. If species A starts to go extinct, she explained, species B might evolve in such a way that A can recover. This idea also works in reverse.
“Our human impact on various ecosystems can … make species evolve in ways we hadn’t anticipated,” Patel said.
Long-term ecological stability and coexistence doesn’t mean that population numbers will remain the same. Fluctuations are built into these models, Patel said. But how widely they vary and how quickly is key.
Daniel Stouffer, an ecologist at the University of Canterbury in New Zealand and a frequent collaborator with Mayfield, says that weaker interactions help keep fluctuations between species from becoming too extreme. Ecologists call this the storage effect. “A species doesn’t always have to be the best. It just has to have enough times where it can be sufficiently good that it can weather the bad years,” Stouffer said.
If the numbers of one species drop too low, a chance event like a disease outbreak or drought can cause it to go extinct. These extinctions open a vacuum in an ecosystem, which can create an extinction cascade or open space for other organisms to recover. These ripple effects also provide clues for conservation biologists working to save endangered organisms. According to Allesina, theoretical work in rock-paper-scissors shows that ecologists may need to focus on saving entire ecosystems instead of just individual species.
“Imagine that you only want to conserve the rock of the rock-paper-scissor [trio],” he said. You might not care about the paper or the scissors, but as soon as one goes extinct, that “could reverberate through these networks of interactions to other species that you would never have guessed.”
Despite the advances in theoretical work that describes how rock-paper-scissors might operate in larger ecosystems, Stouffer points out that biologists have documented relatively few examples of these intransitive dynamics in the wild. Models show that they should exist, but identifying where rock-paper-scissors games are likely to dominate remains a challenge for evolutionary game theorists.
Maynard says that the best way forward may be for scientists to take their cues from nature itself. He has begun to develop a new statistical approach that might enable him to infer how species interact and to identify emergent patterns in those interactions. But he says that the key will be to remember that rock-paper-scissors is only one piece of a larger biodiversity puzzle, and that constant change — whether via gene mutation and evolution or natural shifts in climate — is the rule.



