Black Hole Paradoxes Reveal a Fundamental Link Between Energy and Order
Introduction
“Physicists like to probe the extreme,” said Garrett Goon, a physicist at Carnegie Mellon University. “The fact that you can’t go further, that something is changing, something is blocking you — something interesting is happening there.”
For decades, black holes have played the headlining role in the thought experiments that physicists use to probe nature’s extremes. These invisible spheres form when matter becomes so concentrated that everything within a certain distance, even light, gets trapped by its gravity. Albert Einstein equated the force of gravity with curves in the space-time continuum, but the curvature grows so extreme near a black hole’s center that Einstein’s equations break. Thus generations of physicists have looked to black holes for clues about the true, quantum origin of gravity, which must fully reveal itself in their hearts and match Einstein’s approximate picture everywhere else.
Plumbing black holes for knowledge of quantum gravity originated with Stephen Hawking. In 1974, the British physicist calculated that quantum jitter at the surfaces of black holes cause them to evaporate, slowly shrinking as they radiate heat. Black hole evaporation has informed quantum gravity research ever since.
More recently, physicists have considered the extreme of the extreme — entities called extremal black holes — and found a fruitful new problem.
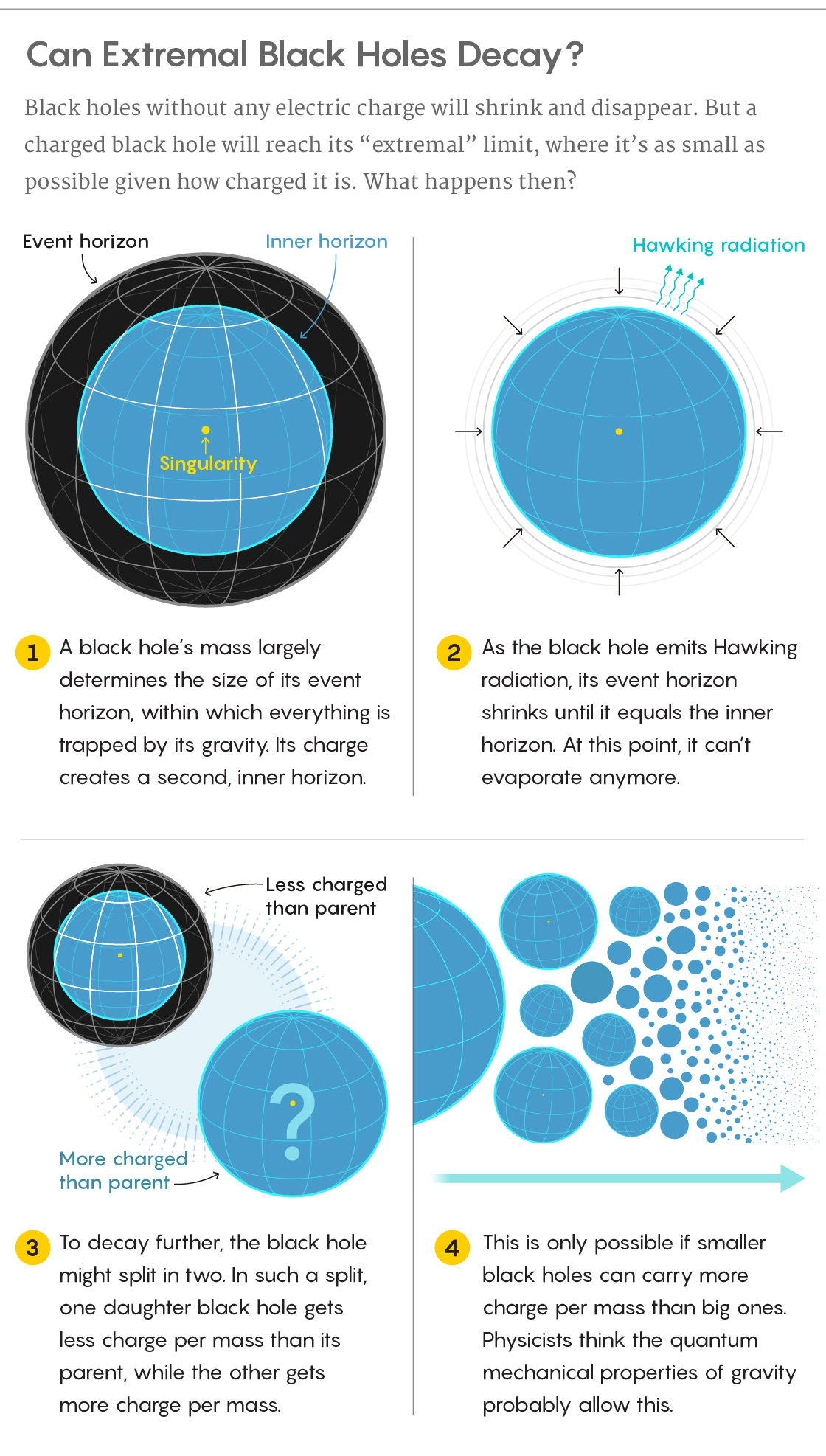
Black holes become electrically charged when charged stuff falls into them. Physicists calculate that black holes have an “extremal limit,” a saturation point where they store as much electric charge as possible for their size. When a charged black hole evaporates and shrinks in the manner described by Hawking, it will eventually reach this extremal limit. It’s then as small as it can get, given how charged it is. It can’t evaporate further.
But the idea that an extremal black hole “stops radiating and just sits there” is implausible, said Grant Remmen, a physicist at the University of California, Berkeley. In that case, the universe of the far future will be littered with tiny, indestructible black hole remnants — the remains of any black holes that carry even a touch of charge, since they’ll all become extremal after evaporating enough. There’s no fundamental principle protecting these black holes, so physicists don’t think they should last forever.
So “there is a question,” said Sera Cremonini of Lehigh University: “What happens to all these extremal black holes?”
Physicists strongly suspect that extremal black holes must decay, resolving the paradox, but by some other route than Hawking evaporation. Investigating the possibilities has led researchers in recent years to major clues about quantum gravity.
Four physicists realized in 2006 that if extremal black holes can decay, this implies that gravity must be the weakest force in any possible universe, a powerful statement about quantum gravity’s relationship to the other quantum forces. This conclusion brought greater scrutiny to extremal black holes’ fates.
Then, two years ago, Remmen and collaborators Clifford Cheung and Junyu Liu of the California Institute of Technology discovered that whether extremal black holes can decay depends directly on another key property of black holes: their entropy — a measure of how many different ways an object’s constituent parts can be rearranged. Entropy is one of the most studied features of black holes, but it wasn’t thought to have anything to do with their extremal limit. “It’s like, wow, OK, two very cool things are connected,” Cheung said.
In the latest surprise, that link turns out to exemplify a general fact about nature. In a paper published in March in Physical Review Letters, Goon and Riccardo Penco broadened the lessons of the earlier work by proving a simple, universal formula relating energy and entropy. The newfound formula applies to a system such as a gas as well as a black hole.


Riccardo Penco (top) and Garrett Goon used extremal black holes to prove a universal connection between energy and entropy.
Riccardo Penco (left) and Garrett Goon used extremal black holes to prove a universal connection between energy and entropy.
Carnegie Mellon University; Christine Goon
With the recent calculations, “you really are learning about quantum gravity,” Goon said. “But maybe even more interesting, you’re learning something about more everyday stuff.”
Black Holes at the Extreme
Physicists see very easily that charged black holes reach an extremal limit. When they combine Einstein’s gravity equations and the equations of electromagnetism, they calculate that a black hole’s charge, Q, can never surpass its mass, M, when both are converted into the same fundamental units. Together, the black hole’s mass and charge determine its size — the radius of the event horizon. Meanwhile, the black hole’s charge also creates a second, “inner” horizon, hidden behind the event horizon. As Q increases, the black hole’s inner horizon expands while the event horizon contracts until, at Q = M, the two horizons coincide.
If Q increased further, the radius of the event horizon would become a complex number (involving the square root of a negative number), rather than a real one. This is unphysical. So, according to a simple mashup of James Clerk Maxwell’s 19th-century theory of electromagnetism and Einsteinian gravity, Q = M must be the limit.
When a black hole hits this point, a simple option for further decay would be to split into two smaller black holes. Yet in order for such splitting to happen, the laws of conservation of energy and conservation of charge require that one of the daughter objects must end up with more charge than mass. This, according to Einstein-Maxwell, is impossible.
5W Infographics for Quanta Magazine
But there might be a way for extremal black holes to split in two after all, as Nima Arkani-Hamed, Lubos Motl, Alberto Nicolis and Cumrun Vafa pointed out in 2006. They noted that the combined equations of Einstein and Maxwell don’t work well for small, strongly curved black holes. At smaller scales, additional details related to the quantum mechanical properties of gravity become more important. These details contribute corrections to the Einstein-Maxwell equations, changing the prediction of the extremal limit. The four physicists showed that the smaller the black hole, the more important the corrections become, causing the extremal limit to move farther and farther away from Q = M.
The researchers also pointed out that if the corrections have the right sign — positive rather than negative — then small black holes can pack more charge than mass. For them, Q > M, which is exactly what’s needed for big extremal black holes to decay.
If this is the case, then not only can black holes decay, but Arkani-Hamed, Motl, Nicolis and Vafa showed that another fact about nature also follows: Gravity must be the weakest force. An object’s charge, Q, is its sensitivity to any force other than gravity. Its mass, M, is its sensitivity to gravity. So Q > M means gravity is the weaker of the two.
From their assumption that black holes ought to be able to decay, the four physicists made a more sweeping conjecture that gravity must be the weakest force in any viable universe. In other words, objects with Q > M will always exist, for any kind of charge Q, whether the objects are particles like electrons (which, indeed, have far more electric charge than mass) or small black holes.
This “weak gravity conjecture” has become hugely influential, lending support to a number of other ideas about quantum gravity. But Arkani-Hamed, Motl, Nicolis and Vafa didn’t prove that Q > M, or that extremal black holes can decay. The quantum gravity corrections to the extremal limit might be negative, in which case small black holes can carry even less charge per unit mass than large ones. Extremal black holes wouldn’t decay, and the weak gravity conjecture wouldn’t hold.
This all meant that researchers needed to figure out what the sign of the quantum gravity corrections actually is.
Disorder Everywhere
The issue of quantum gravity corrections has come up before, in another, seemingly unrelated line of black hole study.
Almost 50 years ago, the late physicists Jacob Bekenstein and Stephen Hawking independently discovered that a black hole’s entropy is directly proportional to its surface area. Entropy, commonly thought of as a measure of disorder, counts the number of ways an object’s internal parts can be rearranged without any change to its overall state. (If a room is messy, or high entropy, for instance, you can move objects around at random and it will stay messy; by contrast, if a room is tidy, or low entropy, moving things around will make it less tidy.) By building a bridge between a black hole’s entropy, which concerns its inner microscopic ingredients, and its geometric surface area, Bekenstein and Hawking’s entropy area law has become one of physicists’ strongest footholds for studying black holes and quantum gravity.
Bekenstein and Hawking deduced their law by applying Einstein’s gravity equations (together with the laws of thermodynamics) to the black hole’s surface. They treated this surface as smooth and ignored any structure that exists over short distances.
In 1993, the physicist Robert Wald of the University of Chicago showed that it’s possible to do better. Wald found clever tricks for inferring the small effects that emanate from more microscopic levels of reality, without knowing what the complete description of that deeper level of reality is. His tactic, pioneered in a different context by the theoretical physicist Kenneth Wilson, was to write down every possible physical effect. To Einstein’s equations, Wald showed how to add a series of extra terms — any terms that have the right dimensions and units, constructed of all physically relevant variables — that might describe the unknown short-distance properties of a black hole’s surface. “You can write down the most general set of terms that you could have in principle that describe [black hole] curvatures of a certain size,” said Cremonini.

Fortunately, the series can be truncated after the first several terms, since increasingly complicated composites of many variables contribute little to the final answer. Even many of the leading terms in the series can be crossed out because they have the wrong symmetries or violate consistency conditions. This leaves just a few terms of any significance that modify Einstein’s gravity equations. Solving these new, more complicated equations yields more exact black hole properties.
Wald went through these steps in 1993, calculating how short-distance quantum gravitational effects correct the Bekenstein-Hawking entropy area law. These corrections shift a black hole’s entropy so that it’s not exactly proportional to area. And while it’s not possible to calculate the entropy shift outright — variables with unknown values are involved — what’s clear is that the corrections grow more significant the smaller the black hole, and therefore so does the entropy shift.
Three years ago, Cheung, Liu and Remmen applied Wald’s same basic approach to the study of charged black holes and the extremal limit. They modified the Einstein-Maxwell equations with a series of extra terms coming from short-distance effects, and they solved the new equations to calculate the new, corrected extremal limit. To their surprise, they recognized the answer: The corrections to the extremal limit of a charged black hole exactly match the corrections to its entropy, as calculated from Wald’s formula; quantum gravity unexpectedly shifts both quantities in the same way.
Remmen remembers the date when they completed the calculation — November 30, 2017 — “because it was that exciting,” he said. “That’s a very deep and exciting thing that we proved, that these [extra] terms give a shift in entropy and extremality that are equal to each other.”



Grant Remmen, Clifford Cheung and Junyu Liu (from top) found that the change in a black hole’s extremal limit matches its change in entropy.
Grant Remmen, Clifford Cheung and Junyu Liu (from left) found that the change in a black hole’s extremal limit matches its change in entropy.
Vincent Su, UC Berkeley; Meimei Dong; Caltech
But do the matching shifts go in the right direction? Both corrections depend on undetermined variables, so they could in principle be either positive or negative. In their 2018 paper, Cheung and company calculated that the entropy shift is positive in a large class of scenarios and models of quantum gravity. They argue that it also makes intuitive sense that the entropy shift should be positive. Recall that entropy measures all the different possible internal states of a black hole. It seems reasonable that accounting for more microscopic details of a black hole’s surface would reveal new possible states and thus lead to more entropy rather than less. “The truer theory will have more microstates,” Remmen said.
If so, then the shift in the extremal limit is also positive, allowing smaller black holes to store more charge per mass. In that case, “black holes can always decay to lighter ones,” Cheung said, and “the weak gravity conjecture is true.”
But other researchers stress that these findings do not constitute an outright proof of the weak gravity conjecture. Gary Shiu, a theoretical physicist at the University of Wisconsin, Madison, said the belief that entropy should always increase when you take quantum gravity into account is “an intuition that some might have, but it’s not always true.”
Shiu has identified counterexamples: unrealistic models of quantum gravity in which, through cancellations, short-distance effects decrease black holes’ entropy. These models violate causality or other principles, but the point, according to Shiu, is that the newfound connection to entropy doesn’t prove all by itself that extremal black holes can always decay, or that gravity is always the weakest force.
“To be able to prove [the weak gravity conjecture] would be fantastic,” Shiu said. “That’s a lot of why we’re still thinking about this problem.”
The Forbidden Swampland
Gravity is the weakest of the four fundamental forces in our universe. The weak gravity conjecture says it couldn’t have been otherwise. Aside from our universe, the conjecture also appears to hold in all possible theoretical universes derived from string theory. A candidate for the quantum theory of gravity, string theory posits that particles aren’t points but rather extended objects (nicknamed strings), and that space-time, close-up, also has extra dimensions. When string theorists write down different sets of strings that might define a universe, they invariably find that gravity — which arises from a type of string — is the weakest force in these model universes. “Seeing how this ends up panning out in case after case after case after case is very striking,” said Jorge Santos, a physicist at the Institute for Advanced Study in Princeton, New Jersey, and the University of Cambridge.
The weak gravity conjecture is one of the most important in a network of “swampland conjectures” posed by physicists in the last two decades — speculative statements, based on thought experiments and examples, about what kinds of universes are and are not possible. By ruling out possibilities (putting impossible universes in a no-go “swampland”), swampland theorists aim to clarify why our universe is the way it is.
If researchers could prove that gravity is inevitably weakest (and that black holes can always decay), the most important implication, according to Santos, is that it means quantum gravity “has to be a theory of unification.” That is, if Q and M must have a fixed ratio, their associated forces must be part of the same unified mathematical framework. Santos noted that “the only theory out there” that unifies the fundamental forces in a single framework is string theory. Rival approaches such as loop quantum gravity attempt to quantize gravity by dividing space-time into pieces, without connecting gravity with the other forces. “If the weak gravity conjecture is correct, things like loop quantum gravity are dead,” said Santos.
Jorge Pullin, a loop quantum gravity theorist at Louisiana State University, sees “dead” as far too strong a word. The approach could itself be part of a larger unified theory, he said: “Loop quantum gravity doesn’t rule out a unification structure, but we haven’t pursued it yet.”

The weak gravity conjecture also mutually reinforces several other swampland conjectures, including statements about the roles of symmetry and distance in quantum gravity. According to Shiu, the logical connection between these conjectures “gives us some confidence that even though these statements are made on a conjectural sense, there may be universal truth behind them.”
Shiu compared our current, conjectural understanding of quantum gravity to the early days of quantum mechanics. “There were a lot of conjectures, a lot of leaps of faith about what is the right theory of the subatomic world,” he said. “Eventually many of these guesses turned out to be part of this much bigger picture.”
Universal Energy and Disorder
The recent research might have implications beyond black holes and quantum gravity.
In their March paper, Goon and Penco redid the calculation of the black hole entropy and extremality corrections. Rather than using the language of gravity and black hole surface geometry, they calculated the corrections purely in terms of universal thermodynamic quantities like energy and temperature. This allowed them to discover a thermodynamic relation between energy and entropy that applies generally in nature.
“It’s a beautiful relation,” said Santos.
In the case of black holes, the duo’s formula says what Cheung, Remmen and Liu already proved: that quantum gravity shifts the extremal limit of black holes (allowing them to store more charge per mass), and it shifts their entropy by a proportional amount. Another way of describing the extra storage capacity coming from quantum gravity is that a black hole of fixed charge can have less mass. Mass is a form of energy, and so this drop in mass can be thought of more generally as a shift in energy — one that is inversely proportional to a shift in entropy.
Whereas for a black hole, the equal and opposite shifts in energy and entropy come from unknown details of quantum gravity, an equivalent situation exists for any physical system near its extremal limit.
A gas, for instance, becomes extremal when cooled to absolute zero. Goon and Penco’s thermodynamic formula says that any changes to the microscopic physics of the gas, such as the type of atoms that comprise it, produce equal and opposite shifts in its energy and entropy. Goon speculated that the relation between energy and entropy might be useful in studies of ultracold gases and other cryogenic experiments, “because sometimes one is easier to calculate than the other.”
Whether this entropy-energy relation ever proves useful in earthly domains of physics, researchers still have plenty more work to do to explore the newfound link in the context of black holes and what it means for the nature of gravity.
“Being able to answer, ‘Why is gravity weak?’” Cheung said. “The fact that that question is even on the board, the fact that that’s a question that one can legitimately answer outside the realm of philosophy, and the fact that it’s connected through this long path to entropy, which is like the tried-and-true, most fascinating thing about black holes, … seems crazy.”
Correction: June 15, 2020
An earlier version of this article referred to “the condensed matter physicist Kenneth Wilson.” While Wilson earned a Nobel Prize for the study of phase transitions, his work spanned many fields, including and especially high-energy particle theory.
This article was reprinted on Wired.com and on Spektrum.de.