Computer Scientists Expand the Frontier of Verifiable Knowledge

By interrogating entangled quantum computers, a person can verify the answers to enormously complicated problems.
xsullo for Quanta Magazine
Introduction
Imagine someone came along and told you that they had an oracle, and that this oracle could reveal the deep secrets of the universe. While you might be intrigued, you’d have a hard time trusting it. You’d want some way to verify that what the oracle told you was true.
This is the crux of one of the central problems in computer science. Some problems are too hard to solve in any reasonable amount of time. But their solutions are easy to check. Given that, computer scientists want to know: How complicated can a problem be while still having a solution that can be verified?
Turns out, the answer is: Almost unimaginably complicated.
In a paper released in April, two computer scientists dramatically increased the number of problems that fall into the hard-to-solve-but-easy-to-verify category. They describe a method that makes it possible to check answers to problems of almost incomprehensible complexity. “It seems insane,” said Thomas Vidick, a computer scientist at the California Institute of Technology who wasn’t involved in the new work.
The research applies to quantum computers — computers that perform calculations according to the nonintuitive rules of quantum mechanics. Quantum computers barely exist now but have the potential to revolutionize computing in the future.
The new work essentially gives us leverage over that powerful oracle. Even if the oracle promises to tell you answers to problems that are far beyond your own ability to solve, there’s still a way to ensure the oracle is telling the truth.
Until the End of the Universe
When a problem is hard to solve but easy to verify, finding a solution takes a long time, but verifying that a given solution is correct does not.
For example, imagine someone hands you a graph — a collection of dots (vertices) connected by lines (edges). The person asks you if it’s possible to color the vertices of the graph using only three colors, such that no connected vertices have the same color.
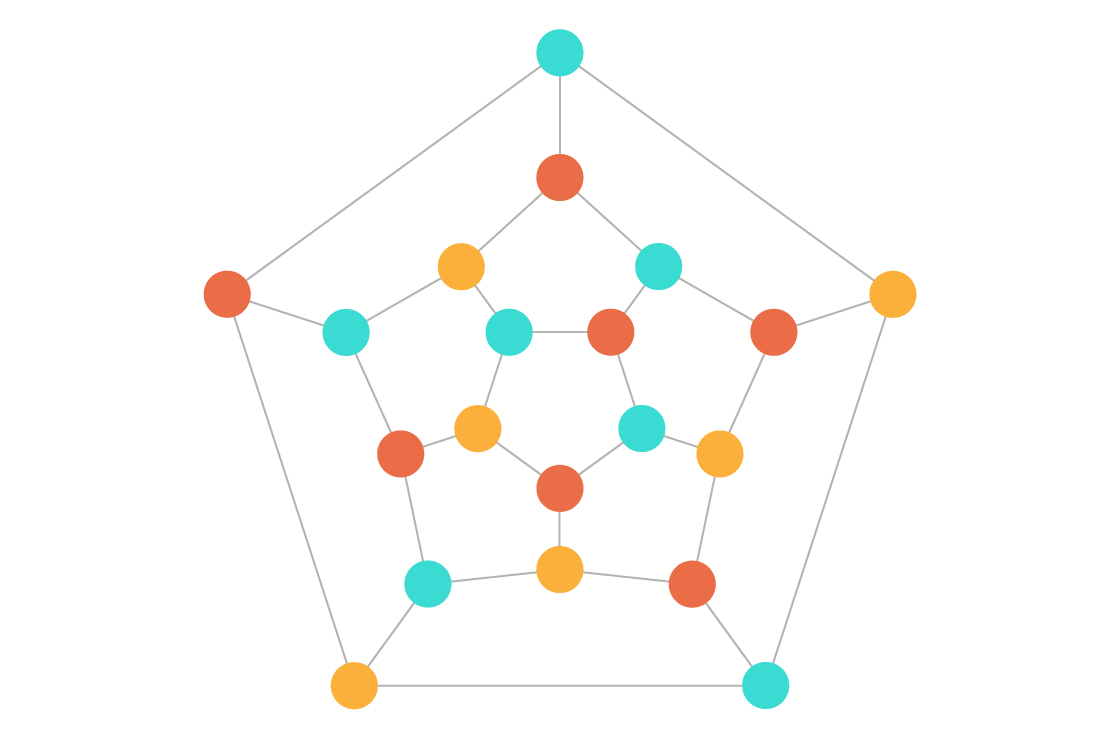
In a three-colored graph, every vertex is one of three colors, and no connected vertexes share the same color.
5W Infographics for Quanta Magazine
This “three-color” problem is hard to solve. In general, the time it takes to find a three-coloring of a graph (or determine that none exists) increases exponentially as the size of the graph increases. If, say, finding a solution for a graph with 20 vertices takes 320 nanoseconds — a few seconds total — a graph with 60 vertices would take on the order of 360 nanoseconds, or about 100 times the age of the universe.
But let’s say someone claims to have three-colored a graph. It wouldn’t take long to check whether their claim is true. You’d just go through the vertices one by one, examining their connections. As the graph gets bigger, the time it takes to do this increases slowly, in what’s called polynomial time. As a result, a computer doesn’t take much longer to check a three-coloring of a graph with 60 vertices than it does to check a graph with 20 vertices.
“It’s easy, given a proper three-coloring, to check that it works,” said John Wright, a physicist at the Massachusetts Institute of Technology who wrote the new paper along with Anand Natarajan of Caltech.
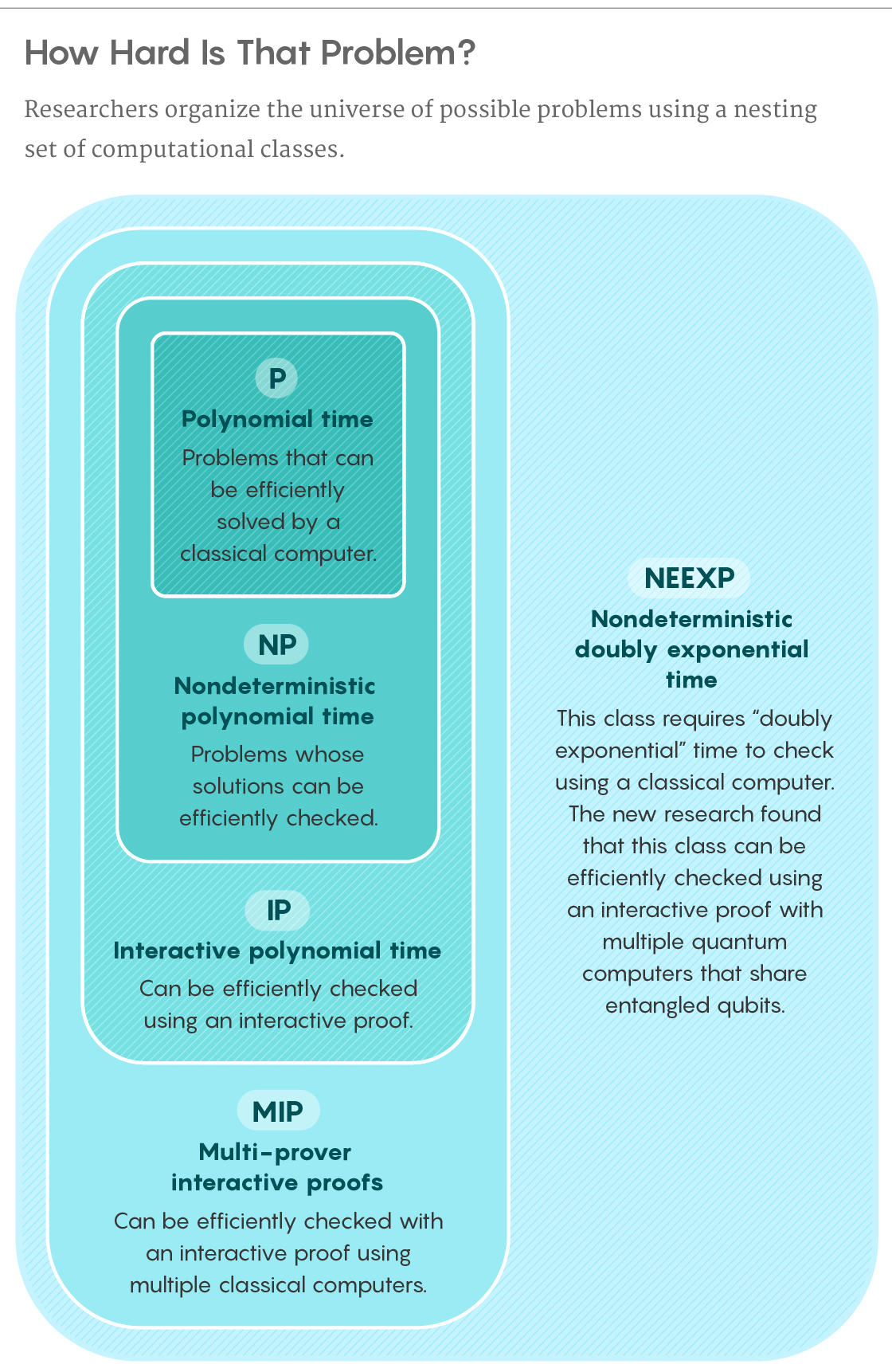
In the 1970s computer scientists defined a class of problems that are easy to verify, even if some are hard to solve. They called the class “NP,” for nondeterministic polynomial time. Since then, NP has been the most intensively studied class of problems in computer science. In particular, computer scientists would like to know how this class changes as you give the verifier new ways to check the truth of a solution.
The Right Questions
Prior to Natarajan and Wright’s work, verification power had increased in two big leaps.
To understand the first leap, imagine that you’re colorblind. Someone places two blocks on the table in front of you and asks whether the blocks are the same or different colors. This is an impossible task for you. Moreover, you can’t verify someone else’s solution.
But you’re allowed to interrogate this person, whom we’ll call the prover. Let’s say the prover tells you that the two blocks are different colors. You designate one block as “Block A” and the other as “Block B.” Then you place the blocks behind your back and randomly switch which hand holds which block. Then you reveal the blocks and ask the prover to identify Block A.
If the blocks are different colors, this couldn’t be a simpler quiz. The prover will know that Block A is, say, the red block and will correctly identify it every single time.
But if the blocks are actually the same color — meaning the prover erred in saying that they were different colors — the prover can only guess which block is which. Because of this, it will only be possible for the prover to identify Block A 50 percent of the time. By repeatedly probing the prover about the solution, you will be able to verify whether it’s correct.

David Sella

Soya Park
Anand Natarajan (top) and John Wright exploited quantum mechanics in their new work.
Anand Natarajan (left) and John Wright exploited quantum mechanics in their new work.
David Sella (Natarajan); Soya Park (Wright)
“The verifier can send the prover questions,” Wright said, “and maybe at the end of the conversation the verifier can become more convinced.”
In 1985 a trio of computer scientists proved that such interactive proofs can be used to verify solutions to problems that are more complicated than the problems in NP. Their work created a new class of problems called IP, for “interactive polynomial” time. The same method used to verify the coloring of two blocks can be used to verify solutions to much more complicated questions.
The second major advance took place in the same decade. It follows the logic of a police investigation. If you have two suspects you believe committed a crime, you’re not going to question them together. Instead, you’ll interrogate them in separate rooms and check each person’s answers against the other’s. By questioning them separately, you’ll be able to reveal more of the truth than if you had only one suspect to interrogate.
“It’s impossible for [two suspects] to form some sort of distributed, consistent story because they simply don’t know what answers the other is giving,” Wright said.
In 1988 four computer scientists proved that if you ask two computers to separately solve the same problem — and you interrogate them separately about their answers — you can verify a class of problems that’s even larger than IP: a class called MIP, for multi-prover interactive proofs.
With a multi-prover interactive approach, for example, it’s possible to verify three-colorings for a sequence of graphs that increase in size much faster than the graphs in NP. In NP, graph sizes increase at a linear rate — the number of vertices might grow from 1 to 2 to 3 to 4 and so on — so that the size of a graph is never hugely disproportionate to the amount of time needed to verify its three-coloring. But in MIP, the number of vertices in a graph grows exponentially — from 21 to 22 to 23 to 24 and so on.
As a result, the graphs are too big even to fit in the verifying computer’s memory, so it can’t check three-colorings by running through the list of vertices. But it’s still possible to verify a three-coloring by asking the two provers separate but related questions.
In MIP, the verifier has enough memory to run a program that allows it to determine whether two vertices in the graph are connected by an edge. The verifier can then ask each prover to state the color of one of the two connected vertices — and it can cross-reference the provers’ answers to make sure the three-coloring works.
The expansion of hard-to-solve-but-easy-to-verify problems from NP to IP to MIP involved classical computers. Quantum computers work very differently. For decades it’s been unclear how they change the picture — do they make it harder or easier to verify solutions?
The new work by Natarajan and Wright provides the answer.
Quantum Cheats
Quantum computers perform calculations by manipulating quantum bits, or “qubits.” These have the strange property that they can be entangled with one another. When two qubits — or even large systems of qubits — are entangled, it means that their physical properties play off each other in a certain way.
In their new work, Natarajan and Wright consider a scenario involving two separate quantum computers that share entangled qubits.
This kind of setup would seem to work against verification. The power of a multi-prover interactive proof comes precisely from the fact that you can question two provers separately and cross-check their answers. If the provers’ answers are consistent, then it’s likely they’re correct. But two provers sharing an entangled state would seem to have more power to consistently assert incorrect answers.
And indeed, when the scenario of two entangled quantum computers was first put forward in 2003, computer scientists assumed entanglement would reduce verification power. “The obvious reaction of everyone, including me, is that now you’re giving more power to the provers,” Vidick said. “They can use entanglement to correlate their answers.”
Despite that initial pessimism, Vidick spent several years trying to prove the opposite. In 2012, he and Tsuyoshi Ito proved that it’s still possible to verify all the problems in MIP with entangled quantum computers.
Natarajan and Wright have now proved that the situation is even better than that: A wider class of problems can be verified with entanglement than without it. It’s possible to turn the connections between entangled quantum computers to the verifier’s advantage.
To see how, remember the procedure in MIP for verifying three-colorings of graphs whose sizes grow exponentially. The verifier doesn’t have enough memory to store the whole graph, but it does have enough memory to identify two connected vertices, and to ask the provers the colors of those vertices.
With the class of problems Natarajan and Wright consider — called NEEXP for nondeterministic doubly exponential time — the graph sizes grow even faster than they do in MIP. Graphs in NEEXP grow at a “doubly exponential” rate. Instead of increasing at a rate of powers of 2 — 21, 22, 23, 24 and so on — the number of vertices in the graph increases at a rate of powers of powers of 2 — $latex 2^{2^1}, 2^{2^2}, 2^{2^3}, 2^{2^4}$ and so on. As a result, the graphs quickly become so big that the verifier can’t even identify a single pair of connected vertices.
5W Infographics for Quanta Magazine
“To label a vertex would take 2n bits, which is exponentially more bits than the verifier has in its working memory,” Natarajan said.
But Natarajan and Wright prove that it’s possible to verify a three-coloring of a doubly-exponential-size graph even without being able to identify which vertices to ask the provers about. This is because you can make the provers come up with the questions themselves.
The idea of asking computers to interrogate their own solutions sounds, to computer scientists, as advisable as asking suspects in a crime to interrogate themselves — surely a foolish proposition. Except Natarajan and Wright prove that it’s not. The reason is entanglement.
“Entangled states are a shared resource,” Wright said. “Our entire protocol is figuring out how to use this shared resource to generate connected questions.”
If the quantum computers are entangled, then their choices of vertices will be correlated, producing just the right set of questions to verify a three-coloring.
At the same time, the verifier doesn’t want the two quantum computers to be so intertwined that their answers to those questions are correlated (which would be the equivalent of two suspects in a crime coordinating their false alibis). Another strange quantum feature handles this concern. In quantum mechanics, the uncertainty principle prevents us from knowing a particle’s position and momentum simultaneously — if you measure one property, you destroy information about the other. The uncertainty principle strictly limits what you can know about any two “complementary” properties of a quantum system.
Natarajan and Wright take advantage of this in their work. To compute the color of a vertex, they have the two quantum computers make complementary measurements. Each computer computes the color of its own vertex, and in doing so, it destroys any information about the other’s vertex. In other words, entanglement allows the computers to generate correlated questions, but the uncertainty principle prevents them from colluding when answering them.
“You have to force the provers to forget, and that’s the main thing [Natarajan and Wright] do in their paper,” Vidick said. “They force the prover to erase information by making a measurement.”
Their work has almost existential implications. Before this new paper, there was a much lower limit on the amount of knowledge we could possess with complete confidence. If we were presented with an answer to a problem in NEEXP, we’d have no choice but to take it on faith. But Natarajan and Wright have burst past that limit, making it possible to verify answers to a far more expansive universe of computational problems.
And now that they have, it’s unclear where the limit of verification power lies.
“It could go much further,” said Lance Fortnow, a computer scientist at the Georgia Institute of Technology. “They leave open the possibility that you could take another step.”





