The Simple Idea Behind Einstein’s Greatest Discoveries

Rachel Suggs for Quanta Magazine
Introduction
The flashier fruits of Albert Einstein’s century-old insights are by now deeply embedded in the popular imagination: Black holes, time warps and wormholes show up regularly as plot points in movies, books, TV shows. At the same time, they fuel cutting-edge research, helping physicists pose questions about the nature of space, time, even information itself.
Perhaps ironically, though, what is arguably the most revolutionary part of Einstein’s legacy rarely gets attention. It has none of the splash of gravitational waves, the pull of black holes or even the charm of quarks. But lurking just behind the curtain of all these exotic phenomena is a deceptively simple idea that pulls the levers, shows how the pieces fit together, and lights the path ahead.
The idea is this: Some changes don’t change anything. The most fundamental aspects of nature stay the same even as they seemingly shape-shift in unexpected ways. Einstein’s 1905 papers on relativity led to the unmistakable conclusion, for example, that the relationship between energy and mass is invariant, even though energy and mass themselves can take vastly different forms. Solar energy arrives on Earth and becomes mass in the form of green leaves, creating food we can eat and use as fuel for thought. (“What is this mind of ours: what are these atoms with consciousness?” asked the late Richard Feynman. “Last week’s potatoes!”) That’s the meaning of E = mc2. The “c” stands for the speed of light, a very large number, so it doesn’t take much matter to produce an enormous amount of energy; in fact, the sun turns millions of tons of mass into energy each second.
This endless morphing of matter into energy (and vice versa) powers the cosmos, matter, life. Yet through it all, the energy-matter content of the universe never changes. It’s strange but true: Matter and energy themselves are less fundamental than the underlying relationships between them.
We tend to think of things, not relationships, as the heart of reality. But most often, the opposite is true. “It’s not the stuff,” said the Brown University physicist Stephon Alexander.
The same is true, Einstein showed, for “stuff” like space and time, seemingly stable, unchangeable aspects of nature; in truth, it’s the relationship between space and time that always stays the same, even as space contracts and time dilates. Like energy and matter, space and time are mutable manifestations of deeper, unshakable foundations: the things that never vary no matter what.
“Einstein’s deep view was that space and time are basically built up by relationships between things happening,” said the physicist Robbert Dijkgraaf, director of the Institute for Advanced Study in Princeton, New Jersey, where Einstein spent his final decades.
The relationship that eventually mattered most to Einstein’s legacy was symmetry. Scientists often describe symmetries as changes that don’t really change anything, differences that don’t make a difference, variations that leave deep relationships invariant. Examples are easy to find in everyday life. You can rotate a snowflake by 60 degrees and it will look the same. You can switch places on a teeter-totter and not upset the balance. More complicated symmetries have led physicists to the discovery of everything from neutrinos to quarks — they even led to Einstein’s own discovery that gravitation is the curvature of space-time, which, we now know, can curl in on itself, pinching off into black holes.
Over the past several decades, some physicists have begun to question whether focusing on symmetry is still as productive as it used to be. New particles predicted by theories based on symmetries haven’t appeared in experiments as hoped, and the Higgs boson that was detected was far too light to fit into any known symmetrical scheme. Symmetry hasn’t yet helped to explain why gravity is so weak, why the vacuum energy is so small, or why dark matter remains transparent.
“There has been, in particle physics, this prejudice that symmetry is at the root of our description of nature,” said the physicist Justin Khoury of the University of Pennsylvania. “That idea has been extremely powerful. But who knows? Maybe we really have to give up on these beautiful and cherished principles that have worked so well. So it’s a very interesting time right now.”

Light
Einstein wasn’t thinking about invariance or symmetry when he wrote his first relativity papers in 1905, but historians speculate that his isolation from the physics community during his employment in the Swiss patent office might have helped him see past the unnecessary trappings people took for granted.
Like other physicists of his time, Einstein was pondering several seemingly unrelated puzzles. James Clerk Maxwell’s equations revealing the intimate connection between electric and magnetic fields looked very different in different frames of reference — whether an observer is moving or at rest. Moreover, the speed at which electromagnetic fields propagated through space almost precisely matched the speed of light repeatedly measured by experiments — a speed that didn’t change no matter what. An observer could be running toward the light or rushing away from it, and the speed didn’t vary.
Einstein connected the dots: The speed of light was a measurable manifestation of the symmetrical relationship between electric and magnetic fields — a more fundamental concept than space itself. Light didn’t need anything to travel through because it was itself electromagnetic fields in motion. The concept of “at rest” — the static “empty space” invented by Isaac Newton — was unnecessary and nonsensical. There was no universal “here” or “now”: Events could appear simultaneous to one observer but not another, and both perspectives would be correct.
Chasing after a light beam produced another curious effect, the subject of Einstein’s second relativity paper, “Does the Inertia of a Body Depend Upon Its Energy Content?” The answer was yes. The faster you chase, the harder it is to go faster. Resistance to change becomes infinite at the speed of light. Since that resistance is inertia, and inertia is a measure of mass, the energy of motion is transformed into mass. “There is no essential distinction between mass and energy,” Einstein wrote.
It took several years for Einstein to accept that space and time are inextricably interwoven threads of a single space-time fabric, impossible to disentangle. “He still wasn’t thinking in a fully unified space-time sort of way,” said David Kaiser, a physicist and historian of science at the Massachusetts Institute of Technology.
Unified space-time is a difficult concept to wrap our minds around. But it begins to make sense if we think about the true meaning of “speed.” The speed of light, like any speed, is a relationship — distance traveled over time. But the speed of light is special because it can’t change; your laser beam won’t advance any faster just because it is shot from a speeding satellite. Measurements of distance and time must therefore change instead, depending on one’s state of motion, leading to effects known as “space contraction” and “time dilation.” The invariant is this: No matter how fast two people are traveling with respect to each other, they always measure the same “space-time interval.” Sitting at your desk, you hurtle through time, hardly at all through space. A cosmic ray flies over vast distances at nearly the speed of light but traverses almost no time, remaining ever young. The relationships are invariant no matter how you switch things around.

Gravity
Einstein’s special theory of relativity, which came first, is “special” because it applies only to steady, unchanging motion through space-time — not accelerating motion like the movement of an object falling toward Earth. It bothered Einstein that his theory didn’t include gravity, and his struggle to incorporate it made symmetry central to his thinking. “By the time he gets full-on into general relativity, he’s much more invested in this notion of invariants and space-time intervals that should be the same for all observers,” Kaiser said.
Specifically, Einstein was puzzled by a difference that didn’t make a difference, a symmetry that didn’t make sense. It’s still astonishing to drop a wad of crumped paper and a set of heavy keys side by side to see that somehow, almost magically, they hit the ground simultaneously — as Galileo demonstrated (at least apocryphally) by dropping light and heavy balls off the tower in Pisa. If the force of gravity depends on mass, then the more massive an object is, the faster it should sensibly fall. Inexplicably, it does not.
The key insight came to Einstein in one of his famous thought experiments. He imagined a man falling off a building. The man would be floating as happily as an astronaut in space, until the ground got in his way. When Einstein realized that a person falling freely would feel weightless, he described the discovery as the happiest thought of his life. It took a while for him to pin down the mathematical details of general relativity, but the enigma of gravity was solved once he showed that gravity is the curvature of space-time itself, created by massive objects like the Earth. Nearby “falling” objects like Einstein’s imaginary man or Galileo’s balls simply follow the space-time path carved out for them.
When general relativity was first published, 10 years after the special version, a problem arose: It appeared that energy might not be conserved in strongly curved space-time. It was well-known that certain quantities in nature are always conserved: the amount of energy (including energy in the form of mass), the amount of electric charge, the amount of momentum. In a remarkable feat of mathematical alchemy, the German mathematician Emmy Noether proved that each of these conserved quantities is associated with a particular symmetry, a change that doesn’t change anything.
Noether showed that the symmetries of general relativity — its invariance under transformations between different reference frames — ensure that energy is always conserved. Einstein’s theory was saved. Noether and symmetry have both occupied center stage in physics ever since.
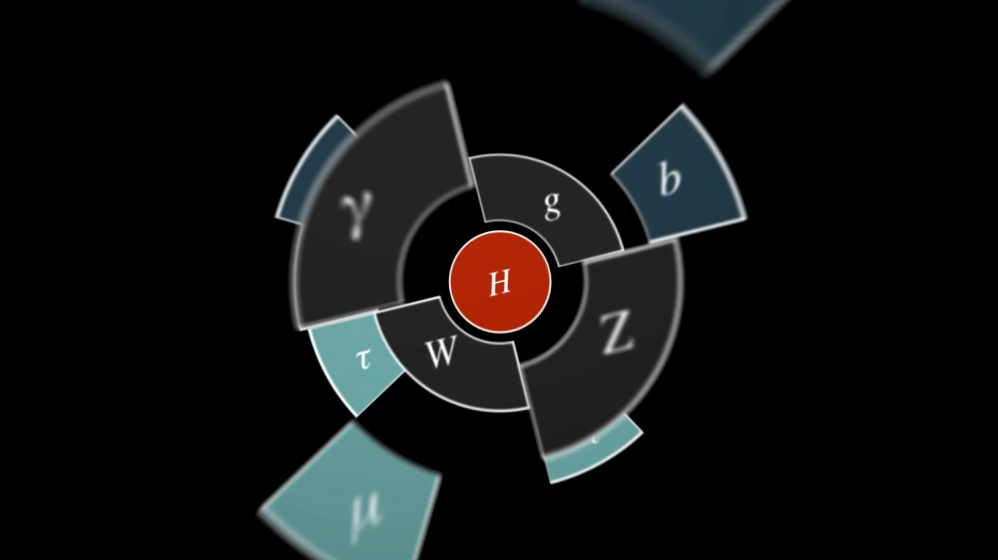
Matter
Post Einstein, the pull of symmetry only became more powerful. Paul Dirac, trying to make quantum mechanics compatible with the symmetry requirements of special relativity, found a minus sign in an equation suggesting that “antimatter” must exist to balance the books. It does. Soon after, Wolfgang Pauli, in an attempt to account for the energy that seemed to go missing during the disintegration of radioactive particles, speculated that perhaps the missing energy was carried away by some unknown, elusive particle. It was, and that particle is the neutrino.
Starting in the 1950s, invariances took on a life of their own, becoming ever more abstract, “leaping out,” as Kaiser put it, from the symmetries of space-time. These new symmetries, known as “gauge” invariances, became extremely productive, “furnishing the world,” Kaiser said, by requiring the existence of everything from W and Z bosons to gluons. “Because we think there’s a symmetry that’s so fundamental it has to be protected at all costs, we invent new stuff,” he said. Gauge symmetry “dictates what other ingredients you have to introduce.” It’s roughly the same kind of symmetry as the one that tells us that a triangle that’s invariant under 120-degree rotations must have three equal sides.
Gauge symmetries describe the internal structure of the system of particles that populates our world. They indicate all the ways physicists can shift, rotate, distort and generally mess with their equations without varying anything important. “The symmetry tells you how many ways you can flip things, change the way the forces work, and it doesn’t change anything,” Alexander said. The result is a peek at the hidden scaffolding that supports the basic ingredients of nature.
The abstractness of gauge symmetries causes a certain unease in some quarters. “You don’t see the whole apparatus, you only see the outcome,” Dijkgraaf said. “I think with gauge symmetries there’s still a lot of confusion.”
To compound the problem, gauge symmetries produce a multitude of ways to describe a single physical system — a redundancy, as the physicist Mark Trodden of the University of Pennsylvania put it. This property of gauge theories, Trodden explained, renders calculations “fiendishly complicated.” Pages and pages of calculations lead to very simple answers. “And that makes you wonder: Why? Where does all that complexity in the middle come from? And one possible answer to that is this redundancy of description that gauge symmetries give you.”
Such internal complexity is the opposite of what symmetry normally offers: simplicity. With a tiling pattern that repeats itself, “you only need to look at one little bit and you can predict the rest of it,” Dijkgraaf said. You don’t need one law for the conservation of energy and another for matter where only one will do. The universe is symmetrical in that it’s homogeneous on large scales; it doesn’t have a left or right, up or down. “If that weren’t the case, cosmology would be a big mess,” Khoury said.

Broken Symmetries
The biggest problem is that symmetry as it’s now understood seems to be failing to answer some of the biggest questions in physics. True, symmetry told physicists where to look for both the Higgs boson and gravitational waves — two momentous discoveries of the past decade. At the same time, symmetry-based reasoning predicted a slew of things that haven’t shown up in any experiments, including the “supersymmetric” particles that could have served as the cosmos’s missing dark matter and explained why gravity is so weak compared to electromagnetism and all the other forces.
In some cases, symmetries present in the underlying laws of nature appear to be broken in reality. For instance, when energy congeals into matter via the good old E = mc2, the result is equal amounts of matter and antimatter — a symmetry. But if the energy of the Big Bang created matter and antimatter in equal amounts, they should have annihilated each other, leaving not a trace of matter behind. Yet here we are.
The perfect symmetry that should have existed in the early hot moments of the universe somehow got destroyed as it cooled down, just as a perfectly symmetrical drop of water loses some of its symmetry when it freezes into ice. (A snowflake may look the same in six different orientations, but a melted snowflake looks the same in every direction.)
“Everyone’s interested in spontaneously broken symmetries,” Trodden said. “The law of nature obeys a symmetry, but the solution you’re interested in does not.”
But what broke the symmetry between matter and antimatter?
It would come as a surprise to no one if physics today turned out to be burdened with unnecessary scaffolding, much like the notion of “empty space” that misdirected people before Einstein. Today’s misdirection, some think, may even have to do with the obsession with symmetry itself, at least as it’s currently understood.
Many physicists have been exploring an idea closely related to symmetry called “duality.” Dualities are not new to physics. Wave-particle duality — the fact that the same quantum system is best described as either a wave or a particle, depending on the context — has been around since the beginning of quantum mechanics. But newfound dualities have revealed surprising relationships: For example, a three-dimensional world without gravity can be mathematically equivalent, or dual, to a four-dimensional world with gravity.
If descriptions of worlds with different numbers of spatial dimensions are equivalent, then “one dimension in some sense can be thought of as fungible,” Trodden said.
“These dualities include elements — the number of dimensions — we think about as invariant,” Dijkgraaf said, “but they are not.” The existence of two equivalent descriptions with all the attendant calculations raises “a very deep, almost philosophical point: Is there an invariant way to describe physical reality?”
No one is giving up on symmetry anytime soon, in part because it’s proved so powerful and also because relinquishing it means, to many physicists, giving up on “naturalness” — the idea that the universe has to be exactly the way it is for a reason, the furniture arranged so impeccably that you couldn’t imagine it any other way.
Clearly, some aspects of nature — like the orbits of the planets — are the result of history and accident, not symmetry. Biological evolution is a combination of known mechanisms and chance. Perhaps Max Born was right when he responded to Einstein’s persistent objection that “God does not play dice” by pointing out that “nature, as well as human affairs, seems to be subject to both necessity and accident.”
Certain aspects of physics will have to remain intact — causality for example. “Effects cannot precede causes,” Alexander said. Other things almost certainly will not.
One aspect that will surely not play a key role in the future is the speed of light, which grounded Einstein’s work. The smooth fabric of space-time Einstein wove a century ago inevitably gets ripped to shreds inside black holes and at the moment of the Big Bang. “The speed of light can’t remain constant if space-time is crumbling,” Alexander said. “If space-time is crumbling, what is invariant?”
Certain dualities suggest that space-time emerges from something more basic still, the strangest relationship of all: What Einstein called the “spooky” connections between entangled quantum particles. Many researchers believe these long-distance links stitch space-time together. As Kaiser put it, “The hope is that something like a continuum of space-time would emerge as a secondary effect of more fundamental relationships, including entanglement relationships.” In that case, he said, classical, continuous space-time would be an “illusion.”
The high bar for new ideas is that they cannot contradict consistently reliable theories like quantum mechanics and relativity — including the symmetries that support them.
Einstein once compared building a new theory to climbing a mountain. From a higher perspective, you can see the old theory still standing, but it’s altered, and you can see where it fits into the larger, more inclusive landscape. Instead of thinking, as Feynman suggested, with last week’s potatoes, future thinkers might ponder physics using the information encoded in quantum entanglements, which weave the space-time to grow potatoes in the first place.
This article was reprinted on Wired.com.