Inside the Knotty World of ‘Anyon’ Particles
James O’Brien for Quanta Magazine
Introduction
Prior to the emergence of quantum mechanics, fundamental physics was marked by a peculiar dualism. On the one hand, we had electric and magnetic fields, governed by Maxwell’s equations. The fields filled all of space and were continuous. On the other hand, we had atoms, governed by Newtonian mechanics. The atoms were spatially limited — indeed, quite small — discrete objects. At the heart of this dualism was the contrast of light and substance, a theme that has fascinated not only scientists but artists and mystics for many centuries.
One of the glories of quantum theory is that it has replaced that dualistic view of matter with a unified one. We learned to make fields from photons, and atoms from electrons (together with other elementary particles). Both photons and electrons are described using the same mathematical structure. They are particles, in the sense that they come in discrete units with definite, reproducible properties. But the new quantum-mechanical sort of “particle” cannot be associated with a definite location in space. Instead, the possible results of measuring its position are given by a probability distribution. And that distribution is given as the square of a space-filling field, its so-called wave function.
Conceptually, quantum particles differ so significantly from their classical ancestors that a different name seems in order. Just as the quantum “qubit” was named by analogy to the classical “bit” of information, I will use the term “quarticle” (pronounced kwort-icle) for a quantum particle. This emphasis on the particle aspect (as opposed to “wavicle”) is appropriate, because in practice quantum physicists usually analyze quantum behavior by visualizing the behavior of particles, and then refining — and, if necessary, correcting — their picture until it works for quarticles.
II.
The quantum unification of light and substance, while satisfying, is limited in scope. For when we go beyond single quarticles to consider the behavior of collections of identical quarticles, a new dualism appears. Indeed, the world of quantum particles divides into two great, mutually exclusive kingdoms. There is the kingdom of bosons, named after Satyendra Bose, and the kingdom of fermions, named after Enrico Fermi. Every species of quarticle is either a boson or fermion.
Interactions among bosons are very different from those of fermions. We call this effect “quantum statistics.” For purposes of orientation, a simple introduction may be in order.
Bosons are conformists. They like to behave in the same way. (More technically: Identical bosons have enhanced probability to occupy the same quantum state.) Photons belong to the kingdom of bosons. A laser beam is the epitome of boson-ness. It consists of many photons of the same wavelength (that is, color) moving in the same direction, the result of “stimulated emission” of photons in an imitative cascade.
Fermions, by contrast, are individualists. They absolutely refuse to occupy the same quantum state, a fact known as the Pauli exclusion principle. Electrons belong to the kingdom of fermions, and this is a key reason why the periodic table exists. Electrons, being negatively charged, are strongly attracted to positively charged atomic nuclei, but they prevent one another from surrounding the nucleus in a simple, efficient way. Instead they build up complex configurations that can support interesting chemistry.
Supersymmetry is a theoretical speculation that — if true — would reconcile the two kingdoms. According to supersymmetry, every elementary quarticle has a mate in the opposite kingdom, its superpartner. The superpartner of a boson is a fermion, and vice versa. Superpartners share the same electric charge and several other properties, but differ in mass and spin.
Supersymmetry is an attractive, logical extension of known physics, and it can be implemented with elegant mathematics. Many physicists, including me, feel that it deserves to be true.
But the last word, naturally, goes to nature. While there is compelling circumstantial evidence for supersymmetry, as yet there is no direct proof. For that, we need to find some superpartners. Searching for superpartners of known particles is a major preoccupation of experimentalists working at the Large Hadron Collider. Sadly, the results so far are negative. Yet there is still considerable potential for discovery, as the machine comes to operate at higher energy and more collisions get analyzed.
III.
Clearly, quantum statistics lies at the foundation of our understanding of nature. Also, as we’ve seen, it raises a profound question about the unity of matter. Addressing that question suggests new possibilities for discovery.
Such an important concept deserves a worthy grounding. What is quantum statistics, at bottom?
The modern answer to that question is deep, beautiful and surprisingly recent. It emerged in the late 1970s, more than 50 years after quantum mechanics matured, and it was catalyzed by the pioneering work of Jon Leinaas and Jan Myrheim.
In brief, quantum statistics reflects the topology of quarticle world lines. In the next three paragraphs, I’ll unpack that dense bit of poetry.
In quantum theory, the probability for a process is expressed as the square of the amplitude of its wave function. Amplitudes are more basic and obey simpler rules than the probabilities they control. The central problem of quantum dynamics, therefore, is to calculate the wave-function amplitude for a given configuration of particles at an initial time to evolve into another configuration at a later time.
In calculating the total amplitude for two indistinguishable quarticles that begin at positions A and B and end at positions C and D, we must take into account contributions from every possible motion connecting the starting positions to the end points. These paths are the “world lines” of the quarticles. The motions divide into two classes: one class in which the two quarticles, which began at A and B, respectively, wind up at C and D, and another class in which they wind up at D and C.
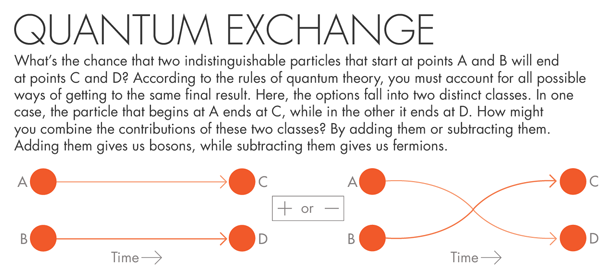
We need a rule for how to combine the contributions from those two classes. There are two mathematically consistent possibilities. We can add them, or we can subtract them. The “add” option gives us bosons, while the “subtract” option gives us fermions. All the characteristic properties of bosons and fermions can be deduced from those basic rules.
It is a wonderful intellectual achievement, to have traced such profoundly consequential properties of matter to a basic aspect of identity — that is, indistinguishability — and the topology of motion in space-time.
IV.
But the real payoff comes when we bring that basic understanding to bear on new situations and make new discoveries. The most dramatic application of our deeper understanding of quantum statistics arises when we consider quarticles that live in two dimensions, as I’ll now explain.
Perhaps surprisingly, in a world of two dimensions the topology of pairs (or larger groups) of world lines becomes much richer than in worlds of three or more. The reason is closely connected to a basic feature of knots.
In three space dimensions, knot theory is a subtle, complicated subject. But in four space dimensions it is trivial: All knots can be unraveled completely.
A knot, to mathematicians, is just a continuous curve in space. Imagine labeling each point on that tangled curve with the numbers between zero and one, with zero and one representing the same point. Now take a circle and do the same.
To untangle the knot, simply let the points on our knot flow to the points on the circle that are labeled with the corresponding number. Of course, obstructions to this unraveling might arise, such as when different parts of the curve come to intersect. But in four dimensions, we can always move two strands past one another.
The procedure is difficult to visualize directly, but we can understand it using a simple trick. Let us represent position in the extra dimension by the value of a fictitious temperature. If our threatened intersection occurs at a point where the temperatures of the strands are different, it is not a genuine intersection, because the strands are located differently in the extra dimension. And if the temperatures are the same, we need only make a temporary excursion into the extra dimension — heat one strand up, move it “through” (in the ordinary dimensions), and then cool it back down — to avoid the intersection.
The world lines of quarticles that move in three-dimensional space form strands in four-dimensional space-time. Therefore, as we’ve just seen, they can’t really get tangled up. Their topology reduces to keeping track of exchanges, as we discussed earlier.

With that richer topology comes much greater variety in the possibilities for adding up the contributions of world lines. In other words, there are many more possibilities for quantum statistics, and thus more categories of particles beyond bosons and fermions. I coined the word “anyon” to describe quarticles whose motion is restricted to two space dimensions, and which are neither bosons nor fermions. I meant this humorously, to suggest “anything goes,” but of course that implication should not be taken literally. Anyons must obey highly structured mathematical rules. Still, we find infinitely many consistent possibilities for them, instead of only two.
Because the rules for anyon behavior are sensitive to the quarticles’ motion over time, anyons have memory. More precisely: Since the amplitude for an evolution involving anyons will be different, depending on how their world lines got tangled up over time, the value of the amplitude provides a record of their relative motion. As we’ll discuss momentarily, the memory abilities of anyons might power an important technology.
V.
Do anyons exist, outside of theorists’ imaginations?
Our immediate reaction might be: “Not in our world, since space is (at least) three-dimensional.” But that conclusion fails to reckon with nature’s creativity, and ours.
Two-dimensional universes, in fact, are all around us. We call them surfaces, films, membranes or interfaces. They can be accessed from “our” enveloping three-dimensional world, but they also have a life of their own. In more prosaic terms, some of those two-dimensional objects trap energy efficiently, and if they are not disturbed, their behavior will be self-contained.
The properties of these universes depend, of course, on what they’re made from, and on the pattern of their construction. Recently, there has been much interest in two-dimensional materials whose electrons are “highly entangled.” The precise, technical definition of that phrase involves deep concepts in the mathematics of quantum theory. Here a rough analogy will have to serve.
When electrons form covalent bonds, they cannot move independently; they are, we may say, frozen in place, forming a kind of solid. Quantum fluctuations may cause that solid to sublime, producing materials in which the electrons move freely — a kind of electron gas. This is a crude but extremely useful way to describe the electrons in metals. But we can also imagine intermediate cases, where the electrons are neither locked in place nor independent, forming a sort of liquid.
These strange liquids, which melted due to quantum fluctuations rather than thermal agitation, are especially interesting. In this state, the electrons remain orderly, yet they are not rigidly stifled. Their order involves subtle quantum correlations — that is, entanglement.
Imperfections in these liquids’ orderly arrangement behave much like impurities in ordinary liquids. They form stable arrangements that retain their basic structure, even as they move. Thus, they are a kind of emergent particle — or rather, since we’re concerned with quantum liquids, a kind of emergent quarticle. These emergent quarticles are several steps removed from individual electrons, and they can have quite different properties from those of electrons.
“Everything not forbidden is compulsory.” That memorable phrase, from T.H. White’s novel The Once and Future King, expresses an important principle of quantum behavior: The spontaneous activity of quantum systems explores all consistent possibilities. For me, it has also been an inspiring principle for theoretical exploration: Nature, in her abundance, provides materials to embody all theoretically consistent possibilities. Trusting in that principle, I strive to exercise what Richard Feynman called “imagination in a straitjacket,” expecting that
If you build it (imaginatively), they will come (physically).
So it has proved for anyons. Physicists now know of several two-dimensional quantum liquids whose emergent quarticles are neither bosons nor fermions, but rather different sorts of anyons.
The first example turned up in a fascinating domain of physics known as the fractional quantum Hall effect (FQHE). This is a state of matter that arises when electrons confined to a two-dimensional layer (typically, at the interface of two semiconductors) are taken to extremely low temperatures and subjected to extremely large magnetic fields. Under these conditions, as the density and magnetic field are varied, the electrons form a large class of related but distinct quantum liquids with remarkable properties.
Specifically, the emergent quarticles in those liquids typically carry electric charge that is a fraction of an electron’s charge, and they obey quantum statistics that is a fraction of fermion statistics. In the most robust FQHE state, for example, quarticles carry one-third of an electron’s electric charge. In general, the quarticles behave like one-third of an electron; indeed, an injected electron will fission into three of these quarticles. Consistent with that picture, the quarticles are predicted to be anyons, which exhibit one-third of fermion statistics. In mathematical terms, the amplitude for exchange of our quarticles will be multiplied by the cube root of –1.
The theory of the FQHE is highly developed and makes many successful predictions about the observed quantum liquids. Since anyonic quarticles are a central feature of that theory, there is little doubt among theorists that anyons exist in nature and are lurking in observed FQHE liquids. Numerical studies support that belief as well. Unfortunately, however, direct experimental proof has been difficult to come by, for a variety of practical reasons. Experimentalists continue to work on the problem, and they’re tantalizingly close to success.
Very recently a new class of quantum liquids, called spin liquids, has been identified. In these materials the electrons don’t move, but their spins — that is, the orientations of their spin axes — are in play. Spin liquids lie between ordinary magnets (spin solids), in which the directions of spins are rigidly aligned, and paramagnets and diamagnets (spin gases), in which the spin orientations are almost completely independent of one another. Theoretical models of two-dimensional spin liquids show that many of them support anyonic quarticles. The practical problems that plague FQHE studies of anyon behavior are less severe in spin liquids, so we can anticipate rapid progress.
Last but certainly not least, there has been considerable ferment in the engineering of artificial anyon systems. Recall that a basic feature of anyons, which distinguishes them from more familiar quarticles, is their memory. Many-anyon systems build up a gigantic collective memory, which can serve as a platform for computing. This so-called “topological quantum computing” is one plausible path toward building useful quantum computers. Microsoft is making major investments in this kind of research.
Topological quantum computing deserves extensive discussion, and I plan to return to it in a future column. Let me conclude this one with two pictures that point to the past and the future of that endeavor.
Computing with anyons exploits their ability to map their knotted histories into (observable) quantum-mechanical amplitudes. We move anyons around in clever ways and then access the tangled history of their motion. Topological quantum computing is, therefore, a form of computing with knots. As such, it is a modernization of quipu, the Incan technology for computation and encryption.
If topological computing does eventually lead to powerful quantum computers, then the most capable artificial intelligence will live in two-dimensional materials, embodied in circulating systems of anyons. We can look forward to a day when those super-brains reach out to thank their progenitors.



