How Our Universe Could Emerge as a Hologram
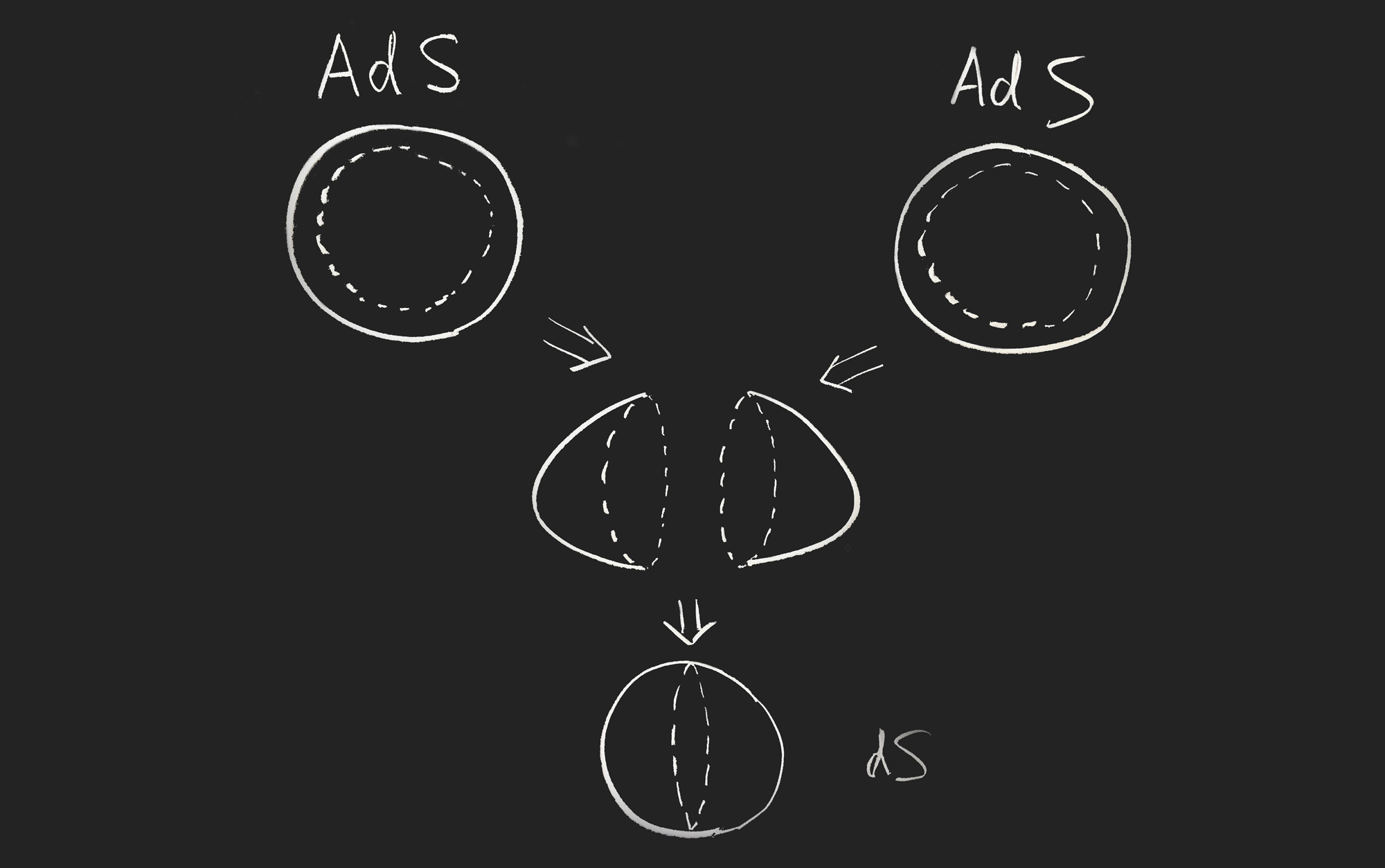
A sketch by Xi Dong of the cutting, warping and gluing procedure that he and his colleagues used to construct a hologram of a de Sitter universe.
Drawing by Xi Dong
Introduction
The fabric of space and time is widely believed by physicists to be emergent, stitched out of quantum threads according to an unknown pattern. And for 22 years, they’ve had a toy model of how emergent space-time can work: a theoretical “universe in a bottle,” as its discoverer, Juan Maldacena, has described it.
The space-time filling the region inside the bottle — a continuum that bends and undulates, producing the force called gravity — exactly maps to a network of quantum particles living on the bottle’s rigid, gravity-free surface. The interior “universe” projects from the lower-dimensional boundary system like a hologram. Maldacena’s discovery of this hologram has given physicists a working example of a quantum theory of gravity.
But that doesn’t necessarily mean the toy universe shows how space-time and gravity emerge in our universe. The bottle’s interior is a dynamic, Escheresque place called anti–de Sitter (AdS) space that is negatively curved like a saddle. Different directions on the saddle curve in opposite ways, with one direction curving up and the other curving down. The curves tend toward vertical as you move away from the center, ultimately giving AdS space its outer boundary — a surface where quantum particles can interact to create the holographic universe inside. However, in reality, we inhabit a positively curved “de Sitter (dS) space,” which resembles the surface of a sphere that’s expanding without bounds.
Ever since 1997, when Maldacena discovered the AdS/CFT correspondence — a duality between AdS space and a “conformal field theory” describing quantum interactions on that space’s boundary — physicists have sought an analogous description of space-time regions like ours that aren’t bottled up. The only “boundary” of our universe is the infinite future. But the conceptual difficulty of projecting a hologram from quantum particles living in the infinite future has long stymied efforts to describe real space-time holographically.
In the last year, though, three physicists have made progress toward a hologram of de Sitter space. Like the AdS/CFT correspondence, theirs is also a toy model, but some of the principles of its construction may extend to more realistic space-time holograms. There is “tantalizing evidence,” said Xi Dong of the University of California, Santa Barbara, who led the research, that the new model is a piece of “a unified framework for quantum gravity in de Sitter [space].”
Dong and co-authors Eva Silverstein of Stanford University and Gonzalo Torroba of the Bariloche Atomic Center in Argentina constructed a hologram of dS space by taking two AdS universes, cutting them, warping them and gluing their boundaries together.
The cutting is needed to deal with a problematic infinity: the fact that the boundary of AdS space is infinitely far away from its center. (Picture a ray of light traveling an infinite distance up the saddle’s curve to reach the edge.) Dong and co-authors rendered AdS space finite by chopping off the space-time region at a large radius. This created what’s known as a “Randall-Sundrum throat,” after the physicists Lisa Randall and Raman Sundrum, who devised the trick. This space is still approximated by a CFT that lives on its boundary, but the boundary is now a finite distance away.
Next, Dong and co-authors added ingredients from string theory to two of these theoretical Randall-Sundrum throats to energize them and give them positive curvature. This procedure, called “uplifting,” turned the two saddle-shaped AdS spaces into bowl-shaped dS spaces. The physicists could then do the obvious thing: “glue” the two bowls together along their rims. The CFTs describing both hemispheres become coupled with each other, forming a single quantum system that is holographically dual to the entire spherical de Sitter space.
“The resulting space-time has no boundary, but by construction it is dual to two CFTs,” Dong said. Because the equator of the de Sitter space, where the two CFTs live, is itself a de Sitter space, the construction is called the “dS/dS correspondence.”
Silverstein proposed this basic idea with three co-authors back in 2004, but new theoretical tools have enabled her, Dong and Torroba to study the dS/dS hologram in greater detail and show that it passes important consistency checks. In a paper published last summer, they calculated that the entanglement entropy — a measure of how much information is stored in the coupled CFTs living on the equator — matches the known entropy formula for the corresponding spherical region of de Sitter space.
They and other researchers are further exploring the de Sitter hologram using tools from computer science. As I described in a recent Quanta article, physicists have discovered in the last few years that the AdS/CFT correspondence works exactly like a “quantum error-correcting code” — a scheme for securely encoding information in a jittery quantum system, be it a quantum computer or a CFT. Quantum error correction may be how the emergent fabric of space-time achieves its robustness, despite being woven out of fragile quantum particles.
Dong, who was part of the team that discovered the connection between AdS/CFT and quantum error correction, said, “I believe that de Sitter holography also works as a quantum error-correcting code, and I would very much like to understand how.” There’s little hope of experimental evidence verifying that this new perspective on de Sitter space-time is correct, but according to Dong, “you instinctively know you are on the right track if the pieces start to fit together.”
Patrick Hayden, a theoretical physicist and computer scientist at Stanford who studies the AdS/CFT correspondence and its relationship to quantum error correction, said he and other experts are mulling over Dong, Silverstein and Torroba’s dS/dS model. He said it’s too soon to tell whether insights about how space-time is woven and how quantum gravity works in AdS space will carry over to a de Sitter model. “But there’s a path — something to be done,” Hayden said. “You can formulate concrete mathematical questions. I think a lot is going to happen in the next few years.”
This article was reprinted on Wired.com.




