Solution: ‘Is It Turtles All the Way Down?’

James Round for Quanta Magazine
Introduction
In February’s puzzle column, we explored some ways in which science can illuminate the knotty problem of infinite regress in biology and physics. As usual, Quanta readers engaged in a smart and lively discussion. Let’s first take a look at our questions and answers.
Question 1
Take a look at the change in facial features between our apelike ancestors and modern humans in this video rendition by the “paleoartist” John Gurche, in which 7 million years of evolutionary history are compressed into less than three minutes. At what point in the video would it no longer surprise you to see the depicted face in a gathering of humans in a modern city? Assuming that the video has a linear timescale, how long ago would that be?
First of all, kudos to the artist for producing this transition in such a striking way. For me, the face started looking vaguely human about halfway through (at around 1:20), although the brow ridges are still much too prominent and the nostrils and mouth far too wide. As Ty Rex comments, the face becomes more assuredly human around the mid 1:50s, which translates to about a million years ago assuming that the timescale in the video is linear (admittedly, a big assumption!). A million years ago was the era of Homo erectus, the hominid associated with increased sophistication of stone tools such as the hand axe. Cranial capacity was still somewhat below that of modern humans at this point, but it definitely entered the human range about half a million years ago with Homo heidelbergensis and the Neanderthals (starting 400,000 years ago). On Nova Science Now, David Pogue did an entertaining take on this question, roaming the streets of San Francisco with elaborate makeup designed to make him look like a Neanderthal. Of course, Neanderthals probably had more extreme cranial features than our direct ancestors.
Question 2
Our second question has to do with the apparent paradox: Which came first, the chicken or the egg? As I mentioned in the puzzle column, the problem only seems intractable because of the false implication that chickens were always chickens and eggs were always eggs. Below are my answers, for the four ways that I chose to define chickens and eggs.
1. Define “chicken” as the bird we would recognize today, and “egg” as the specific kind that would give rise to that bird. Which came first and how long ago?
Based on genetic studies, the chicken is thought to have been domesticated from a descendant of three or four species of jungle fowl (Gallus) from Southeast and South Asia. These birds can definitely pass for chickens to nonexpert eyes, and they evolved about 50 million years ago. Incidentally, these birds, and therefore chickens, are said to be the closest extant relatives of the theropod dinosaurs (including T. rex). The question of when a particular species actually originates within a lineage is very difficult to answer: The initial event is often a modest change that can only be appreciated in hindsight. In the case of the chicken, it might have been a mutation or perhaps a fertile cross of two existing species. In either case we would not consider the parent birds to be chickens. However, the egg that gives rise to the offspring would definitely be considered a chicken egg. So the short answer to the famous question is: It was the egg! For an entertaining discussion of the fight between Team Chicken and Team Egg, check out the short video here.
2. Define “chicken” as the bird we would recognize today, and “egg” as something similar in size and shape to one we would use in an omelet. Which came first and how long ago?
Eggs with rigid shells originated 150 million to 190 million years ago, long before chickens. The eggs came from some dinosaurs and early birds. So once again the winner is: the egg!
3. At some point in the evolutionary process, something emerged in the history of life called the alternation of generations. Organisms started existing in two alternating forms: One was the complex metabolizing organism (an animal or plant), and the second was a dormant entity such as an egg, seed or spore that would give rise to it. Define “chicken” as the first type and “egg” as the second type. Which came first and how long ago?
Seeds in plants and eggs in animals originated in the Devonian Period about 400 million years ago, when moving to land required that developing embryos have a concentrated food source within a durable waterproof shell. In this case, the ancestral organisms preceded the development of seeds and eggs, so this round goes to “chicken.”
4. When life first emerged, even the simplest forms had two components that coexisted — the biochemistry or set of chemical reactions it needed to metabolize and live, and the DNA or RNA or other code that could generate the organism from scratch, given the proper environment. Define “chicken” as the first part and “egg” as the second part. Which came first and how long ago?
One of the first scientific theories of the origin of life, proposed in the 1920s by the biochemist Alexander Oparin, held that life came from the chemical evolution of carbon-based molecules in Earth’s primordial soup. But James Watson and Francis Crick’s 1953 discovery (using crystallographic evidence from Rosalind Franklin) of the double-helix structure of DNA, so elegantly suited for replication, changed the consensus. While bombardment of organic molecules by primordial atmospheric conditions can give rise to complex biochemically important compounds, a replicator molecule like DNA or RNA is generally considered a sine qua non for the origin of life. Note that RNA can both replicate and catalyze some biochemical reactions, and thus could be the molecule that originally bridged the two functions. Recent studies seem to support the replicator model, which is required for molecular evolution to commence. That happened about 4 billion years ago, quite soon after the Earth formed and cooled.
So while we may never know the exact answer to this question, we have to award this round, on points, to the egg.
So the final score is: Egg: 3, Chicken: 1.
Puzzle 1
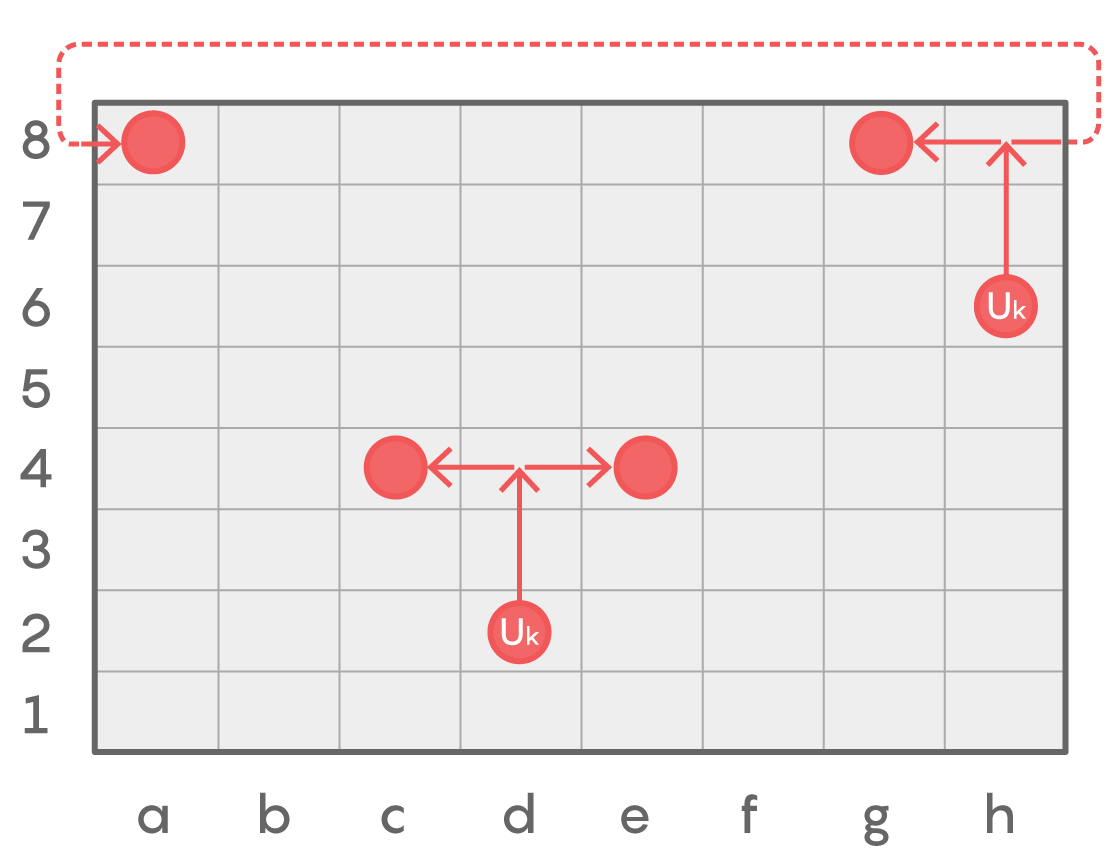
Imagine a two-dimensional universe divided into an 8-by-8 grid as shown below. This universe has a particle called a Uk (short for “upward knight”). The Uk can make a quantum jump to a square two squares above and one square to the left or right. Thus a Uk at d2 can move to c4 (up-left jump) or e4 (up-right jump), but not to any other square on this jump. If the Uk is in a position like h6, such that its up-right quantum jump will take it outside the universe’s grid, the particle will leave the universe on the right side and reappear via a wormhole on the left side at a8 in the position that it would have reached in the hypothetical grid of the adjacent parallel universe. From a8, an up-right jump takes it to b2, while an up-left jump will take it to h2, after a double wormhole ride. Two Uks that can reach the same square are said to be the same color. Based on the symmetry properties of the Uk’s jumps, how many colors does this universe have?
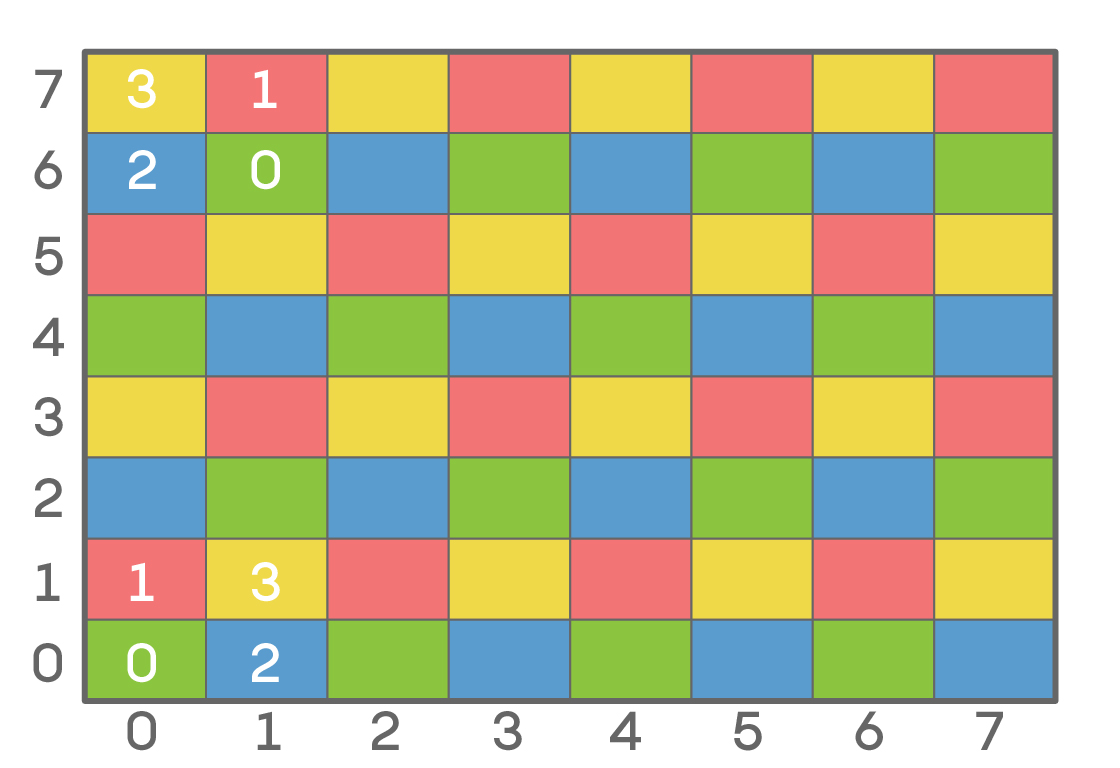
The answer is four, as shown by Michael Hickey, cornflower and Ty Rex. You can visualize the solution on the colored grid shown. A particle starting on a square of any color can only access the 16 squares of that particular color. What’s more, the particle can access all 16 squares of that color. Ty Rex came up with a simple and clever formula to describe the Uk’s moves. If we label the rows and columns as shown from 0 through 7, then every square has a color value from 0 through 3 given by the formula (2c + r) modulo 4, where c and r are the column and row numbers respectively. This is reflected in the colors: 0 is green, 1 is red, 2 is blue and 3 is yellow. Thus, for the blue square near the bottom left at column 1, row 0, the color value is (2 × 1 + 0) mod 4 = 2. For the blue square near the top left (column 0, row 6), the value is (2 × 0 + 6) mod 4, which is also 2. Every quantum leap keeps the color value constant, because c changes by +1 or −1 and r changes by +2. Thus a single jump adds either 2 × 1 + 2 = 4 or 2 × −1 + 2 = 0 to the original color value, which in both cases, mod 4, is 0. Thus, the particle always stays on a square of the same color. You can also verify that no matter which square you start on, you can reach every other square of the same color.
Puzzle 2
One of the first simple methods of generating pseudo-random numbers, the middle square method, was invented by the mathematician John von Neumann in 1949. You take a numeric seed with an even number of digits (say four), square it, and extract the middle four digits, which become the next seed. For example, if 7,478 is the seed, squaring it gives you 55,920,484, yielding the four digits 9,204, which become the next seed. If the square has fewer than eight digits, you add leading zeros.
The problem with this method is that if the middle four digits of the square are all zeros, the generator will then output only zeros. Also, the generator can get stuck in short repeating cycles for some other seed numbers. Can you tweak the middle square method by adding one or two additional rules that use simple substitution or arithmetic operations on one or more digits in order to increase the length of the longest cycle of four-digit numbers that the middle square method can generate, before a previous number is repeated?
Cornflower found that a simple tweak, which consists of simply adding the number 4888 to the middle square, yielded a cycle of length 341, which is far longer than the original method can generate. Cornflower graphed the results in a series of pretty pictures. (Thank you for that!)
The question of how to solve the problem of infinite regress in physics elicited comments about modern theories that avoid some of the more paradoxical aspects of cosmology such as singularities. Torbjörn Larsson highlighted the causality of relativity which “removes an absolute need for initial conditions,” leaving eternal processes like eternal inflation, which “put the bang in big bang” and drove the expansion of the universe. David Edwards favors the Einstein-Yang-Mills-Dirac-Higgs system, which has complete solutions without singularities and yields a cyclic universe, which is also an outcome favored by the theoretical physicist Roger Penrose using a different theory. You can check out their comments and responses for more details and links.
These theories do have the potential to enlarge our understanding of the beginning of the universe and its fate, but can they explain how the laws of the universe and universal constants and parameters took the form they did? It is clear that, unlike biology, physics has a long way to go to solve the problem of infinite regress. What’s required for this has been clearly stated by the cosmologist Lee Smolin. As Torbjörn commented, Smolin is considered a fringe figure in the field and has not had the compelling successes required for his theory of the evolution of the universe to become mainstream. However, in his book Time Reborn, Smolin uses philosophical principles to sketch out some of the qualities that an intellectually satisfactory and complete cosmological theory of the universe must have. I reproduce his criteria below (with some explanatory text in brackets):
• It should contain what we already know about nature, but as approximations.
• It should be scientific; that is, it has to make testable predictions for doable experiments [or experiments done by nature].
• It should solve the Why these laws?
• It should solve the initial-conditions problem.
• It should be causally and explanatorily closed. Nothing outside the universe should be required to explain anything inside the universe.
• It should satisfy the principle of sufficient reason, the principle of no unreciprocated action, and the principle of the identity of the indiscernibles. [Leibniz’s principle of sufficient reason states that there should be an answer to any reasonable question we might ask about why the universe has some particular feature. No unreciprocated action means that there should be nothing that affects the rest of the universe without being affected in return, which would rule out, for instance, Newtonian absolute time and absolute space. Identity of indiscernibles, another Leibniz principle, implies that two things that have the same relationships with everything else in the universe must actually be the same thing. This last principle precludes the existence of an infinite universe where every possible configuration and circumstance is repeated an infinite number of times: In that case, there would be no need to explain why something is the way it is!]
• Its physical variables should describe evolving relationships between dynamical entities. There should be no fixed-background structures, including fixed laws of nature. Hence the laws of nature evolve [based on changing dynamical conditions within the universe in time].
A pipe dream? Perhaps. But these ambitious principles must be met if we hope to carry bootstrapping to its ultimate limit and if we are to solve the problem of infinite regress to the same degree as has been done in biology. Until then, we will always have a frontier to explore and weave new theories about.
There were other interesting reader comments as well. Roger gave a compelling look at another pesky question: “Why is there something rather than nothing?” His answer is that when you remove all existing entities, then what remains “defines itself and is therefore the beginning point in the chain of being able to define existent entities in terms of other existent entities.” This idea, evocative of the “figure and ground” concept from Gestalt psychology, was also mentioned by Kyle Brown.
Robert Karl Stonjek tackled the infinite regress problem for consciousness. He states that “we subjectively see more than just the raw sensory input information but also see its interpretation and even our response to it. In other words conscious experience is at the point where input turns to output.” For instance, to see and recognize a face and make it seem familiar, we need “an extra layer of visual information not sourced [from] the visual input stream but add[ed] after non-conscious recognition processes have completed.” I agree completely. As the neuropsychologists Diane Rogers-Ramachandran and Vilayanur S. Ramachandran said in an article in 2008, “It is almost as though we are all hallucinating all the time and what we call object perception merely involves selecting the one hallucination that best matches the current sensory input, however fragmentary. Vision, in short, is controlled hallucination.” The Ramachandrans showed how this happens with everyday ambiguities and reaches its extreme in a particular neurological syndrome: “The extreme example of this effect is seen in patients who become completely blind and start hallucinating elves, circus animals and other objects — called the Charles Bonnet syndrome. In these individuals, only top-down inputs contribute to perception — the bottom-up processes, missing because they are blind (from macular degeneration or cataracts), can no longer limit their hallucinations.”
Interesting as this is, to address infinite regress for consciousness we need to answer the question: At what point in evolution does consciousness (internal experience) start, and with what experience? Do the desperate struggles of a badly crushed insect imply consciousness? It’s hard to imagine why not.
Just for fun, one last question to debate in the comments section below: Which came first, my puzzle questions or the ideas behind your answers?
The Quanta Insights prize goes to cornflower, who always makes stellar contributions and has just narrowly missed winning the prize previously. Thank you for your posts, cornflower — I’ve enjoyed and been impressed by every one of them.
And thank you to everyone who contributed to this great discussion. See you next month for more Insights!



