Solution: ‘A Drunkard’s Walk in Manhattan’
The Insights column for August explored the fascinating phenomenon of the drunkard’s walk, as it might take place in an idealized city with equal-size blocks. The drunkard’s walk, at the level of atoms and molecules, has long been known to underlie Brownian motion and the diffusion of fluids. Researchers have recently uncovered new insights into variants of the drunkard’s walk in a wider range of phenomena such as bacterial growth, snowflakes, mineral deposits and dendrites in caves, as reported by Kevin Hartnett in the Quanta article “A Unified Theory of Randomness.”
The city-block, or lattice, model of the drunkard’s walk is a simple yet interesting toy model that provides plenty of puzzles and insights. Let’s consider our two problems:
- Imagine that the drunkard is in the middle of a city laid out like a grid, with numbered streets running east to west and numbered avenues running north to south. The lamppost is at the corner of 5th Avenue and 5th Street, which we will designate as (5,5). The drunkard is sober enough to navigate a whole block before making a random choice at the next intersection. Let us say that after several such random block-length walks, he is now at (8,8). If we try to apply the circle argument shown above, we find that he can proceed to (9,8) or (8,9) or (8,7) or (7,8). Two of these are closer to, and two are farther from, his starting point. Does this mean that the calculation for the drunkard’s walk doesn’t work on a rectangular grid? What’s wrong with this argument? Once you’ve found the fallacy, can you derive the analogous distance formula for the drunkard’s walk on a rectangular grid using city block units?
We can answer this question from two points of view. We can treat “distance” as the rectangular city block length, assuming that you can only get from one intersection to another by walking along the streets and avenues, without the possibility of ever traveling “as the crow flies.” In this case, the distance from the starting lamppost at (5,5) to (8,8) is six blocks. The key insight for this situation comes from reader Alex R. Consider a rotated square of any size that has the starting point at its center. The apexes of the square lie along the original street or avenue, and for each of these four points, three of the four available paths take the drunkard farther away from the starting point, and only one takes him closer. For instance, from (5,7), which is two blocks from (5,5), you can go to (5,8), (4,7) or (6,7), which are all three blocks away from (5,5). Only the southward (5,6) path ends up one block away. The example location (8,8) given in the problem does indeed have an equal number of paths leading toward the lamppost and away from it, and this is true of the bulk of the points the drunkard visits. But there always exists the finite possibility that the drunkard is at one of the apexes of the rotated square centered on the starting point, and hence he always has a net movement away from the lamppost, no matter what his distance from the lamppost.
How much is this outward movement on average? Here is a simple calculation that estimates this for a single step taken from a given point, without bothering to relate it to the number of steps required to get there. Consider the diamond-shaped rotated square centered on (5,5) shown highlighted in the figure above. It includes four grid points similar to (5,7) with three outward paths and one inward path as shown, and four other points like (4,6) that have two inward and two outward paths, for a total of 8 points with 32 possible paths. For 20 of these paths, the distance from the lamppost after the next block walk will increase to three blocks, and for 12 paths, the distance will decrease to one block. The average outward distance is therefore 72/32 or 2.25 blocks — an increase of one-fourth of a block. The general formula for the increase in average distance for a square of size n blocks is simply 1/2n blocks. So, for a drunk who is on a point that lies on a 2-by-2 square from the starting point, the average increase in distance is one-fourth of a block, and for one who is on a 4-by-4 square, the average increase falls to one-eighth of a block. As with the more general distance formula of the unrestricted drunkard’s walk, the increase in average distance takes place ever more slowly the farther the drunk moves from the starting point. This is the same process that underlies diffusion: the rate at which the sugar or sweetener spreads into your morning tea or coffee. The funny math book that I referred to in the column summed this up with the quip, “Now you can see the advantage of stirring your drink if you are in any kind of hurry.”
If, instead of considering the rectangular city-block distance, you can consider the actual aerial distance, as Tom Nichols and Michael both did very nicely, there is another reason why there is a net outward movement: Outward steps increase this distance more than inward steps decrease it. Amazingly, in this case, you recover the familiar random-walk formula, which states that the mean square distance from the starting point is proportional to the square root of the number of steps. Or, to put it another way, the squared distance increases by one at each step, just as we saw with the circle example in the puzzle column. As Michael put it, this is a pretty robust formula! He showed that it works for rectangular multidimensional grids as well as for non-rectangular grids.
Our second, very interesting puzzle went as follows.
- Assume that the above city has a 0th Street and 0th Avenue (it was designed by computer scientists!). Two coin-collector friends, Sally and Al, arrive in the city by subway, each carrying a stack of silver dollars. They emerge at the corner of 6th Avenue and 5th Street and play the following game. At each intersection they toss two coins to determine randomly which direction they should walk next, out of the four choices available to them. Sally’s goal is to reach 0th Street or 8th Street. Al’s target is 0th Avenue or 8th Avenue. If the random direction chosen gets either Al or Sally closer to their respective targets, the other person pays him or her a dollar. Conversely, if either person’s distance from his or her target increases, that person has to give the other person a dollar. If the random direction is neutral with respect to the distance from either target, no money is exchanged. The game ends when one of them reaches his or her target. Notice that at the beginning, Al is closer to 8th Avenue than Sally is to 8th Street, but if he reaches it directly with two lucky westward walks, he will win only $2. Sally is farther from her targets but can potentially win more by the end of the game, because she can improve her position more times. Whom does this game favor in the long run?
The simplest method of solving this was perfectly illustrated by Wiley. Here’s how it works.
We use the two provided hints, which simplify the problem considerably. Let’s apply them to find Al’s payoff at each point on the grid.
Hint 1: Use the idea of symmetry and mirror-image intersections. What would the probabilities be when the street and avenue numbers are equal?
Symmetry tells us that when the pair is on the diagonals of the 8-by-8 square (street number = avenue number, or street number + avenue number = 8) Al and Sally are both equally far from their respective targets, so their probability of winning must be equal and their expected payoffs will be zero. Also, the payoffs have mirror-image symmetry across 4th street and 4th Avenue.
The payoff for cells at the border of the grid is zero, as the game ends. The above considerations simplify the number of unknowns for the 81 nodes of the 9-by-9 grid to just six, as shown in Wiley’s diagram.
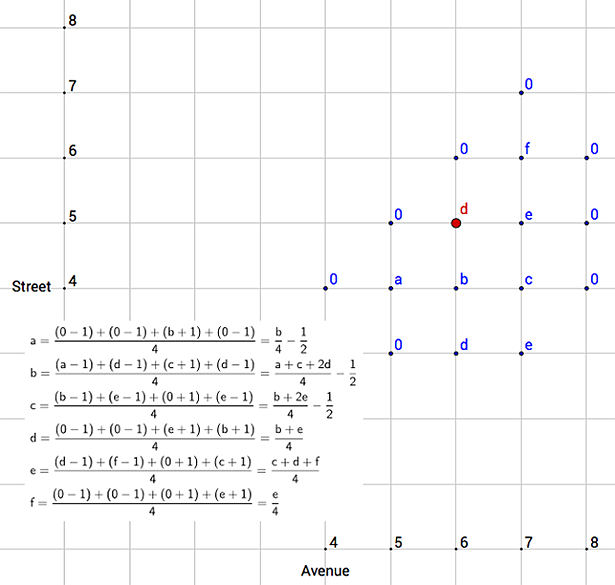
Hint 2: How is the probability at a given intersection related to the probabilities at the four adjacent intersections?
Notice that from any internal point on the grid that Al may be on, the next move takes him to one of its four neighbors with equal probability. Hence the payoff for any given point is equally distributed among its neighbors: It is just the average of the payoffs of the four neighbors to each of which an additional dollar is added or subtracted depending on whether the move to that point was a losing or winning one for Al.
This gives us the six simple equations in six unknowns that are shown. Having worked these out on paper, I guess it’s perfectly fine to use a computer to solve them, though they can be solved manually without too much trouble by substitution. The value of Al’s payoff at d comes out to be –25/68, which comes out to a win for Sally by about 37 cents per game. This is surprising, considering that Al was much closer at the start. In fact, this is true for all possible starting points: The person who is closer to the target loses! Can you figure out the reason for this? Also interesting to consider is the argument made by Marty Green: “At every given coin toss, each player has an equal chance of winning or losing a dollar. It doesn’t matter who reaches their destination first. Throughout the game the odds are equal at every single step, so neither player is favored.” This argument fails. Why?
Later, in a comment, I also added the following variant, in an attempt to even the odds:
What if only the person who reaches his or her target gets the money?
So if their moves were 6,5 → 7,5 → 7,6 → 8,6 reaching 8th Avenue, Al gets $2, Sally gets nothing.
This variant can be solved in the same way as before, as Wiley again demonstrated. It is almost dead even, with Al having the edge by just over one-half a cent per game!
The above method uses simple difference equations to arrive at the answer. As the number of nodes in the grid increases, this method becomes manually intractable. Other methods can be used such as the Markov process used by Tom Nichols. For grids with many millions of nodes, you have to use analytical methods involving the Laplacian or diffusion operator with boundary conditions, or resort to computer simulations.
It is fascinating to exercise the imagination on the relationship of this problem to the processes of thermal or chemical diffusion. Imagine that Al and Sally are nothing but two different temperatures that the opposite walls of a rectangular container are maintained at. Then every point in the container will stabilize at a different temperature between the two. Or, even more fascinating, imagine two different chemicals that are released into a space from vertical and horizontal axes. Every point in the space will have a unique concentration of the two chemicals, like an (x,y) coordinate. In fact, a process similar to this is responsible for the construction of our bodies from the circular ball of cells that we once were. Diffusion processes allow every cell in a particular position to identify where it is and decide whether it needs to become, say, a brain cell or a skin cell in the process of morphogenesis. Furthermore, diffusion and the random walk are responsible for the complex patterning found in the bodies of animals and plants. It’s quite fascinating but not surprising to find that one of the pioneers of this idea as the basis of morphogenesis was the great mathematician Alan Turing.
That’s all for now. The Quanta T-shirt for this puzzle goes to Wiley for his elegant construction of the equations for this solution. Congratulations!
See you soon to explore new insights.



