Researchers Refute a Widespread Belief About Online Algorithms

Nan Cao for Quanta Magazine
Introduction
In life, we sometimes have to make decisions without all the information we want; that’s true in computer science, too. This is the realm of online algorithms — which, despite their name, don’t necessarily involve the internet. Instead, these are problem-solving strategies that respond to data as it arrives, without any knowledge of what might come next. That ability to cope with uncertainty makes these algorithms useful for real-world conundrums, like managing memory on a laptop or choosing which ads to display to people who browse the web.
Researchers study generalized versions of these problems to investigate new methods for tackling them. Among the most famous is the “k-server problem,” which describes the thorny task of dispatching a fleet of agents to fulfill requests coming in one by one. They could be repair technicians or firefighters or even roving ice cream salespeople.
“It’s really simple to define this problem,” said Marcin Bieńkowski, an algorithms researcher at the University of Wrocław in Poland. But it “turns out to be bizarrely difficult.” Since researchers began attacking the k-server problem in the late 1980s, they have wondered exactly how well online algorithms can handle the task.
Over the decades, researchers began to believe there’s a certain level of algorithmic performance you can always achieve for the k-server problem. So no matter what version of the problem you’re dealing with, there’ll be an algorithm that reaches this goal. But in a paper first published online last November, three computer scientists showed that this isn’t always achievable. In some cases, every algorithm falls short.
“I am happy to say that it was a big surprise to me,” said Anupam Gupta, who studies algorithms at Carnegie Mellon University and was not involved in the paper. The work offers “deeper insight into the central problem in this area.”
Computer scientists first outlined this problem in 1988. To get a sense of it, let’s imagine a company that employs plumbers. As calls come in, the company needs to decide which plumber goes to which location. The company’s goal — and the goal of an algorithm for the k-server problem — is to minimize the total distance traveled by all the plumbers.
The tricky part is that the company doesn’t know in advance where the calls will come from. If it did, then it could rely on an “offline algorithm” that knows the future. In particular, it could use an ideal dispatching strategy that finds a solution with the least total travel for any string of calls. No online algorithm can ever beat it, or even reliably match it.
But researchers want to get as close as possible. They measure an online algorithm’s performance by comparing the travel distance in each strategy, calculating what’s known as the competitive ratio. Algorithm designers try to craft online strategies that approach the offline ideal, whittling this ratio down toward 1.
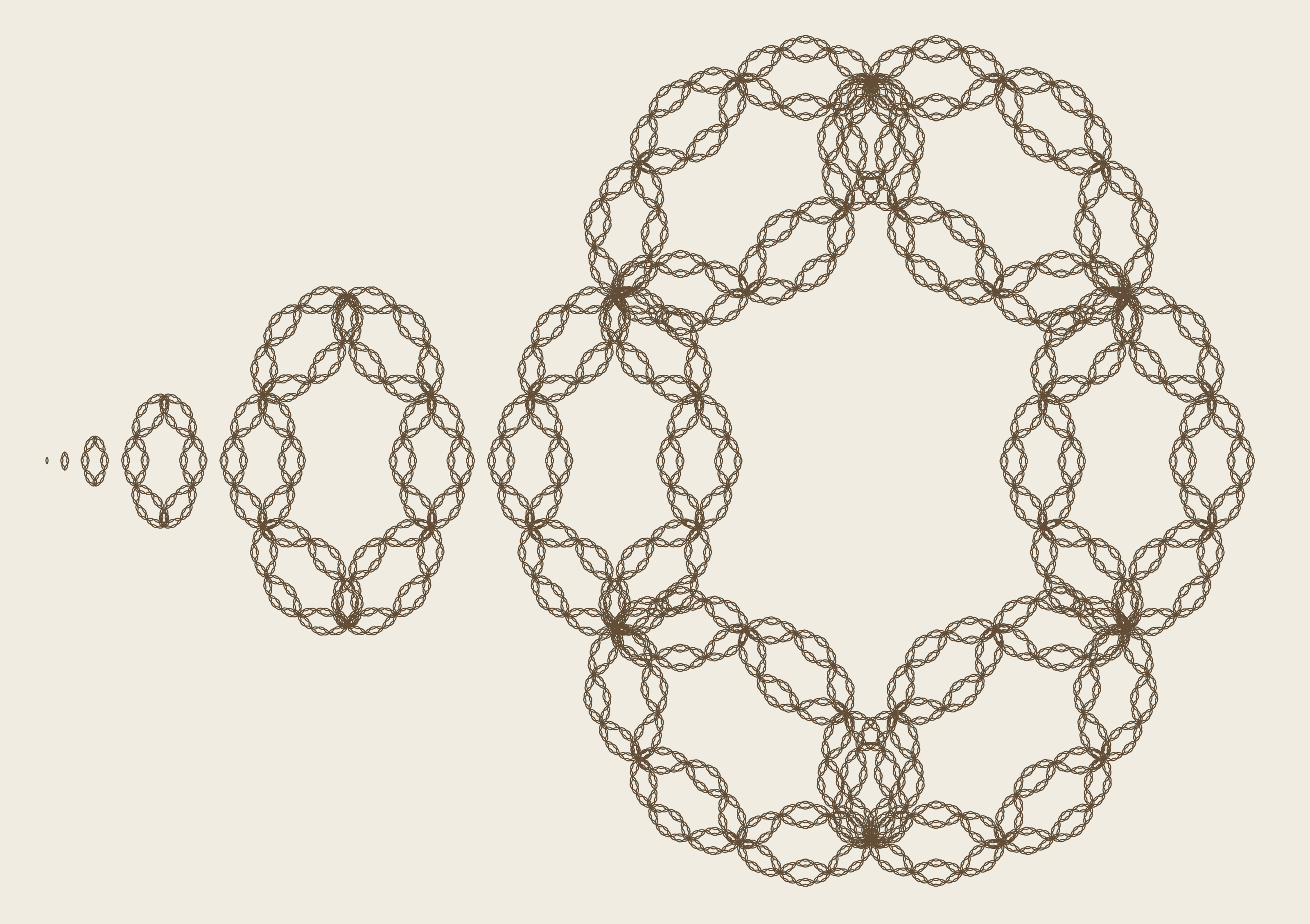
To make sure no algorithm could achieve a competitive ratio of log k, the authors built a family of complex spaces, collections of points that could require an agent to visit; each successive space is made of copies of the last one.
Let’s imagine our plumbing company has just two plumbers, and it only serves a single, long street. The calls come one at a time. A reasonable first approach, known as the greedy algorithm, would be to dispatch whichever plumber is closest to the location of every incoming call. But here’s a scenario where this algorithm struggles: Imagine one plumber starts at the west end of the street and the other at the east end, and all the calls come from two neighboring houses on the west end. In that case, one plumber never moves while the other racks up the miles at those two houses. In retrospect, the best strategy would have been to move both plumbers to the problem-prone area — but, alas, you couldn’t have known where that was going to be.
Even so, Bieńkowski said, it’s possible to do better than the greedy algorithm. The “double coverage” algorithm moves both plumbers at the same rate toward any call that falls between them, until one of them reaches it. This method achieves a lower competitive ratio than the greedy algorithm.
While this abstract problem isn’t relevant for real plumbing companies, “the k-server problem itself is really the defining question” in online computing, said Yuval Rabani, a computer scientist at the Hebrew University of Jerusalem who co-authored the recent paper. In part, that’s because tools and techniques developed during work on the k-server problem often find applications elsewhere in the study of online algorithms, and even outside it.
“This is part of the magic of working on algorithms,” he said.

Yuval Rabani helped disprove a decades-old conjecture about the performance you can expect from certain algorithms.
Aviv Zohar
When they study these problems, scientists like to envision them as games against an adversary. The adversary chooses a devilish sequence of requests to make the online algorithm perform as badly as possible compared to its offline counterpart. To rob the adversary of some of its power, researchers use algorithms that include random decisions.
This strategy is quite effective, and researchers have suspected since the early 1990s that you can always find a randomized algorithm that reaches a specific performance goal: a competitive ratio proportional to log k, where k is the number of agents. This is called the randomized k-server conjecture, and researchers have shown that it’s true for some spaces, or specific collections of points (the equivalent of houses that could call for plumbers). But it hasn’t been proved for all cases.
Like most researchers, Rabani and his co-authors — Sébastien Bubeck of Microsoft Research and Christian Coester of the University of Oxford — figured the conjecture was true. “I had no reason to doubt it,” Coester said.
But that started to change as they worked on another online problem. It had connections to the k-server problem, and the known lower limit on the competitive ratio was unexpectedly high. It made them think perhaps a goal as low as log k for the k-server problem was overly optimistic.
Rabani said it was Coester who first suggested that the randomized k-server conjecture might be false. “As soon as he said it, it all made sense.”
To disprove the conjecture, the authors played the adversary, creating a perfect storm that would prevent any online algorithm from reaching a competitive ratio of log k. Their strategy had two parts: They constructed a family of complex, fractal-like spaces and designed a distribution of request sequences that would be difficult for any possible algorithm. On the algorithm’s very first move, the structure of the space meant it had to choose between two identical paths, one of which would eventually require extra travel based on the requests. Then the authors used a method called recursion to build spaces that multiplied these decision points, forcing the algorithm into a morass of bad options and driving up the cost.
The choices reminded Rabani of the Robert Frost poem “The Road Not Taken,” in which a traveler contemplates two potential paths through a yellow wood. “We just apply the poem recursively,” he joked. “And then things go really bad.”
The authors showed that, in the spaces they had constructed, a randomized algorithm can never achieve a competitive ratio better than (log k)2, pushing a universal goal of log k forever out of reach. They had refuted the conjecture.
This work, which won a Best Paper Award at the 2023 Symposium on Theory of Computing, marks a “solidly theoretical” milestone, Gupta said. This kind of result helps indicate what kind of performance we can hope for from our algorithms. In practice, however, algorithm designers often aren’t planning around worst-case scenarios, with an omnipotent adversary and complete ignorance of the future. When algorithms are unleashed on real-world problems, they often exceed theoretical expectations.
The paper, which also proved cutoffs for randomized algorithms used for other problems, could also have implications for future work in the field. The result clearly “highlights the power” of the technique the authors used, Gupta said.
Perhaps those future findings will defy researchers’ expectations as this one did, Rabani said. “This is one of the cases where it feels really good to be wrong.”



