The theory of eternal inflation casts our universe as one of countless bubbles in an eternally frothing sea.
Olena Shmahalo / Quanta Magazine
Introduction
If modern physics is to be believed, we shouldn’t be here. The meager dose of energy infusing empty space, which at higher levels would rip the cosmos apart, is a trillion trillion trillion trillion trillion trillion trillion trillion trillion trillion times tinier than theory predicts. And the minuscule mass of the Higgs boson, whose relative smallness allows big structures such as galaxies and humans to form, falls roughly 100 quadrillion times short of expectations. Dialing up either of these constants even a little would render the universe unlivable.
To account for our incredible luck, leading cosmologists like Alan Guth and Stephen Hawking envision our universe as one of countless bubbles in an eternally frothing sea. This infinite “multiverse” would contain universes with constants tuned to any and all possible values, including some outliers, like ours, that have just the right properties to support life. In this scenario, our good luck is inevitable: A peculiar, life-friendly bubble is all we could expect to observe.
Many physicists loathe the multiverse hypothesis, deeming it a cop-out of infinite proportions. But as attempts to paint our universe as an inevitable, self-contained structure falter, the multiverse camp is growing.
The problem remains how to test the hypothesis. Proponents of the multiverse idea must show that, among the rare universes that support life, ours is statistically typical. The exact dose of vacuum energy, the precise mass of our underweight Higgs boson, and other anomalies must have high odds within the subset of habitable universes. If the properties of this universe still seem atypical even in the habitable subset, then the multiverse explanation fails.
But infinity sabotages statistical analysis. In an eternally inflating multiverse, where any bubble that can form does so infinitely many times, how do you measure “typical”?
Guth, a professor of physics at the Massachusetts Institute of Technology, resorts to freaks of nature to pose this “measure problem.” “In a single universe, cows born with two heads are rarer than cows born with one head,” he said. But in an infinitely branching multiverse, “there are an infinite number of one-headed cows and an infinite number of two-headed cows. What happens to the ratio?”
For years, the inability to calculate ratios of infinite quantities has prevented the multiverse hypothesis from making testable predictions about the properties of this universe. For the hypothesis to mature into a full-fledged theory of physics, the two-headed-cow question demands an answer.
Eternal Inflation
As a junior researcher trying to explain the smoothness and flatness of the universe, Guth proposed in 1980 that a split second of exponential growth may have occurred at the start of the Big Bang. This would have ironed out any spatial variations as if they were wrinkles on the surface of an inflating balloon. The inflation hypothesis, though it is still being tested, gels with all available astrophysical data and is widely accepted by physicists.
In the years that followed, Andrei Linde, now of Stanford University, Guth and other cosmologists reasoned that inflation would almost inevitably beget an infinite number of universes. “Once inflation starts, it never stops completely,” Guth explained. In a region where it does stop — through a kind of decay that settles it into a stable state — space and time gently swell into a universe like ours. Everywhere else, space-time continues to expand exponentially, bubbling forever.
Each disconnected space-time bubble grows under the influence of different initial conditions tied to decays of varying amounts of energy. Some bubbles expand and then contract, while others spawn endless streams of daughter universes. The scientists presumed that the eternally inflating multiverse would everywhere obey the conservation of energy, the speed of light, thermodynamics, general relativity and quantum mechanics. But the values of the constants coordinated by these laws were likely to vary randomly from bubble to bubble.
Paul Steinhardt, a theoretical physicist at Princeton University and one of the early contributors to the theory of eternal inflation, saw the multiverse as a “fatal flaw” in the reasoning he had helped advance, and he remains stridently anti-multiverse today. “Our universe has a simple, natural structure,” he said in September. “The multiverse idea is baroque, unnatural, untestable and, in the end, dangerous to science and society.”
Steinhardt and other critics believe the multiverse hypothesis leads science away from uniquely explaining the properties of nature. When deep questions about matter, space and time have been elegantly answered over the past century through ever more powerful theories, deeming the universe’s remaining unexplained properties “random” feels, to them, like giving up. On the other hand, randomness has sometimes been the answer to scientific questions, as when early astronomers searched in vain for order in the solar system’s haphazard planetary orbits. As inflationary cosmology gains acceptance, more physicists are conceding that a multiverse of random universes might exist, just as there is a cosmos full of star systems arranged by chance and chaos.
“When I heard about eternal inflation in 1986, it made me sick to my stomach,” said John Donoghue, a physicist at the University of Massachusetts, Amherst. “But when I thought about it more, it made sense.”
One for the Multiverse
The multiverse hypothesis gained considerable traction in 1987, when the Nobel laureate Steven Weinberg used it to predict the infinitesimal amount of energy infusing the vacuum of empty space, a number known as the cosmological constant, denoted by the Greek letter Λ (lambda). Vacuum energy is gravitationally repulsive, meaning it causes space-time to stretch apart. Consequently, a universe with a positive value for Λ expands — faster and faster, in fact, as the amount of empty space grows — toward a future as a matter-free void. Universes with negative Λ eventually contract in a “big crunch.”
Physicists had not yet measured the value of Λ in our universe in 1987, but the relatively sedate rate of cosmic expansion indicated that its value was close to zero. This flew in the face of quantum mechanical calculations suggesting Λ should be enormous, implying a density of vacuum energy so large it would tear atoms apart. Somehow, it seemed our universe was greatly diluted.
Weinberg turned to a concept called anthropic selection in response to “the continued failure to find a microscopic explanation of the smallness of the cosmological constant,” as he wrote in Physical Review Letters (PRL). He posited that life forms, from which observers of universes are drawn, require the existence of galaxies. The only values of Λ that can be observed are therefore those that allow the universe to expand slowly enough for matter to clump together into galaxies. In his PRL paper, Weinberg reported the maximum possible value of Λ in a universe that has galaxies. It was a multiverse-generated prediction of the most likely density of vacuum energy to be observed, given that observers must exist to observe it.
A decade later, astronomers discovered that the expansion of the cosmos was accelerating at a rate that pegged Λ at 10−123 (in units of “Planck energy density”). A value of exactly zero might have implied an unknown symmetry in the laws of quantum mechanics — an explanation without a multiverse. But this absurdly tiny value of the cosmological constant appeared random. And it fell strikingly close to Weinberg’s prediction.
“It was a tremendous success, and very influential,” said Matthew Kleban, a multiverse theorist at New York University. The prediction seemed to show that the multiverse could have explanatory power after all.
Close on the heels of Weinberg’s success, Donoghue and colleagues used the same anthropic approach to calculate the range of possible values for the mass of the Higgs boson. The Higgs doles out mass to other elementary particles, and these interactions dial its mass up or down in a feedback effect. This feedback would be expected to yield a mass for the Higgs that is far larger than its observed value, making its mass appear to have been reduced by accidental cancellations between the effects of all the individual particles. Donoghue’s group argued that this accidentally tiny Higgs was to be expected, given anthropic selection: If the Higgs boson were just five times heavier, then complex, life-engendering elements like carbon could not arise. Thus, a universe with much heavier Higgs particles could never be observed.
Until recently, the leading explanation for the smallness of the Higgs mass was a theory called supersymmetry, but the simplest versions of the theory have failed extensive tests at the Large Hadron Collider near Geneva. Although new alternatives have been proposed, many particle physicists who considered the multiverse unscientific just a few years ago are now grudgingly opening up to the idea. “I wish it would go away,” said Nathan Seiberg, a professor of physics at the Institute for Advanced Study in Princeton, N.J., who contributed to supersymmetry in the 1980s. “But you have to face the facts.”
However, even as the impetus for a predictive multiverse theory has increased, researchers have realized that the predictions by Weinberg and others were too naive. Weinberg estimated the largest Λ compatible with the formation of galaxies, but that was before astronomers discovered mini “dwarf galaxies” that could form in universes in which Λ is 1,000 times larger. These more prevalent universes can also contain observers, making our universe seem atypical among observable universes. On the other hand, dwarf galaxies presumably contain fewer observers than full-size ones, and universes with only dwarf galaxies would therefore have lower odds of being observed.
Researchers realized it wasn’t enough to differentiate between observable and unobservable bubbles. To accurately predict the expected properties of our universe, they needed to weight the likelihood of observing certain bubbles according to the number of observers they contained. Enter the measure problem.
Measuring the Multiverse
Guth and other scientists sought a measure to gauge the odds of observing different kinds of universes. This would allow them to make predictions about the assortment of fundamental constants in this universe, all of which should have reasonably high odds of being observed. The scientists’ early attempts involved constructing mathematical models of eternal inflation and calculating the statistical distribution of observable bubbles based on how many of each type arose in a given time interval. But with time serving as the measure, the final tally of universes at the end depended on how the scientists defined time in the first place.

“People were getting wildly different answers depending on which random cutoff rule they chose,” said Raphael Bousso, a theoretical physicist at the University of California, Berkeley.
Alex Vilenkin, director of the Institute of Cosmology at Tufts University in Medford, Mass., has proposed and discarded several multiverse measures during the last two decades, looking for one that would transcend his arbitrary assumptions. Two years ago, he and Jaume Garriga of the University of Barcelona in Spain proposed a measure in the form of an immortal “watcher” who soars through the multiverse counting events, such as the number of observers. The frequencies of events are then converted to probabilities, thus solving the measure problem. But the proposal assumes the impossible up front: The watcher miraculously survives crunching bubbles, like an avatar in a video game dying and bouncing back to life.
In 2011, Guth and Vitaly Vanchurin, now of the University of Minnesota Duluth, imagined a finite “sample space,” a randomly selected slice of space-time within the infinite multiverse. As the sample space expands, approaching but never reaching infinite size, it cuts through bubble universes encountering events, such as proton formations, star formations or intergalactic wars. The events are logged in a hypothetical databank until the sampling ends. The relative frequency of different events translates into probabilities and thus provides a predictive power. “Anything that can happen will happen, but not with equal probability,” Guth said.
Still, beyond the strangeness of immortal watchers and imaginary databanks, both of these approaches necessitate arbitrary choices about which events should serve as proxies for life, and thus for observations of universes to be counted and converted into probabilities. Protons seem necessary for life; space wars do not — but do observers require stars, or is this too limited a concept of life? With either measure, choices can be made so that the odds stack in favor of our inhabiting a universe like ours. The degree of speculation raises doubts.
The Causal Diamond
Bousso first encountered the measure problem in the 1990s as a graduate student working with Stephen Hawking, the doyen of black hole physics. Black holes prove there is no such thing as an omniscient measurer, because someone inside a black hole’s “event horizon,” beyond which no light can escape, has access to different information and events from someone outside, and vice versa. Bousso and other black hole specialists came to think such a rule “must be more general,” he said, precluding solutions to the measure problem along the lines of the immortal watcher. “Physics is universal, so we’ve got to formulate what an observer can, in principle, measure.”
This insight led Bousso to develop a multiverse measure that removes infinity from the equation altogether. Instead of looking at all of space-time, he homes in on a finite patch of the multiverse called a “causal diamond,” representing the largest swath accessible to a single observer traveling from the beginning of time to the end of time. The finite boundaries of a causal diamond are formed by the intersection of two cones of light, like the dispersing rays from a pair of flashlights pointed toward each other in the dark. One cone points outward from the moment matter was created after a Big Bang — the earliest conceivable birth of an observer — and the other aims backward from the farthest reach of our future horizon, the moment when the causal diamond becomes an empty, timeless void and the observer can no longer access information linking cause to effect.
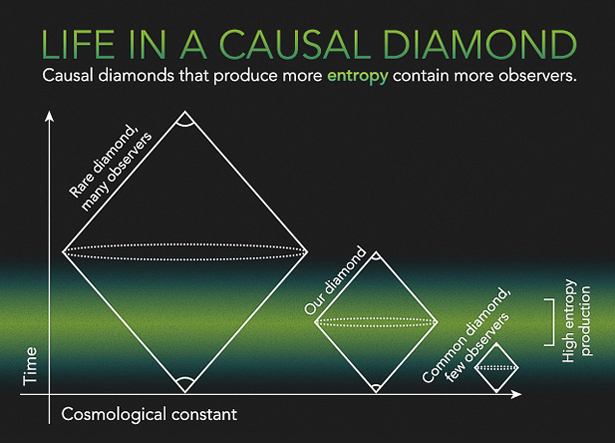
Bousso is not interested in what goes on outside the causal diamond, where infinitely variable, endlessly recursive events are unknowable, in the same way that information about what goes on outside a black hole cannot be accessed by the poor soul trapped inside. If one accepts that the finite diamond, “being all anyone can ever measure, is also all there is,” Bousso said, “then there is indeed no longer a measure problem.”
In 2006, Bousso realized that his causal-diamond measure lent itself to an evenhanded way of predicting the expected value of the cosmological constant. Causal diamonds with smaller values of Λ would produce more entropy — a quantity related to disorder, or degradation of energy — and Bousso postulated that entropy could serve as a proxy for complexity and thus for the presence of observers. Unlike other ways of counting observers, entropy can be calculated using trusted thermodynamic equations. With this approach, Bousso said, “comparing universes is no more exotic than comparing pools of water to roomfuls of air.”
Using astrophysical data, Bousso and his collaborators Roni Harnik, Graham Kribs and Gilad Perez calculated the overall rate of entropy production in our universe, which primarily comes from light scattering off cosmic dust. The calculation predicted a statistical range of expected values of Λ. The known value, 10-123, rests just left of the median. “We honestly didn’t see it coming,” Bousso said. “It’s really nice, because the prediction is very robust.”
Making Predictions
Bousso and his collaborators’ causal-diamond measure has now racked up a number of successes. It offers a solution to a mystery of cosmology called the “why now?” problem, which asks why we happen to live at a time when the effects of matter and vacuum energy are comparable, so that the expansion of the universe recently switched from slowing down (signifying a matter-dominated epoch) to speeding up (a vacuum energy-dominated epoch). Bousso’s theory suggests it is only natural that we find ourselves at this juncture. The most entropy is produced, and therefore the most observers exist, when universes contain equal parts vacuum energy and matter.
In 2010 Harnik and Bousso used their idea to explain the flatness of the universe and the amount of infrared radiation emitted by cosmic dust. Last year, Bousso and his Berkeley colleague Lawrence Hall reported that observers made of protons and neutrons, like us, will live in universes where the amount of ordinary matter and dark matter are comparable, as is the case here.
“Right now the causal patch looks really good,” Bousso said. “A lot of things work out unexpectedly well, and I do not know of other measures that come anywhere close to reproducing these successes or featuring comparable successes.”
The causal-diamond measure falls short in a few ways, however. It does not gauge the probabilities of universes with negative values of the cosmological constant. And its predictions depend sensitively on assumptions about the early universe, at the inception of the future-pointing light cone. But researchers in the field recognize its promise. By sidestepping the infinities underlying the measure problem, the causal diamond “is an oasis of finitude into which we can sink our teeth,” said Andreas Albrecht, a theoretical physicist at the University of California, Davis, and one of the early architects of inflation.
Kleban, who like Bousso began his career as a black hole specialist, said the idea of a causal patch such as an entropy-producing diamond is “bound to be an ingredient of the final solution to the measure problem.” He, Guth, Vilenkin and many other physicists consider it a powerful and compelling approach, but they continue to work on their own measures of the multiverse. Few consider the problem to be solved.
Every measure involves many assumptions, beyond merely that the multiverse exists. For example, predictions of the expected range of constants like Λ and the Higgs mass always speculate that bubbles tend to have larger constants. Clearly, this is a work in progress.
“The multiverse is regarded either as an open question or off the wall,” Guth said. “But ultimately, if the multiverse does become a standard part of science, it will be on the basis that it’s the most plausible explanation of the fine-tunings that we see in nature.”
Perhaps these multiverse theorists have chosen a Sisyphean task. Perhaps they will never settle the two-headed-cow question. Some researchers are taking a different route to testing the multiverse. Rather than rifle through the infinite possibilities of the equations, they are scanning the finite sky for the ultimate Hail Mary pass — the faint tremor from an ancient bubble collision.
Part two of this series, exploring efforts to detect colliding bubble universes, will appear on Monday, Nov. 10.
Correction: This article was revised on November 4, 2014, removing a sentence that did not fully account for recent progress in multiple-parameter calculations of fundamental constants. It was further revised on January 23, 2015, to credit Andrei Linde as the pioneer of the theory of eternal inflation.
This article was reprinted on Wired.com.




