Three Puzzles Inspired by Ramanujan
Srinivasa Ramanujan’s story is part of mathematical folklore, one of the most romantic in the history of mathematics. He started as a poor self-taught clerk in India. Working alone, he discovered highly original and unknown mathematical results that were far ahead of his time. In 1913, he sent a letter filled with strange-looking mathematical theorems to G. H. Hardy, a mathematician at the University of Cambridge. Hardy, one of the world’s leading experts on number theory, later said that “some of [Ramanujan’s theorems] defeated me completely; I had never seen anything in the least like them before.” He was referring to results like the one below.
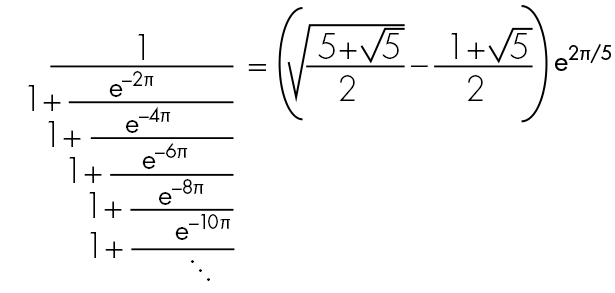
Hardy arranged for Ramanujan to come to England, and the rest is history. The work that Ramanujan did in his brief professional life a century ago has spawned whole new areas of mathematical investigation, kept top mathematicians busy for their whole professional lives, and is finding applications in computer science, string theory, and the mathematical basis of black hole physics.
The mathematician Mark Kac divided all geniuses into two types: “ordinary” geniuses, who make you feel that you could have done what they did if you were say, a hundred times smarter, and “magical geniuses,” the working of whose minds is, for all intents and purposes, incomprehensible. There is no doubt that Srinivas Ramanujan was a magical genius, one of the greatest of all time. Just looking at any of his almost 4,000 original results can inspire a feeling of bewilderment and awe even in professional mathematicians: What kind of mind can dream up exotic gems like these?
Ramanujan indeed had preternatural insights into infinity: he was a consummate bridge builder between the finite and the infinite, finding ways to represent numbers in the form of infinite series, infinite sums and products, infinite integrals, and infinite continued fractions, an area in which, in the words of Hardy, his mastery was “beyond that of any mathematician in the world.” While most of Ramanujan’s results are far beyond the scope of this column, it turns out that we can get a flavor for some simple infinite forms using nothing more than middle-school algebra. Let’s embark on a journey to the infinite.
- Our first question is to prove the following equation involving an infinite nested radical. In 1911, Ramanujan sent the right-hand side of the following equation to a mathematical journal as a puzzle:
If you are intimidated by this at first sight, don’t be! As I mentioned above, you can prove this result with no more than middle-school algebra. All you need is the following elementary result:
(x + 1)2 = x2 + 2x + 1 = x(x + 2) + 1
Rearrange the terms to get: (x + 1)2 = 1 + x(x + 2)
Now if we substitute 2, 3 and 4 for x, we get:
32 = 1 + 2(4), 42 = 1 + 3(5), 52 = 1 + 4(6), …
And believe it or not, that’s all you need to prove the intimidating-looking result above. Can you do it?
- In our second question, we use basic algebra to prove that the famous golden ratio, phi, is equal to the infinite continued fraction shown below.
Again, no need to be intimidated! The neat thing about the continued fraction on the right is that it is self-similar all the way to infinity. That means that you can start anywhere and get exactly the same continued fraction, as shown in the picture below: The continued fraction in the red box is exactly the same as that in the blue box. Yes, as we saw in last month’s column, as far as infinity is concerned, a part can be equal to the whole.
Based on this observed equality, can you set up an equation for the continued fraction and solve it with some elementary algebra to show that it is equal to the golden ratio? Note that this value [(1 + √5)/2] is contained in Ramanujan’s far more elaborate result that Hardy said defeated him completely (top figure).
Our third puzzle was sent to me by the cosmologist Susan Larsen. It was originally published in The Strand Magazine in 1914.
- A certain street has between 50 and 500 houses in a row, numbered 1, 2, 3, 4, … consecutively. There is a certain house on the street such that the sum of all the house numbers to the left side of it is equal to the sum of all the house numbers to its right. Find the number of this house.
The story behind this problem is as follows. A friend of Ramanujan, P. C. Mahalanobis, who was also a student at Cambridge and who later became an eminent statistician, read about this problem while visiting Ramanujan. Ramanujan was in the kitchen, cooking. Mahalanobis solved the problem, and then turned to Ramanujan and said, “Here’s a problem for you.” “What problem? Tell me,” said Ramanujan, still stirring vegetables. Mahalanobis read the problem. Ramanujan immediately said, “Take down the solution.” He then dictated a continuous fraction that expressed all the infinite solutions to the problem if you ignore the constraint of 50 to 500 houses.
So as a bonus problem, can you emulate Ramanujan and find a formula that generates this general solution?
That’s it for the mathematical puzzles. The true puzzles of Ramanujan’s ability are psychological, and I’d love to get the views of Quanta readers on these.
What if Ramanujan had modern calculating tools? Ramanujan, like many other great mathematical geniuses such as Gauss, loved to play with specific cases, which he then built into general results. These geniuses did prodigious calculations by hand — Ramanujan used chalk on slate in his early days, erasing intermediate results with his elbow. Steven Wolfram has conjectured that if Ramanujan had modern calculating tools like Mathematica, “he would have been quite an adventurer — going out into the mathematical universe and finding all sorts of strange and wonderful things, then using his intuition and aesthetic sense to see what fits together and what to study further.” What do you think?
Where do you think Ramanujan’s results came from? When Mahalanobis asked him how he arrived at his solution to problem 3 above, Ramanujan reportedly said, “As soon as I heard the problem, I knew the answer was a continued fraction. I asked myself, ‘Which continued fraction?’ and the answer just came to me.”
How would 21st-century mathematics be different had Ramanujan lived a life of normal length? Tragically, Ramanujan died at age 32, after only about six years as a professional mathematician, during which his output was stupendous. The question has to be asked about all great mathematicians who died young (notably Évariste Galois, inventor of group theory, who died at 20 in a gun duel). How much poorer is the world of mathematics because of Ramanujan’s untimely death?
Happy puzzling! I look forward to your answers.
Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt. And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION” (it will not appear online, so solutions to the puzzle above should be submitted separately).
Note that we may hold comments for the first day or two to allow for independent contributions.
Correction: This post was revised on July 14 to remove an extraneous “1+” in the first line of the continued fraction and an apocryphal reference to a dream of Ramanujan’s.
Correction: This post was revised on July 15 to say that Évariste Galois died in a gun duel at the age of 20, not 21.
Update: The solution has been published here.




