Solution: ‘The Road Less Traveled’

In this month’s Insights puzzle, we discussed a common frustration felt by drivers — of being stuck on the more crowded of two roads while the traffic on the other road whizzes by. We discussed some statistical and psychological reasons for this, and presented two mathematical problems arising out of this situation. As usual, Quanta Magazine readers nailed the problems, and they also suggested some other convincing reasons for this phenomenon.

The first problem went as follows:

If I want to drive from my home in Connecticut to the Quanta Magazine offices in New York, I have two perfectly good roads to follow: the interstate highway I-95, or the picturesque Merritt Parkway. Let us say the drivers of 200 cars independently and randomly make their choice between these two roads with a 50 percent probability of choosing a given road. Assume that there are no other cars on the road. How many more of the 200 cars end up on the more crowded road?

This problem was solved by readers eJ, Tom Nichols and Slipper.Mystery. The answer is that given random driver choice with the same degree of probability, there will be 11.27 more cars on the more crowded road. That is, the more crowded road will have an average of 105.635 cars and the less crowded one will have 94.365 cars. Of course, the average number of cars on each road will be 100, but each road will be slightly more crowded than the other by 11.27 cars on average about half the time.

Here’s a step-by-step explanation:

The first step is to recognize that the probability of a specific number of cars on each road is given by the binomial distribution — the same one that gives you the probability of getting a specified number of heads or tails in a series of coin tosses. Pascal’s triangle gives the binomial coefficients, and we’re going to need an extra-large one with 201 levels. The probability of exactly j cars on a given road is calculated by the formula: the binomial coefficient (n choose j) divided by 2ⁿ, or, in our case, (200 choose j)/2²⁰⁰. As an example, the probability of having exactly 100 cars is 0.056 — this perfectly balanced situation will only happen 1 in 18 times.

The next step is to multiply this probability by the excess of cars on the more crowded road. If the road we’re looking at has j cars, the other has 200 – j. The number of extra cars on the more crowded road is simply the absolute value of the difference between these numbers: |j – (200 – j)|. Multiplying this by the probability of having j cars that we obtained in step 1 gives the expected number of extra cars for each j.

The third step is to add all the expectation numbers for each possible case from 0 to 200, and voila, we will have our answer. In mathematical notation we need to calculate:

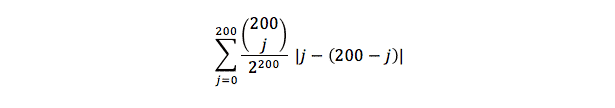
A hundred years ago you would have had to calculate all these numbers by hand and add them manually. No longer! We are amazingly fortunate to live in a world with powerful mathematical tools right at our fingertips. These tools can do all the grunt work. All you have to do is understand the mathematical concepts and master the input syntax of your particular tool of choice. You can do the above calculation using three columns in a spreadsheet like Excel, or in a single loop using a programming language as Slipper.Mystery did. I’d like to urge you to explore the insanely powerful free online tool Wolfram Alpha. Here’s how you’d do it in Wolfram Alpha:

For the first step, you can use Wolfram Alpha’s binomial coefficient function to get the probability, building up your input like this:

First you enter:

binomial(200,j)/2^200

For the second step, multiply the above by the following:

abs(j-(200-j))

For the third step, put everything inside the sum function, and specify j from 0 to 200.

The entire input is this single line:

sum{([binomial(200,j)]/2^200)*abs[j-(200-j)]}, j from 0 to 200

(Note that the braces, brackets and parentheses are interchangeable and I’ve just intermixed the different types for clarity.)

Here’s what the monster spits out:

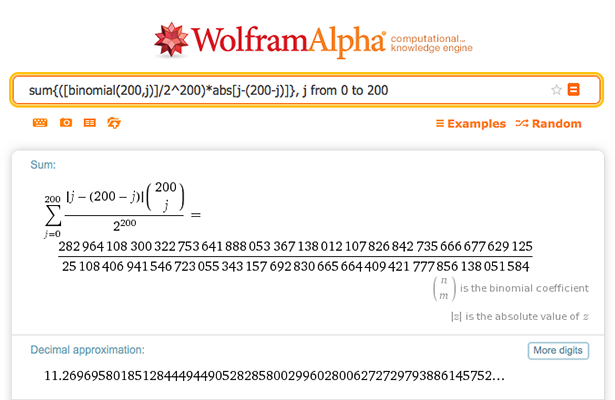
Wolfram Alpha nicely translates the query into mathematical notation, so you can check that that’s what you really wanted. And it is — the summed fraction is algebraically identical to the one we obtained above, with a trivial rearrangement: The absolute value term is incorporated in the numerator and placed before the binomial coefficient. Apart from a slight paucity of digits (!), for which Wolfram Alpha kindly provides a “More digits” button, the output is perfect — something that a mathematician of yore would have given an arm and a leg for. Imagine what Gauss or Ramanujan, both masters at getting general insights by calculating and playing with specific cases, would have achieved with such tools! (Perhaps you would have had to make sure that they were given these tools only after they had already reached the pinnacle of their powers — it may be that those who have never experienced the joy of working with clay and bricks cannot develop the skills to build a house.)

Of course, when you have a calculation in which you have to add 201 terms, mathematicians are always looking for clever and simpler ways to achieve the same result. Sometimes you can achieve the same result using a single, seemingly magical calculation, and when that happens, it points to a deeper insight lurking inside the complexity. A recent example from real science, beautifully described by Natalie Wolchover here in Quanta Magazine, is the amplituhedron, the jewel at the heart of quantum physics.

In our case, the clever trick is to realize that the binomial distribution converges to the Gaussian or normal distribution pretty rapidly as the number of trials gets large. You can then use the properties of normal distributions to get the answer in a single simple calculation. As reader Tom Nichols succinctly explained:

If there are n total cars and the number on road A is k, then the number on road B is n – k and the difference is 2k – n. The difference in cars on the crowded road and the less-traveled road is the absolute value [of] 2k – n or |2k – n|. Given that the distribution of cars on road A (or B) is a binomial distribution with p = 1/2, the mean value of |2k – n| is approximately 2 sqrt(n/2pi). For 200 cars that is about 11.3 more cars on the more crowded road.

Slipper.Mystery elaborated:

For n = 200 and p = 1/2, the binomial distribution becomes close enough to a normal (gaussian) distribution with variance sigma^2 = n * p * (1 – p) = 200 * (1/2) * (1/2) = 50. The expectation value of a half-gaussian with standard deviation sigma is 2 * sigma/sqrt(2 * pi) = 5.64, so the expected difference between the higher and lower roads is twice that, or roughly 11.28.

For the second question we first showed how each driver has a perceived upward bias. When we consider just two cars, each driver sees 1.5 cars instead of one, yielding a perceived bias of 50 percent. The second question asked:

What happens to the driver’s upward bias if there are an average of 100 cars on each road? How many cars do we think he or she sees?

Here again readers quickly figured out that the only reason for the bias is that each driver always counts his or her own car. So the bias does not grow as the number of cars grows, but rather it very quickly decreases to insignificance as a percentage. But is the bias half a car, or is it one car, as some readers thought? The answer is just half a car, as reader Enrique Treviño explained:

If we exclude ourselves, then each road has on average 99.5 cars (because without us, there are 199 cars, so 199/2 cars per road). Therefore, each person sees 100.5 cars on average (the 99.5 plus itself).

Note that these are averages, so it is perfectly justifiable to consider that there are 99.5 other cars on the road, though obviously that can’t really happen. For this problem too, you could calculate 201 different numbers using a formula similar to the one we used for the first problem, and then sum them up. When you do that in Excel, summing a column of 201 unruly-looking numbers with unending decimal places, the sum magically pops out: 100.5 exactly, validating the answer we came up with using simple logic! It never fails to make my spine tingle when complexity melts into simplicity in front of my eyes like this.

Let’s get back to the practical question: What causes the frustrating feeling that we “always” find ourselves on the more crowded road? From the above, it is clear that mathematical explanations cannot account for its intensity and near-universality. Readers came up with some alternative explanations:

1. “Length bias” (Peter Denton): The amount of time that you are on the crowded road is much greater than the amount of time you are on the faster road or lane.
2. “Wrong comparisons” (Colin P): “From one road a driver cannot see the other road, so the comparison he makes is not with the journeys of drivers on the other road at that same time.”
3. “Waves of motion” for multi-lane traffic (Joe): “The ability to move comes in waves that are usually synchronized across lanes. Sometimes, though, particularly when a sudden wave with high amplitude (unusual max speed) comes by, it can hit different lanes at noticeably different times. So, if it hits the lane next to you first, you might change lanes to catch it, only to find yourself stop and watch the lane you were in catch the wave.”

All of these are certainly true in different instances, and no doubt contribute to our negative feelings. But it seems to me that the duration of the delay is not the underlying problem — it’s the psychological effect of really bad experiences that causes the universal feeling of frustration. I remember one time when I was stuck in a traffic jam driving from New York that caused me to miss an important appointment in Stamford, Conn., even though I had allowed three hours for the expected one-hour journey, while a colleague who had used the other road arrived on time. He has probably forgotten the incident, but no doubt he has had upsetting experiences of his own in which he ended up on the wrong road. It is the statistical outliers that shape our feelings of frustration, not the averages.

This puzzle was originally suggested by Amihai Glazer of the University of California, Irvine, and Refael Hassin of Tel Aviv University and published in Barry Nalebuff’s puzzle column in the Journal of Economic Perspectives, volume 4, number 2, pages 177-185. Barry Nalebuff is a professor of economics and management at Yale University and is known in puzzle circles for his contributions to, and comprehensive discussion of, the famous two-envelopes problem. In his discussion of the road problem, Nalebuff noted that the sample bias in our second question becomes larger when the two roads are chosen with unequal probability, and he suggested that this might produce the more crowded feeling. As an extreme example, if all drivers choose the same road, the bias is 100 percent because no one will report the empty road. As Yogi Berra, the baseball player and purveyor of witticisms who died this week, observed, this might happen because of a road’s reputation: “Nobody goes there anymore,” he said once about a restaurant. “It’s too crowded.” Here again, the only way we can get to the truth is to actually sample the road instead of sampling drivers.

The Quanta Magazine T-shirt for this month goes to Tom Nichols, who used the clever and insightful trick detailed above to simplify a lengthy calculation. Thanks to everyone for your high-quality contributions.