Strange Numbers Found in Particle Collisions

Particle collisions are somehow linked to mathematical “motives.”
Xiaolin Zeng for Quanta Magazine
Introduction
At the Large Hadron Collider in Geneva, physicists shoot protons around a 17-mile track and smash them together at nearly the speed of light. It’s one of the most finely tuned scientific experiments in the world, but when trying to make sense of the quantum debris, physicists begin with a strikingly simple tool called a Feynman diagram that’s not that different from how a child would depict the situation.
Feynman diagrams were devised by Richard Feynman in the 1940s. They feature lines representing elementary particles that converge at a vertex (which represents a collision) and then diverge from there to represent the pieces that emerge from the crash. Those lines either shoot off alone or converge again. The chain of collisions can be as long as a physicist dares to consider.
To that schematic physicists then add numbers, for the mass, momentum and direction of the particles involved. Then they begin a laborious accounting procedure — integrate these, add that, square this. The final result is a single number, called a Feynman probability, which quantifies the chance that the particle collision will play out as sketched.
“In some sense Feynman invented this diagram to encode complicated math as a bookkeeping device,” said Sergei Gukov, a theoretical physicist and mathematician at the California Institute of Technology.
Feynman diagrams have served physics well over the years, but they have limitations. One is strictly procedural. Physicists are pursuing increasingly high-energy particle collisions that require greater precision of measurement — and as the precision goes up, so does the intricacy of the Feynman diagrams that need to be calculated to generate a prediction.
The second limitation is of a more fundamental nature. Feynman diagrams are based on the assumption that the more potential collisions and sub-collisions physicists account for, the more accurate their numerical predictions will be. This process of calculation, known as perturbative expansion, works very well for particle collisions of electrons, where the weak and electromagnetic forces dominate. It works less well for high-energy collisions, like collisions between protons, where the strong nuclear force prevails. In these cases, accounting for a wider range of collisions — by drawing ever more elaborate Feynman diagrams — can actually lead physicists astray.
“We know for a fact that at some point it begins to diverge” from real-world physics, said Francis Brown, a mathematician at the University of Oxford. “What’s not known is how to estimate at what point one should stop calculating diagrams.”
Yet there is reason for optimism. Over the last decade physicists and mathematicians have been exploring a surprising correspondence that has the potential to breathe new life into the venerable Feynman diagram and generate far-reaching insights in both fields. It has to do with the strange fact that the values calculated from Feynman diagrams seem to exactly match some of the most important numbers that crop up in a branch of mathematics known as algebraic geometry. These values are called “periods of motives,” and there’s no obvious reason why the same numbers should appear in both settings. Indeed, it’s as strange as it would be if every time you measured a cup of rice, you observed that the number of grains was prime.
“There is a connection from nature to algebraic geometry and periods, and with hindsight, it’s not a coincidence,” said Dirk Kreimer, a physicist at Humboldt University in Berlin.
Now mathematicians and physicists are working together to unravel the coincidence. For mathematicians, physics has called to their attention a special class of numbers that they’d like to understand: Is there a hidden structure to these periods that occur in physics? What special properties might this class of numbers have? For physicists, the reward of that kind of mathematical understanding would be a new degree of foresight when it comes to anticipating how events will play out in the messy quantum world.
Lucy Reading-Ikkanda for Quanta Magazine
A Recurring Theme
Today periods are one of the most abstract subjects of mathematics, but they started out as a more concrete concern. In the early 17th century scientists such as Galileo Galilei were interested in figuring out how to calculate the length of time a pendulum takes to complete a swing. They realized that the calculation boiled down to taking the integral — a kind of infinite sum — of a function that combined information about the pendulum’s length and angle of release. Around the same time, Johannes Kepler used similar calculations to establish the time that a planet takes to travel around the sun. They called these measurements “periods,” and established them as one of the most important measurements that can be made about motion.
Over the course of the 18th and 19th centuries, mathematicians became interested in studying periods generally — not just as they related to pendulums or planets, but as a class of numbers generated by integrating polynomial functions like x2 + 2x – 6 and 3x3 – 4x2 – 2x + 6. For more than a century, luminaries like Carl Friedrich Gauss and Leonhard Euler explored the universe of periods and found that it contained many features that pointed to some underlying order. In a sense, the field of algebraic geometry — which studies the geometric forms of polynomial equations — developed in the 20th century as a means for pursuing that hidden structure.
This effort advanced rapidly in the 1960s. By that time mathematicians had done what they often do: They translated relatively concrete objects like equations into more abstract ones, which they hoped would allow them to identify relationships that were not initially apparent.
This process first involved looking at the geometric objects (known as algebraic varieties) defined by the solutions to classes of polynomial functions, rather than looking at the functions themselves. Next, mathematicians tried to understand the basic properties of those geometric objects. To do that they developed what are known as cohomology theories — ways of identifying structural aspects of the geometric objects that were the same regardless of the particular polynomial equation used to generate the objects.
By the 1960s, cohomology theories had proliferated to the point of distraction — singular cohomology, de Rham cohomology, étale cohomology and so on. Everyone, it seemed, had a different view of the most important features of algebraic varieties.
It was in this cluttered landscape that the pioneering mathematician Alexander Grothendieck, who died in 2014, realized that all cohomology theories were different versions of the same thing.
“What Grothendieck observed is that, in the case of an algebraic variety, no matter how you compute these different cohomology theories, you always somehow find the same answer,” Brown said.
That same answer — the unique thing at the center of all these cohomology theories — was what Grothendieck called a “motive.” “In music it means a recurring theme. For Grothendieck a motive was something which is coming again and again in different forms, but it’s really the same,” said Pierre Cartier, a mathematician at the Institute of Advanced Scientific Studies outside Paris and a former colleague of Grothendieck’s.
Motives are in a sense the fundamental building blocks of polynomial equations, in the same way that prime factors are the elemental pieces of larger numbers. Motives also have their own data associated with them. Just as you can break matter into elements and specify characteristics of each element — its atomic number and atomic weight and so forth — mathematicians ascribe essential measurements to a motive. The most important of these measurements are the motive’s periods. And if the period of a motive arising in one system of polynomial equations is the same as the period of a motive arising in a different system, you know the motives are the same.
“Once you know the periods, which are specific numbers, that’s almost the same as knowing the motive itself,” said Minhyong Kim, a mathematician at Oxford.
One direct way to see how the same period can show up in unexpected contexts is with pi, “the most famous example of getting a period,” Cartier said. Pi shows up in many guises in geometry: in the integral of the function that defines the one-dimensional circle, in the integral of the function that defines the two-dimensional circle, and in the integral of the function that defines the sphere. That this same value would recur in such seemingly different-looking integrals was likely mysterious to ancient thinkers. “The modern explanation is that the sphere and the solid circle have the same motive and therefore have to have essentially the same period,” Brown wrote in an email.
Feynman’s Arduous Path
If curious minds long ago wanted to know why values like pi crop up in calculations on the circle and the sphere, today mathematicians and physicists would like to know why those values arise out of a different kind of geometric object: Feynman diagrams.
Feynman diagrams have a basic geometric aspect to them, formed as they are from line segments, rays and vertices. To see how they’re constructed, and why they’re useful in physics, imagine a simple experimental setup in which an electron and a positron collide to produce a muon and an antimuon. To calculate the probability of that result taking place, a physicist would need to know the mass and momentum of each of the incoming particles and also something about the path the particles followed. In quantum mechanics, the path a particle takes can be thought of as the average of all the possible paths it might take. Computing that path becomes a matter of taking an integral, known as a Feynman path integral, over the set of all paths.
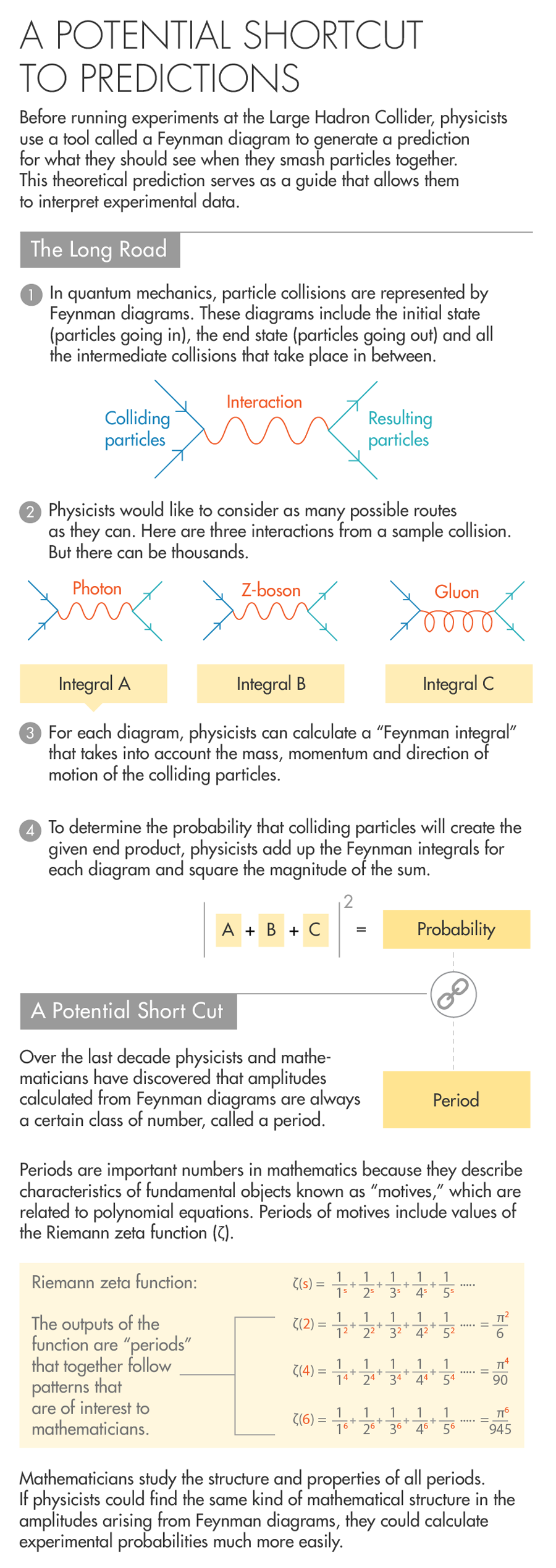
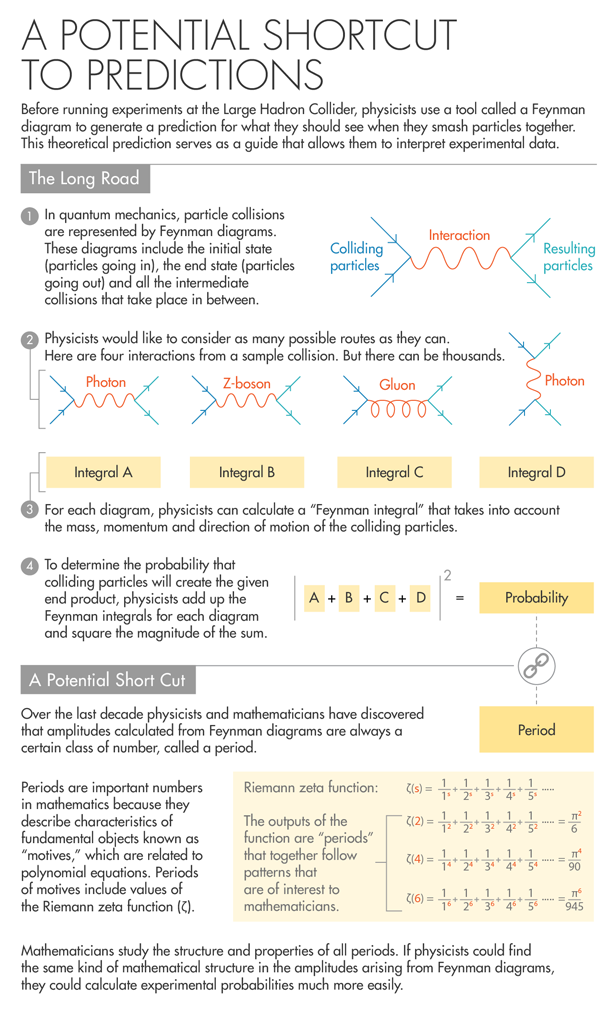
Every route a particle collision could follow from beginning to end can be represented by a Feynman diagram, and each diagram has its own associated integral. (The diagram and its integral are one and the same.) To calculate the probability of a specific outcome from a specific set of starting conditions, you consider all possible diagrams that could describe what happens, take each integral, and add those integrals together. That number is the diagram’s amplitude. Physicists then square the magnitude of this number to get the probability.
This procedure is easy to execute for an electron and a positron going in and a muon and an antimuon coming out. But that’s boring physics. The experiments that physicists really care about involve Feynman diagrams with loops. Loops represent situations in which particles emit and then reabsorb additional particles. When an electron collides with a positron, there’s an infinite number of intermediate collisions that can take place before the final muon and antimuon pair emerges. In these intermediate collisions, new particles like photons are created and annihilated before they can be observed. The entering and exiting particles are the same as previously described, but the fact that those unobservable collisions happen can still have subtle effects on the outcome.
“It’s like Tinkertoys. Once you draw a diagram you can connect more lines according to the rules of the theory,” said Flip Tanedo, a physicist at the University of California, Riverside. “You can connect more sticks, more nodes, to make it more complicated.”
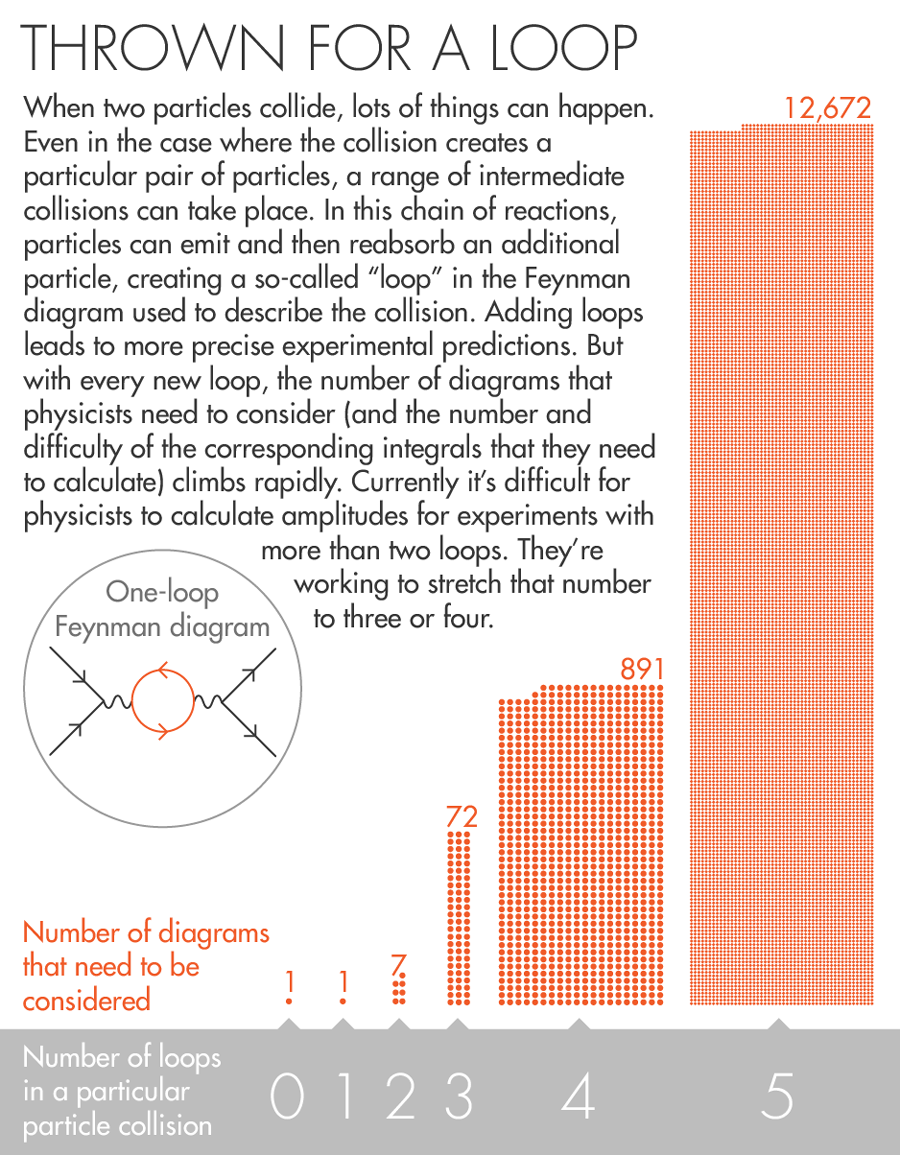
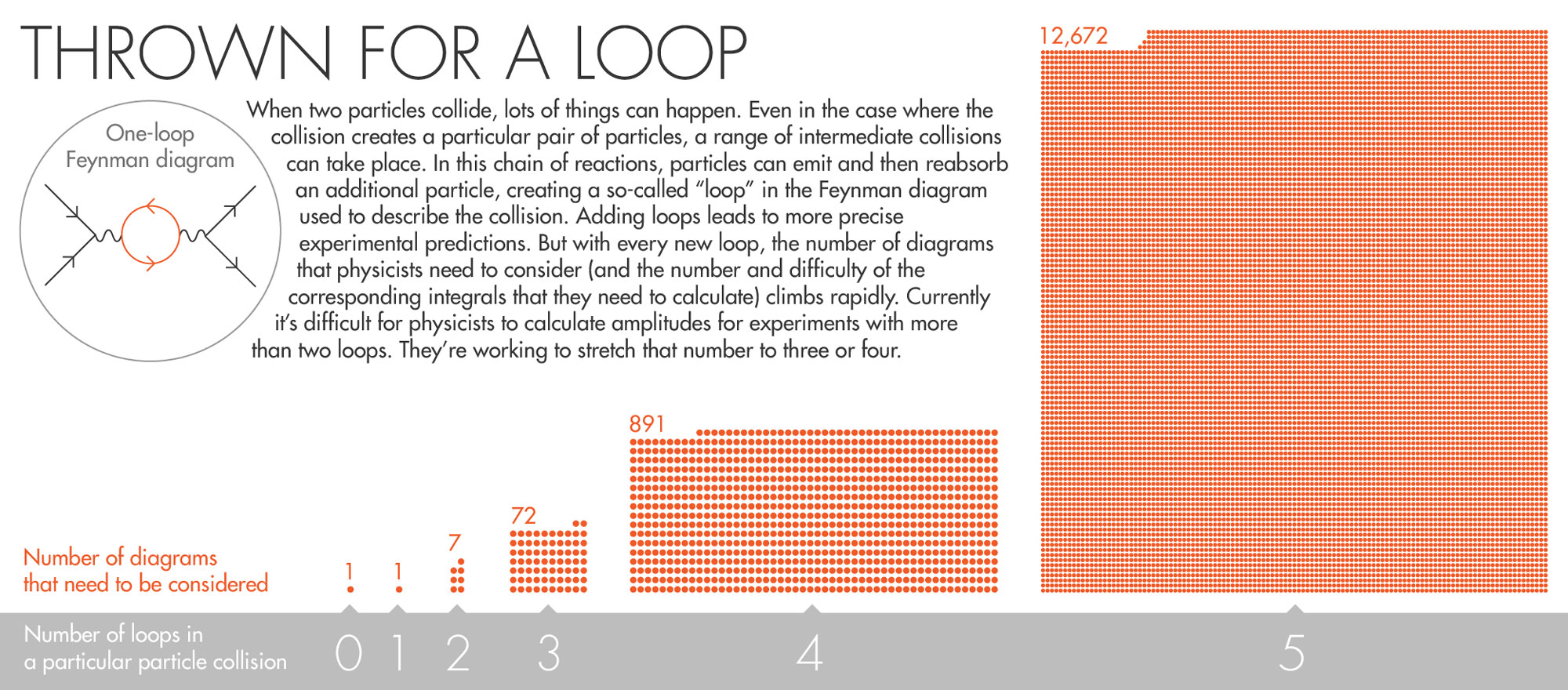
By considering loops, physicists increase the precision of their experiments. (Adding a loop is like calculating a value to a greater number of significant digits). But each time they add a loop, the number of Feynman diagrams that need to be considered — and the difficulty of the corresponding integrals — goes up dramatically. For example, a one-loop version of a simple system might require just one diagram. A two-loop version of the same system needs seven diagrams. Three loops demand 72 diagrams. Increase it to five loops, and the calculation requires around 12,000 integrals — a computational load that can literally take years to resolve.
Rather than chugging through so many tedious integrals, physicists would love to gain a sense of the final amplitude just by looking at the structure of a given Feynman diagram — just as mathematicians can associate periods with motives.
“This procedure is so complex and the integrals are so hard, so what we’d like to do is gain insight about the final answer, the final integral or period, just by staring at the graph,” Brown said.
Lucy Reading-Ikkanda for Quanta Magazine
A Surprising Connection
Periods and amplitudes were presented together for the first time in 1994 by Kreimer and David Broadhurst, a physicist at the Open University in England, with a paper following in 1995. The work led mathematicians to speculate that all amplitudes were periods of mixed Tate motives — a special kind of motive named after John Tate, emeritus professor at Harvard University, in which all the periods are multiple values of one of the most influential constructions in number theory, the Riemann zeta function. In the situation with an electron-positron pair going in and a muon-antimuon pair coming out, the main part of the amplitude comes out as six times the Riemann zeta function evaluated at three.
If all amplitudes were multiple zeta values, it would give physicists a well-defined class of numbers to work with. But in 2012 Brown and his collaborator Oliver Schnetz proved that’s not the case. While all the amplitudes physicists come across today may be periods of mixed Tate motives, “there are monsters lurking out there that throw a spanner into the works,” Brown said. Those monsters are “certainly periods, but they’re not the nice and simple periods people had hoped for.”
What physicists and mathematicians do know is that there seems to be a connection between the number of loops in a Feynman diagram and a notion in mathematics called “weight.” Weight is a number related to the dimension of the space being integrated over: A period integral over a one-dimensional space can have a weight of 0, 1 or 2; a period integral over a two-dimensional space can have weight up to 4, and so on. Weight can also be used to sort periods into different types: All periods of weight 0 are conjectured to be algebraic numbers, which can be the solutions to polynomial equations (this has not been proved); the period of a pendulum always has a weight of 1; pi is a period of weight 2; and the weights of values of the Riemann zeta function are always twice the input (so the zeta function evaluated at 3 has a weight of 6).
This classification of periods by weights carries over to Feynman diagrams, where the number of loops in a diagram is somehow related to the weight of its amplitude. Diagrams with no loops have amplitudes of weight 0; the amplitudes of diagrams with one loop are all periods of mixed Tate motives and have, at most, a weight of 4. For graphs with additional loops, mathematicians suspect the relationship continues, even if they can’t see it yet.
“We go to higher loops and we see periods of a more general type,” Kreimer said. “There mathematicians get really interested because they don’t understand much about motives that are not mixed Tate motives.”
Mathematicians and physicists are currently going back and forth trying to establish the scope of the problem and craft solutions. Mathematicians suggest functions (and their integrals) to physicists that can be used to describe Feynman diagrams. Physicists produce configurations of particle collisions that outstrip the functions mathematicians have to offer. “It’s quite amazing to see how fast they’ve assimilated quite technical mathematical ideas,” Brown said. “We’ve run out of classical numbers and functions to give to physicists.”
Nature’s Groups
Since the development of calculus in the 17th century, numbers arising in the physical world have informed mathematical progress. Such is the case today. The fact that the periods that come from physics are “somehow God-given and come from physical theories means they have a lot of structure and it’s structure a mathematician wouldn’t necessarily think of or try to invent,” said Brown.
Adds Kreimer, “It seems so that the periods which nature wants are a smaller set than the periods mathematics can define, but we cannot define very cleanly what this subset really is.”
Brown is looking to prove that there’s a kind of mathematical group — a Galois group — acting on the set of periods that come from Feynman diagrams. “The answer seems to be yes in every single case that’s ever been computed,” he said, but proof that the relationship holds categorically is still in the distance. “If it were true that there were a group acting on the numbers coming from physics, that means you’re finding a huge class of symmetries,” Brown said. “If that’s true, then the next step is to ask why there’s this big symmetry group and what possible physics meaning could it have.”
Among other things, it would deepen the already provocative relationship between fundamental geometric constructions from two very different contexts: motives, the objects that mathematicians devised 50 years ago to understand the solutions to polynomial equations, and Feynman diagrams, the schematic representation of how particle collisions play out. Every Feynman diagram has a motive attached to it, but what exactly the structure of a motive is saying about the structure of its related diagram remains anyone’s guess.
This article was reprinted on Wired.com.