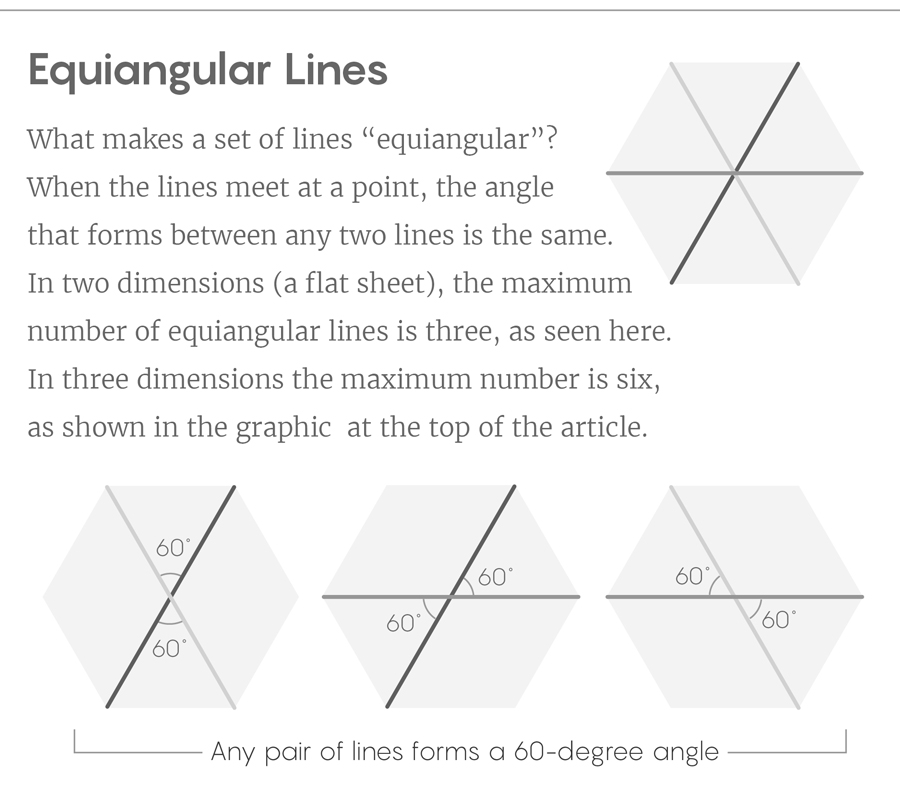
A New Path to Equal-Angle Lines
Introduction
Imagine a set of many lines as in a dream. The lines intersect at a point and radiate outward. There’s something perfect about the way they’re spaced that you can’t quite put your finger on. You start counting them, but before you can finish you wake up with a question hanging on the fringe of your mind: Just how many were there?
For at least 70 years, mathematicians have been trying to answer a question like that one. The sets of lines they’re interested in share a basic feature: Any two lines from the set intersect to form the same angle. Such sets of lines are called “equiangular.” Mathematicians want to know just how big those sets can get as you move past the 3-D space of our everyday experience and into higher dimensions.
Equiangular lines are much more than a curiosity — they’re an almost elemental way to think about geometry. Maximal constructions of equiangular lines often align perfectly with the vertices of highly symmetric shapes, which make them a way to discover the existence of those shapes in the first place. In addition, radiating equiangular lines would pass through the surface of a surrounding sphere at equidistant points. This property makes the lines important for so-called spherical codes, which have important applications in applied mathematics and computer science.
Last spring a team of mathematicians found the maximum number of equiangular lines possible in any dimension, given certain conditions. They proved that that number is much smaller than previous best estimates. Benny Sudakov, a professor of mathematics at the Swiss Federal Institute of Technology Zurich and one of the lead authors, credits the breakthrough to the wide range of mathematical techniques he and his coauthors were able to apply to the problem.
“It’s like when you’re cooking something, we suddenly found we had the right ingredients,” said Sudakov.
Lucy Reading-Ikkanda/Quanta Magazine
To achieve the proof, the mathematicians figured out how to translate the problem into very different mathematical settings. The mathematicians were able to establish properties of equiangular lines in these translated forms that they then carried back into the geometric setting, almost in the way you might retrace your steps to a vision in a dream.
Lines in Many Forms
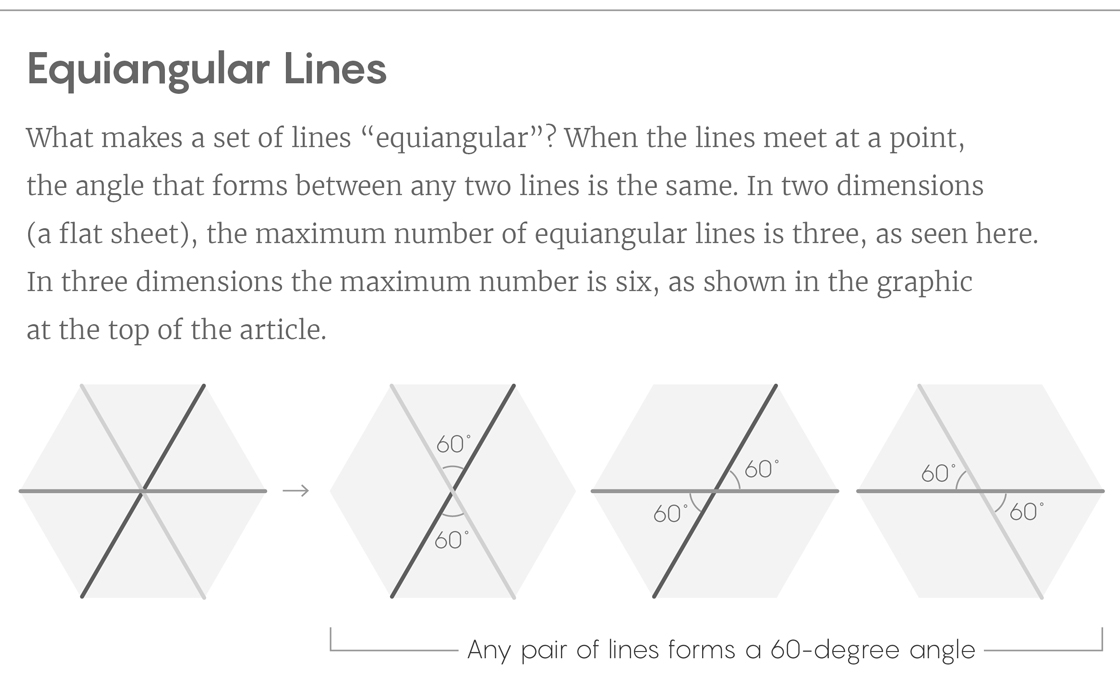
In simple cases, equiangular lines are easy to spot. In two dimensions, take a hexagon and connect opposite vertices. In the resulting construction, any pair of the three lines forms a 60-degree angle. In three dimensions, connecting opposite vertices of an icosahedron (a 3-D shape with 20 faces and 12 vertices) gives you six intersecting lines, any pair of which forms a 63.4-degree angle.
In more than three dimensions, it’s impossible to actually visualize what constructions of equiangular lines would look like, which is one reason it’s been hard to figure out the maximum number of equiangular lines in spaces of any dimension. The best that mathematicians have been able to do is prove that the number of equiangular lines can’t exceed roughly the square of the number of dimensions. (The exact upper bound for dimension d is (d2 + d)/2.) In most dimensions, they know that the number of possible lines is smaller than that.

Benjamin Sudakov
Department of Mathematics, ETH Zurich
Sudakov’s interest in equiangular constructions began in 2015 at a talk given by Boris Bukh, a mathematician at Carnegie Mellon University who’d recently made progress on a refined version of the problem. Bukh had proved that when you specify the size of the angle ahead of time — that is, you ask, what is the maximum number of equiangular lines with, say, a 50-degree angle between any pair of them — the maximum number of equiangular lines is much smaller than the known bound. Instead, it grows in linear fashion, as some constant times the number of dimensions.
Bukh’s result wasn’t elegant — “It wasn’t the best approach in some sense,’’ he said. “I did some ugly things to make my proof work” — but it got Sudakov thinking about the problem. That same year Sudakov spent a semester at the University of Oxford, where he talked through potential lines of attack with Peter Keevash, a mathematician there. Sudakov then returned to Zurich and shared his emerging ideas with his graduate students Igor Balla and Felix Dräxler. They made a suggestion of their own, and suddenly the way to prove a tighter bound on the number of equiangular lines with a specified angle seemed clear. “We all started working on it frantically,” Sudakov said.
Their method was not so different, in spirit, from the way scientists hunt for signatures of an event they can’t observe — they look for traces of the event in other forms. The mathematicians pictured a set of some number of equiangular lines with a specified angle. If the lines were to exist, they could also be represented as other kinds of mathematical objects. The mathematicians proceeded to examine the properties of these analogous objects, knowing that once they understood them, they could work backward from there to the lines themselves.
To see the steps in this approach, it’s helpful to think about how you get from the lines to the analogous objects, even though the actual construction of the lines proceeds in the opposite direction.
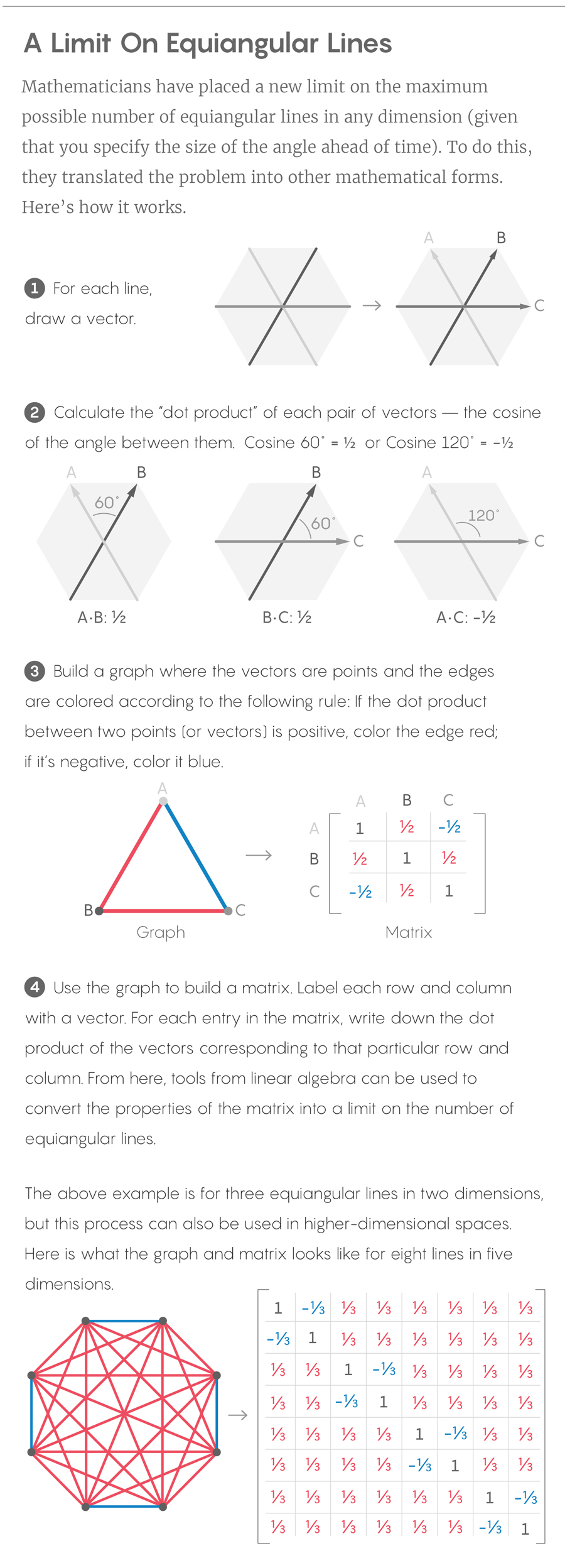

Lucy Reading-Ikkanda/Quanta Magazine
Take a set of equiangular lines. Associate to each line a vector — an object that points in a particular direction. For each line you can imagine two possible vectors, one pointing one way on the line, the other pointing the other way. Choose one, then take the “dot product” of each pair of vectors. If the vectors form an acute angle, the dot product will be positive. If they form an obtuse angle, it will be negative.
The major innovations in the new work appeared after the authors recast the problem in the language of graph theory. Graph theory is the study of how points can be connected to each other by edges. In this scenario, the points of the graph represent the vectors. Points are connected to each other according to this rule: Color the edge between them red if the dot product is positive, blue if the dot product is negative. The result will be a configuration of red and blue lines that provides a different way of looking at the original situation.
“This is another way of encoding the information you’re given, but it’s quite suggestive,” said Keevash. “Once you have a graph, combinatorial ideas come into play.”
In particular, the authors use something called Ramsey’s theorem to bring order to the way all the red and blue edges are joined together. Ramsey’s theorem says that a graph of this sort will always contain large subsets of a certain minimum size that are completely uniform — either all red or all blue. In the case at hand, we know it’s impossible to have many vectors pointing in opposite directions, so the dominant subset of lines will always be red, not blue.
This large subset of red edges forms what Sudakov calls an “anchor” from which he and his collaborators are able to fill out the rest of the graph. By manipulating the remaining vectors, they prove that almost all the vectors not in the subset are joined to the subset via red edges. This, in a sense, casts the blue edges to the outskirts of the graph, and gives the authors a complete, well-ordered picture of what a graphical representation of a set of equiangular lines would look like — if those lines were to exist.
The authors took this arrangement of vectors and further simplified the picture by “projecting” it down into lower dimensions, where additional aspects of their structure came into view.
“It’s a bit like taking a light and shining it on an object and looking at the shadow,” said Jonathan Jedwab, a mathematician at Simon Fraser University in British Columbia who studies equiangular lines. “If you have a three-dimensional object and literally shine a light on it, the shadow it casts on the two-dimensional plane will tell something about what’s going on. If you then moved the 3-D object and shone the light again you could compare the 2-D shadows and learn even more.”
Following the projection, the authors changed settings one final time, reinterpreting their graph as a matrix — a square table of entries. In this table, each entry is a dot product of two vectors. Mathematicians commonly use these kinds of matrices — called Gram matrices — to study configurations of vectors, and in particular those coming from equiangular lines. In this new work, though, the authors had the advantage of first having used Ramsey’s theorem to understand something about the structure of vector relationships.
“After identifying this set, suddenly we cleaned the whole picture and the matrices we got later were much more structured,” said Sudakov.
Through a variety of manipulations, the researchers calculated the “rank” of these structured matrices. Rank is a basic attribute of any matrix. It quantifies, in a sense, how much information the matrix contains, or how many rows you need in order to be able to generate all the rows. (A rough analog of rank would be to count the number of primes needed to express the prime factorization of a number — a number with a longer prime factorization would be considered more complex and have a higher “rank.”)
In this setup, the rank of the matrix is both related to the number of equiangular lines and sets a limit on the number of spatial dimensions in which the lines live. As a result, the authors were able to prove that when you begin by fixing the angle in advance, the maximum number of equiangular lines is 2d – 2 for one particular angle (approximately 70.7 degrees), and no more than 1.93d for any other angle. The authors ended up needing a roundabout process to arrive at such exact numbers, but sometimes it takes a surprising series of recollections to find your way back to last night’s dream.
“My reaction isn’t ‘Why didn’t I think of it?’ It’s ‘My goodness, what an array of tools these people have,’” said Jedwab. “To string these tools together one after another, I think that’s the real ingeniousness of what they’ve done.”




