A New Theory for Systems That Defy Newton’s Third Law

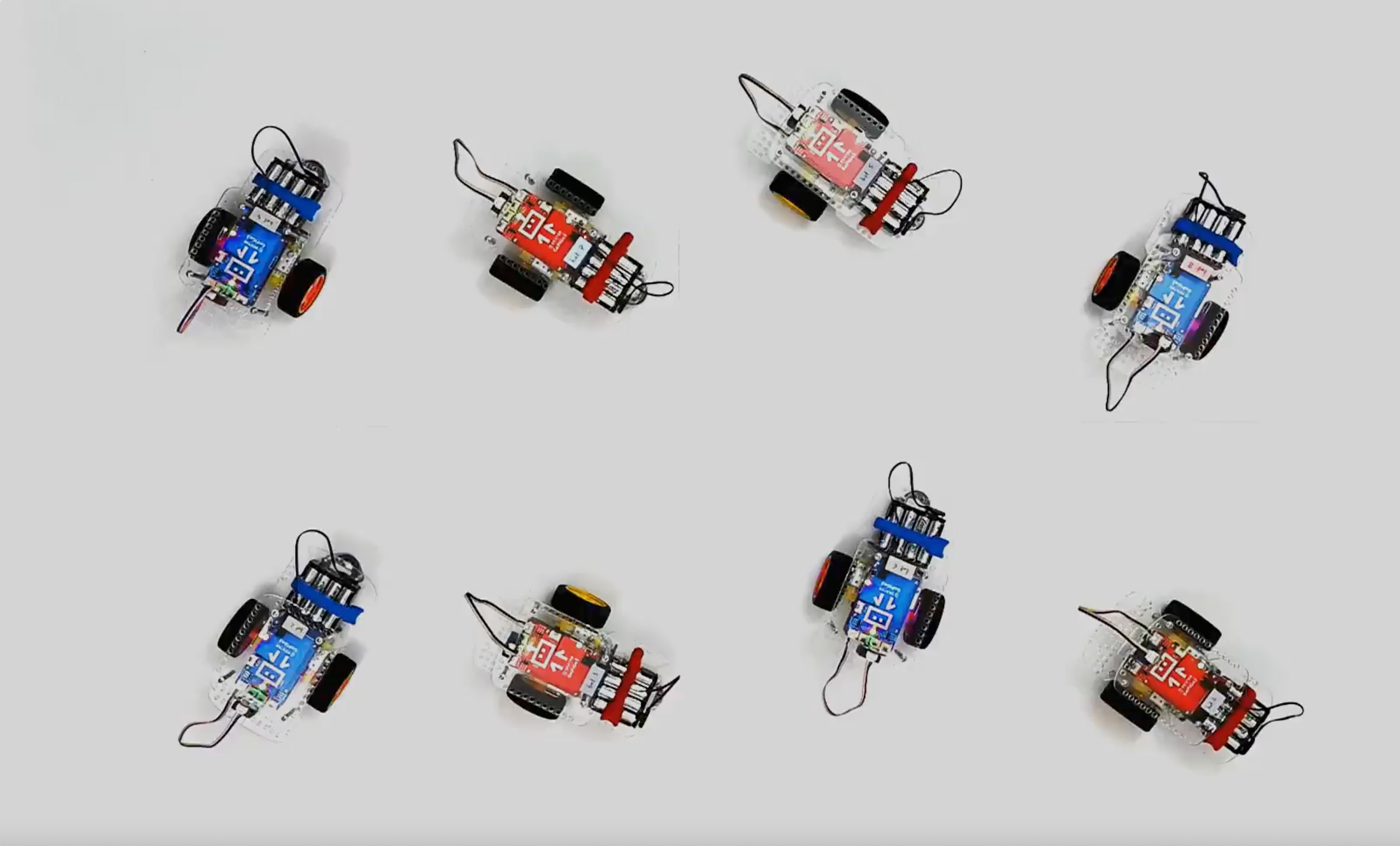
By programming a fleet of robots to behave nonreciprocally — blue cars react to red cars differently than red cars react to blue cars — a team of researchers elicited spontaneous phase transitions.
Kristen Norman for Quanta Magazine
Introduction
Newton’s third law tells us that for every action, there’s an equal reaction going the opposite way. It’s been reassuring us for 400 years, explaining why we don’t fall through the floor (the floor pushes up on us too), and why paddling a boat makes it glide through water. When a system is in equilibrium, no energy goes in or out and such reciprocity is the rule. Mathematically, these systems are elegantly described with statistical mechanics, the branch of physics that explains how collections of objects behave. This allows researchers to fully model the conditions that give rise to phase transitions in matter, when one state of matter transforms into another, such as when water freezes.
But many systems exist and persist far from equilibrium. Perhaps the most glaring example is life itself. We’re kept out of equilibrium by our metabolism, which converts matter into energy. A human body that settles into equilibrium is a dead body.
In such systems, Newton’s third law becomes moot. Equal-and-opposite falls apart. “Imagine two particles,” said Vincenzo Vitelli, a condensed matter theorist at the University of Chicago, “where A interacts with B in a different way than how B interacts with A.” Such nonreciprocal relationships show up in systems like neuron networks and particles in fluids and even, on a larger scale, in social groups. Predators eat prey, for example, but prey doesn’t eat its predators.
For these unruly systems, statistical mechanics falls short in representing phase transitions. Out of equilibrium, nonreciprocity dominates. Flocking birds show how easily the law is broken: Because they can’t see behind them, individuals change their flight patterns in response to the birds ahead of them. So bird A doesn’t interact with bird B in the same way that bird B interacts with bird A; it’s not reciprocal. Cars barreling down a highway or stuck in traffic are similarly nonreciprocal. Engineers and physicists who work with metamaterials — which get their properties from structure, rather than substance — have harnessed nonreciprocal elements to design acoustic, quantum and mechanical devices.
Many of these systems are kept out of equilibrium because individual constituents have their own power source — ATP for cells, gas for cars. But all these extra energy sources and mismatched reactions make for a complex dynamical system beyond the reach of statistical mechanics. How can we analyze phases in such ever-changing systems?
Vitelli and his colleagues see an answer in mathematical objects called exceptional points. Generally, an exceptional point in a system is a singularity, a spot where two or more characteristic properties become indistinguishable and mathematically collapse into one. At an exceptional point, the mathematical behavior of a system differs dramatically from its behavior at nearby points, and exceptional points often describe curious phenomena in systems — like lasers — in which energy is gained and lost continuously.
Now the team has found that these exceptional points also control phase transitions in nonreciprocal systems. Exceptional points aren’t new; physicists and mathematicians have studied them for decades in a variety of settings. But they’ve never been associated so generally with this type of phase transition. “That’s what no one has thought about before, using these in the context of nonequilibrium systems,” said the physicist Cynthia Reichhardt of Los Alamos National Laboratory in New Mexico. “So you can bring all the machinery that we already have about exceptional points to study these systems.”
The new work also draws connections among a range of areas and phenomena that, for years, haven’t seemed to have anything to say to each other. “I believe their work represents rich territory for mathematical development,” said Robert Kohn of the Courant Institute of Mathematical Sciences at New York University.
When Symmetry Breaks
The work began not with birds or neurons, but with quantum weirdness. A few years ago, two of the authors of the new paper — Ryo Hanai, a postdoctoral researcher at the University of Chicago, and Peter Littlewood, Hanai’s adviser — were investigating a kind of quasiparticle called a polariton. (Littlewood is on the scientific advisory board of the Flatiron Institute, a research division of the Simons Foundation, which also funds this editorially independent publication.)
A quasiparticle isn’t a particle per se. It’s a collection of quantum behaviors that, en masse, look as if they should be connected to a particle. A polariton shows up when photons (the particles responsible for light) couple with excitons (which themselves are quasiparticles). Polaritons have exceptionally low mass, which means they can move very fast and can form a state of matter called a Bose-Einstein condensate (BEC) — in which separate atoms all collapse into a single quantum state — at higher temperatures than other particles.
However, using polaritons to create a BEC is complicated. It’s leaky. Some photons continuously escape the system, which means light must be pumped continuously into the system to make up the difference. That means it’s out of equilibrium. “From the theory side, that’s what was interesting to us,” said Hanai.

Phase transitions, such as water freezing, are well understood in systems at equilibrium. But Peter Littlewood (left) and Ryo Hanai, both at the University of Chicago, discovered that in a quantum system with energy continuously pumped in, phase transitions can be understood as singularities known as exceptional points.
Simons Foundation; Courtesy of Ryo Hanai
To Hanai and Littlewood, it was analogous to creating lasers. “Photons are leaking out all the time, but nonetheless you maintain some coherent state,” said Littlewood. This is because of the constant addition of new energy powering the laser. They wanted to know: How does being out of equilibrium affect the transition into BEC or other exotic quantum states of matter? And, in particular, how does that change affect the system’s symmetry?
The concept of symmetry is at the heart of phase transitions. Liquids and gases are considered highly symmetric because if you found yourself hurtling through them in a molecule-size jet, the spray of particles would look the same in every direction. Fly your ship through a crystal or other solid, though, and you’ll see that molecules occupy straight rows, with the patterns you see determined by where you are. When a material changes from a liquid or gas to a solid, researchers say its symmetry “breaks.”
In physics, one of the most well-studied phase transitions shows up in magnetic materials. The atoms in a magnetic material like iron or nickel each have something called a magnetic moment, which is basically a tiny individual magnetic field. In magnets, these magnetic moments all point in the same direction and collectively produce a magnetic field. But if you heat the material enough — even with a candle, in high school science demonstrations — those magnetic moments become jumbled. Some point one way, and others a different way. The overall magnetic field is lost, and symmetry is restored. When it cools, the moments again align, breaking that free-form symmetry, and magnetism is restored.
The flocking of birds can also be viewed as a breaking of symmetry: Instead of flying in random directions, they align like the spins in a magnet. But there is an important difference: A ferromagnetic phase transition is easily explained using statistical mechanics because it’s a system in equilibrium.
But birds — and cells, bacteria and cars in traffic — add new energy to the system. “Because they have a source of internal energy, they behave differently,” said Reichhardt. “And because they don’t conserve energy, it appears out of nowhere, as far as the system is concerned.”
Beyond Quantum
Hanai and Littlewood started their investigation into BEC phase transitions by thinking about ordinary, well-known phase transitions. Consider water: Even though liquid water and steam look different, Littlewood said, there’s basically no symmetry distinction between them. Mathematically, at the point of the transition, the two states are indistinguishable. In a system in equilibrium, that point is called a critical point.
Critical phenomena show up all over the place — in cosmology, high-energy physics, even biological systems. But in all these examples, researchers couldn’t find a good model for the condensates that form when quantum mechanical systems are coupled to the environment, undergoing constant damping and pumping.
Hanai and Littlewood suspected that critical points and exceptional points had to share some important properties, even if they clearly arose from different mechanisms. “Critical points are sort of an interesting mathematical abstraction,” said Littlewood, “where you can’t tell the difference between these two phases. Exactly the same thing happens in these polariton systems.”
They also knew that under the mathematical hood, a laser — technically a state of matter — and a polariton-exciton BEC had the same underlying equations. In a paper published in 2019, the researchers connected the dots, proposing a new and, crucially, universal mechanism by which exceptional points give rise to phase transitions in quantum dynamical systems.
“We believe that was the first explanation for those transitions,” said Hanai.
At about the same time, Hanai said, they realized that even though they were studying a quantum state of matter, their equations weren’t dependent on quantum mechanics. Did the phenomenon they were studying apply to even bigger and more general phenomena? “We started to suspect that this idea [connecting a phase transition to an exceptional point] could be applied to classical systems as well.”
But to chase that idea, they’d need help. They approached Vitelli and Michel Fruchart, a postdoctoral researcher in Vitelli’s lab, who study unusual symmetries in the classical realm. Their work extends to metamaterials, which are rich in nonreciprocal interactions; they may, for example, exhibit different reactions to being pressed on one side or another and can also display exceptional points.
Vitelli and Fruchart were immediately intrigued. Was some universal principle playing out in the polariton condensate, some fundamental law about systems where energy isn’t conserved?
Getting in Sync
Now a quartet, the researchers began looking for general principles underpinning the connection between nonreciprocity and phase transitions. For Vitelli, that meant thinking with his hands. He has a habit of building physical mechanical systems to illustrate difficult, abstract phenomena. In the past, for example, he’s used Legos to build lattices that become topological materials that move differently on the edges than in the interior.
“Even though what we’re talking about is theoretical, you can demonstrate it with toys,” he said.
But for exceptional points, he said, “Legos aren’t enough.” He realized that it would be easier to model nonreciprocal systems using building blocks that could move on their own but were governed by nonreciprocal rules of interaction.
So the team whipped up a fleet of two-wheeled robots programmed to behave nonreciprocally. These robot assistants are small, cute and simple. The team programmed them all with certain color-coded behaviors. Red ones would align with other reds, and the blues with other blues. But here’s the nonreciprocity: The red ones would also orient themselves in the same directions as the blues, while the blues would point in the opposite direction of reds. This arrangement guarantees that no agent will ever get what it wants.
The group scattered the robots across the floor and turned them all on at the same time. Almost immediately, a pattern emerged. The robots began to move, turning slowly but simultaneously, until they were all rotating, basically in place, in the same direction. Rotation wasn’t built into the robots, Vitelli said. “It’s due to all these frustrated interactions. They’re perpetually frustrated in their motions.”
It’s tempting to let the charm of a fleet of spinning, frustrated robots overshadow the underlying theory, but those rotations exactly demonstrated a phase transition for a system out of equilibrium. And the symmetry-breaking that they demonstrated lines up mathematically with the same phenomenon Hanai and Littlewood found when looking at exotic quantum condensates.
To better explore that comparison, the researchers turned to the mathematical field of bifurcation theory. A bifurcation is a qualitative change in the behavior of a dynamical system, often taking the form of one state splitting into two.
Mathematicians draw bifurcation diagrams (the simplest look like pitchforks) to analyze how the states of a system respond to changes in their parameters. Often, a bifurcation divides stability from instability; it may also divide different types of stable states. It’s useful in studying systems associated with mathematical chaos, where small changes in the starting point (one parameter at the outset) can trigger outsize changes in the outcomes. The system shifts from non-chaotic to chaotic behaviors through a cascade of bifurcation points. Bifurcations have a long-standing connection to phase transitions, and the four researchers built on that link to better understand nonreciprocal systems.
That meant they also had to think about the energy landscape. In statistical mechanics, the energy landscape of a system shows how energy changes form (such as from potential to kinetic) in space. At equilibrium, phases of matter correspond to the minima — the valleys — of the energy landscape. But this interpretation of phases of matter requires the system to end up at those minima, says Fruchart.
Vitelli said perhaps the most important aspect of the new work is that it reveals the limitations of the existing language that physicists and mathematicians use to describe systems in flux. When equilibrium is a given, he said, statistical mechanics frames the behavior and phenomena in terms of minimizing the energy — since no energy is added or lost. But when a system is out of equilibrium, “by necessity, you can no longer describe it with our familiar energy language, but you still have a transition between collective states,” he said. The new approach relaxes the fundamental assumption that to describe a phase transition you must minimize energy.
“When we assume there is no reciprocity, we can no longer define our energy,” Vitelli said, “and we have to recast the language of these transitions into the language of dynamics.”
Looking for Exotic Phenomena
The work has wide implications. To demonstrate how their ideas work together, the researchers analyzed a range of nonreciprocal systems. Because the kinds of phase transitions they’ve connected to exceptional points can’t be described by energy considerations, these exceptional-point symmetry shifts can only occur in nonreciprocal systems. That suggests that beyond reciprocity lie a range of phenomena in dynamical systems that could be described with the new framework.
And now that they’ve laid the foundation, Littlewood said, they’ve begun to investigate just how widely it can be applied. “We’re beginning to generalize this to other dynamical systems we didn’t think had the same properties,” he said.
Vitelli said almost any dynamical system with nonreciprocal behaviors would be worth probing with this new approach. “It’s really a step towards a general theory of collective phenomena in systems whose dynamics is not governed by an optimization principle.”
Littlewood said he’s most excited about looking for phase transitions in one of the most complicated dynamical systems of all — the human brain. “Where we’re going next is neuroscience,” he said. He points out that neurons have been shown to come in “many flavors,” sometimes excited, sometimes inhibited. “That is nonreciprocal, pretty clearly.” That means their connections and interactions might be accurately modeled using bifurcations, and by looking for phase transitions in which the neurons synchronize and show cycles. “It’s a really exciting direction we’re exploring,” he said, “and the mathematics works.”
Mathematicians are excited too. Kohn, at the Courant Institute, said the work may have connections to other mathematical topics — like turbulent transport or fluid flow — that researchers haven’t yet recognized. Nonreciprocal systems may turn out to exhibit phase transitions or other spatial patterns for which an appropriate mathematical language is currently lacking.
“This work may be full of new opportunities, and maybe we’ll need new math,” Kohn said. “That’s sort of the heart of how mathematics and physics connect, to the benefit of both. Here’s a sandbox that we haven’t noticed so far, and here’s a list of things we might do.”