Air Traffic Control for Random Surfaces
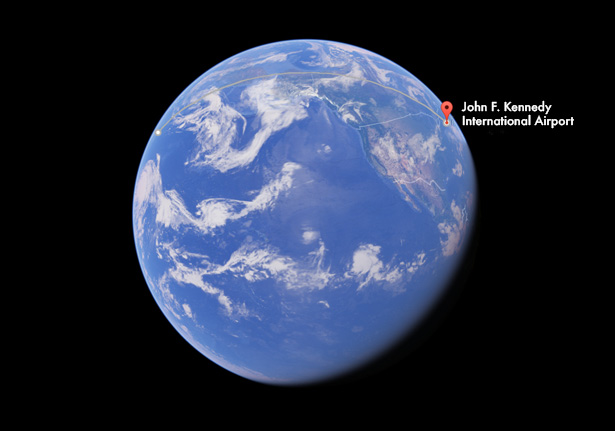
A pilot takes off from New York’s John F. Kennedy airport and flies in a straight line for 14 hours to Tokyo’s Narita airport. Although she flies in a straight line between the two cities, her route would look curved on a flat map. That’s because a straight line on a sphere is not the same shape as a straight line on a piece of graph paper.
And as the randomness of the spiky ball surface increased, the irregularity of the lines would also increase.
As Kevin Hartnett explains in his Quanta Magazine article “A Unified Theory of Randomness,” random shapes occur naturally in the physical world. Random growth models can approximate the way lichen spreads across the surface of a rock, for example. But while finding commonalities among Euclidean geometric objects like lines, squares and cubes is easy, mathematicians have had a harder time describing what different classes of random shapes have in common. In the past few years, though, Scott Sheffield of MIT and Jason Miller of the University of Cambridge have developed a unified theory of randomness. They’ve proven that random shapes can be broken into different classes with distinct properties and that some random objects have clear connections with other kinds of random objects. They’re in the process of publishing a three-paper, comprehensive view of random two-dimensional surfaces.
For more on this story, check out Kevin Hartnett’s article “A Unified Theory of Randomness,” on QuantaMagazine.org.



