At 17, Hannah Cairo Solved a Major Math Mystery

Valerie Plesch for Quanta Magazine
Introduction
It’s not that anyone ever said sophisticated math problems can’t be solved by teenagers who haven’t finished high school. But the odds of such a result would have seemed long.
Yet a paper posted on February 10 left the math world by turns stunned, delighted and ready to welcome a bold new talent into its midst. Its author was Hannah Cairo, just 17 at the time. She had solved a 40-year-old mystery about how functions behave, called the Mizohata-Takeuchi conjecture.
“We were all shocked, absolutely. I don’t remember ever seeing anything like that,” said Itamar Oliveira of the University of Birmingham, who has spent the past two years trying to prove that the conjecture was true. In her paper, Cairo showed that it’s false. The result defies mathematicians’ usual intuitions about what functions can and cannot do.
So does Cairo herself, who found her way to a proof after years of homeschooling in isolation and an unorthodox path through the math world.
A World Without Bounds
Cairo grew up in Nassau, the Bahamas, where her parents had moved so that her dad could take a job as a software developer. She and her two brothers — one three years older, the other eight years younger — were all homeschooled. Cairo started learning math using Khan Academy’s online lessons, and she quickly advanced through its standard curriculum. By the time she was 11 years old, she’d finished calculus.
Soon she had consumed everything that was readily available online. Her parents found a couple of math professors to tutor her remotely — first Martin Magid of Wellesley College, then Amir Aazami from Clark University. But much of her education was self-directed, as she read and absorbed, on her own, the graduate-level math textbooks that her tutors recommended. “Eventually,” Cairo recalled, Aazami “said something like, he feels uncomfortable being paid, because he feels like he’s not really teaching me. Because mostly I would read the book and try to prove the theorems.”

Hannah Cairo taught herself the equivalent of an advanced undergraduate math curriculum by the time she was 14.
Valerie Plesch for Quanta Magazine
But Cairo found homeschooling confining.
“There was this inescapable sameness, in a way. No matter what I did, I was in the same place doing mostly the same things,” she said. “I was very isolated, and nothing I could do could really change that. I’d wake up on certain days and realize, I’m just older.”
Math became a kind of escape, a space that felt expansive when her daily life was not.
“Mathematics was another world I could explore. A world that was not confining, a world I could access at any point just by thinking about it,” she said. “That’s how I grew up, thinking about mathematics as this world of ideas that I can explore on my own. That sort of process helped me see math differently than a lot of people.”
In 2021, amid the Covid pandemic, Cairo’s world began to widen, even as it was narrowing for so many others. Travel restrictions stranded her family at her grandparents’ house in Chicago. While they were there, she joined the Math Circles of Chicago, where teachers and students gather to solve difficult problems together.
The experience led her to apply the following year to a two-week online summer program run by the Berkeley Math Circle, which has nurtured some of the most exceptional math talent in the world. In her application, she listed a set of self-taught subjects that together comprised the equivalent of an advanced undergraduate math degree. She was 14 years old.

As a teenager, Cairo constructed a function that behaved in strange and unexpected ways, disproving a major conjecture in a field called Fourier restriction theory.
Valerie Plesch for Quanta Magazine
“Hannah is above and beyond the ordinary,” said Zvezdelina Stankova, a mathematician at Berkeley and the founder of the Berkeley Math Circle. “Every time she applies for school or a program, she is several levels ahead.”
Yet these scattered experiences never convinced Cairo that she had exceptional mathematical ability. She is soft-spoken, open and humble, and seems genuinely unsure of how her ability stacks up against anyone else’s — in part because for years her only reference point was herself.
“Growing up, I didn’t really know if I was talented,” she said. “I like to play piano, and people around me would tell me that I was really talented at math and at piano. And in retrospect, now that I look at it, I can see, sure, my piano was above average. But it was by no means exceptional. While on the other hand, it looks like mathematically I’m, like, whatever.”
Finding Her Place
In 2023, after a second summer with the Berkeley Math Circle, Cairo wondered what her next step should be. She had already applied to several universities, and while most schools rejected her — she hadn’t finished high school yet — she was accepted by the University of California, Davis. Should she start her undergraduate studies three years early? Or should she pursue educational opportunities elsewhere?
Stankova encouraged her to instead participate in Berkeley’s concurrent enrollment program, where she could take graduate-level math courses from leading researchers in the field.
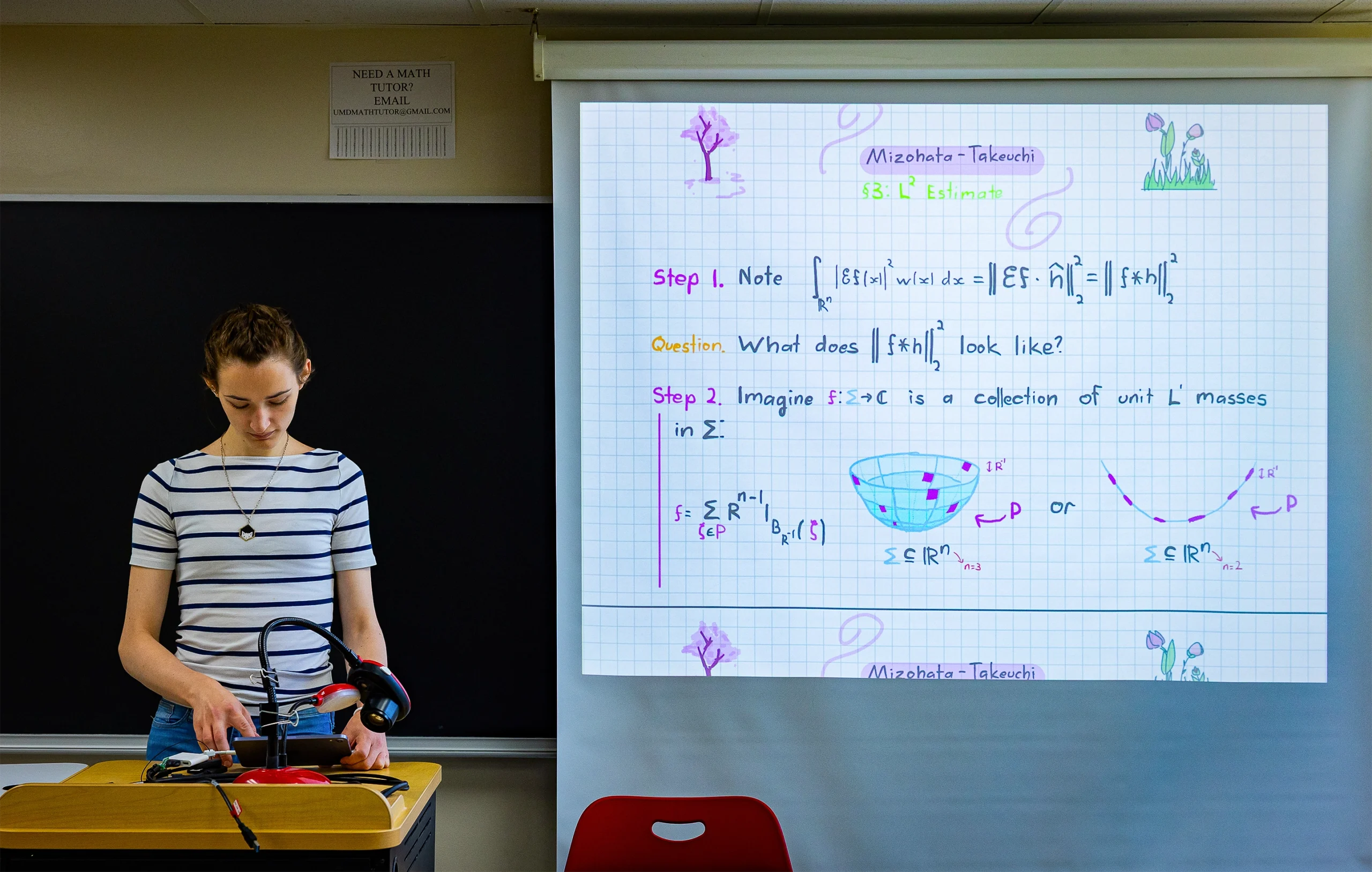
The math world was taken aback when Cairo announced her counterexample to the Mizohata-Takeuchi conjecture — both because it settled a major open problem, and because Cairo was still in high school at the time.
Valerie Plesch for Quanta Magazine
Cairo followed this advice. In the fall of 2023, her family moved to Davis, 60 miles northeast of Berkeley. There, her older brother enrolled as a freshman at UC Davis, and her parents allowed her to commute to Berkeley on Tuesdays and Thursdays. By the spring, she was going five days a week and taking several more classes. She recalls it as a time in her life when she began to feel full of possibility.
“I had started making friends, and I was feeling good,” she said. After the spring semester ended, her family moved from Davis to Berkeley — her brother had decided to transfer there — and Cairo finally felt able to settle in.
Even so, it was an adjustment. “I didn’t have many social experiences, so I still had to learn how to interact with other humans,” she said.
As the 2024–2025 academic year neared, Cairo considered what courses she would take. One class in particular caught her eye — a graduate course in Fourier restriction theory, a branch of harmonic analysis. “It was one of the most advanced analysis classes being offered that semester, so I thought, I’ll just go take it,” she said.

The mathematician Ruixiang Zhang gave Cairo a homework problem that she couldn’t stop thinking about. He later became her adviser.
Lin Lin
The professor for the course was Ruixiang Zhang, an accomplished mathematician whose path into the field had followed a more traditional arc: a gold medal at the 2008 International Mathematical Olympiad, the prestigious high school competition; a doctorate from Princeton University; a postdoc at the Institute for Advanced Study; a tenure-track position at Berkeley, one of the top math departments in the world.
Cairo emailed Zhang, asking to enroll. “Hannah was very focused and seemed to be passionate about the topic,” he said. “This attitude alone is enough for me, so I just gave her permission.”
Within a few weeks, while working on a problem set, she came across a problem that she couldn’t stop thinking about.
Extra Credit
The problem was a simplified version of the Mizohata-Takeuchi conjecture. Zhang had included it in one of his homework assignments as a warm-up, hoping to encourage students to practice advanced techniques in a deep area of math. The assignment also included an optional extension, inviting them to consider whether the proof they’d found for the simplified case could be extended to more complicated formulations of the problem.
Cairo completed the problem set and took Zhang up on the invitation to keep thinking. To her, it seemed natural to follow the thread of an idea as far as it would go. “Why would I stop?” she said.
The Mizohata-Takeuchi conjecture is a problem in harmonic analysis, a field that studies how functions are assembled from wavelike components.
Any given function can be written as the sum of simpler wavelike pieces, called sine waves. Each of those sine waves, in turn, has a frequency. Mathematicians often want to understand the nature of functions that can only be built out of sine waves with certain frequencies. In these cases, the only permitted frequencies are those that satisfy equations that carve out specific surfaces, like a sphere. That’s because the functions that define many physical waves — such as light, sound and quantum particles — are restricted to these kinds of frequencies.

To Cairo, “mathematics was another world I could explore. A world that was not confining, a world I could access at any point just by thinking about it,” she said.
Valerie Plesch for Quanta Magazine
The Mizohata-Takeuchi conjecture considers functions built out of waves whose frequencies lie on such a surface. It states that the energy of the function — a measure of how big the function gets — can only be spread out and concentrated in particular patterns.
It’s as if you’re playing music in a strangely shaped room. Sometimes, the music might echo and amplify, getting very loud. But when that happens, it can only happen in certain spots.
Over the decades, mathematicians made limited progress on a few special cases of the Mizohata-Takeuchi conjecture. But the general problem remained wide open. None of the standard methods seemed able to touch it. That imperviousness made some mathematicians suspect that the conjecture was false; others felt that its elegance made it more likely to be true.
“Some mornings, I’d wake up with the idea that because it’s so simply and elegantly stated, and it’s so broad, in the end it had to be true,” said Tony Carbery, a mathematician at the University of Edinburgh who worked on the problem for decades. “Other mornings, I’d wake up and say … it can’t possibly be true in any simpleminded way.”
Mathematicians found themselves at an impasse.
Exceeding Limits
In the path toward a proof of any hard problem, there’s a lot of doubt. Mathematicians doubt their approaches, doubt their intuitions, doubt that the idea they’re following — so promising in the moment — will actually hold up.
In Cairo’s case, those doubts were amplified. She was new to the field, and her early efforts to prove the full conjecture were tentative and incomplete. She questioned whether she was headed in the right direction. So did Zhang.

Having decided to skip college, Cairo will soon be starting her doctoral studies at the University of Maryland.
Valerie Plesch for Quanta Magazine
“I went to office hours and asked him, ‘Do these ideas work?’ It turned out they didn’t because they were silly,” she said. “There’d be this back-and-forth. I’d come to office hours with new ideas and ask if they work. And he’d say no.”
Cairo kept reading and thinking. Eventually, she found a way to construct a strange, complicated function out of waves whose frequencies all lay on a curved surface — the type of surface the conjecture required. Usually, when you add these kinds of waves together, they interfere, canceling each other out in some places and reinforcing each other elsewhere.
But Cairo showed that in her function, they didn’t cancel out as expected. Instead, their interference created uneven patterns, causing the function’s energy to spread out over some areas and concentrate in others in a fractal-like way that the Mizohata-Takeuchi conjecture prohibited. She found herself staring at a mathematical construction that by many accounts shouldn’t exist.
At first it made her wary. “This is something that happens to me often,” she said. “I come to something that looks like a proof, and I think I have a proof, but [then] I’ve actually been wrong.”
Then two things happened. The first was that she realized she could replace her complicated construction with a much simpler one and achieve the same result.
The other was that she convinced herself, and Zhang, that the result was right.
“Cairo’s paper is a great example of how natural and elegant conjectures can fail in ways we didn’t think of,” Oliveira said. “But to see that, we need to look through the right lenses.”
A New Landscape
The proof, and its unlikely author, have energized the math community since Cairo posted it in February. “I was absolutely, ‘Wow.’ This has been my favorite problem for nigh on 40 years, and I was completely blown away,” Carbery said. “When I found out [Cairo] was much younger than I previously thought, I was much more impressed. The elegance with which the paper is written is quite extraordinary.”
Mathematicians are excited about how Cairo’s work will inspire new research. “I am certain that, from now on, whenever we come upon a problem of similar flavor, we will try to test it against Cairo-like constructions,” Oliveira said.
He and others in the harmonic analysis community will also have to reckon with a changed landscape. In harmonic analysis, there’s a constellation of questions about how the energy of a wave concentrates. If a conjecture known as Stein’s conjecture were true, it would cement connections between some of the most important questions in that broader constellation. But Cairo’s work shows that Stein’s conjecture is false. It eliminates one of the most promising links mathematicians had hoped to establish between different parts of harmonic analysis.
The math world is also adjusting to the fact of Cairo herself. After completing the proof, she decided to apply straight to graduate school, skipping college (and a high school diploma) altogether. As she saw it, she was already living the life of a graduate student. Cairo applied to 10 graduate programs. Six rejected her because she didn’t have a college degree. Two admitted her, but then higher-ups in those universities’ administrations overrode those decisions.
Only the University of Maryland and Johns Hopkins University were willing to welcome her straight into a doctoral program. She’ll start at Maryland in the fall. When she finishes, it will be her first degree.





