Latest Articles
The Mysterious Math of Perfection
Enter the world of perfect numbers and explore the mystery mathematicians have spent thousands of years trying to solve.
The Crooked Geometry of Round Trips
Imagine if we lived on a cube-shaped Earth. How would you find the shortest path around the world?
Some Math Problems Seem Impossible. That Can Be a Good Thing.
Struggling with math problems that can’t be solved helps us better understand the ones we can.
The Simple Math Problem We Still Can’t Solve
Despite recent progress on the notorious Collatz conjecture, we still don’t know whether a number can escape its infinite loop.
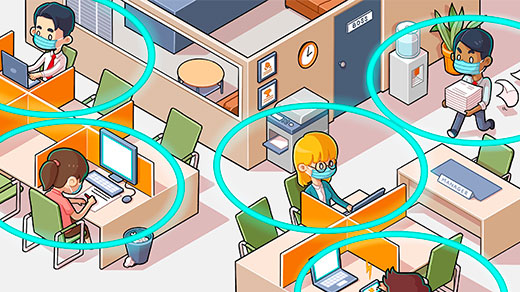
The Math of Social Distancing Is a Lesson in Geometry
How to safely reopen offices, schools and other public spaces while keeping people six feet apart comes down to a question mathematicians have been studying for centuries.
To Win This Numbers Game, Learn to Avoid Math Patterns
Sizing up patternless sets is hard, so mathematicians rely on simple bounds to help answer their questions.
How Rational Math Catches Slippery Irrational Numbers
Finding the best way to approximate the ever-elusive irrational numbers pits the infinitely large against the infinitely small.
How Simple Math Can Cover Even the Most Complex Holes
No one knows how to find the smallest shape that can cover all other shapes of a certain width. But high school geometry is getting us closer to an answer.
Why the Sum of Three Cubes Is a Hard Math Problem
Looking for answers in infinite space is hard. High school math can help narrow your search.