How Rational Math Catches Slippery Irrational Numbers

When my students grow too dependent on their calculators, I ask them to find a number that, when multiplied by itself, gives them 2. Students quickly see that since 1² = 1 and 2² = 4, the answer has to be between 1 and 2. They square 1.1, 1.2, 1.3, and so on and discover that 1.4² = 1.96 and 1.5² = 2.25. “It’s between 1.4 and 1.5,” they say.

“Good to know,” I reply. “But come back when you can tell me exactly what it is.”

It’s fun to eavesdrop as they use their calculators to narrow it down between 1.41 and 1.42, and then again between 1.414 and 1.415. At some point, they start to suspect something’s not right. It’s a trick question: They will never find the exact answer on the calculator, because $latex \sqrt{2}$ is an irrational number.

Rational numbers, which include all integers and all fractions that can be expressed as ratios of integers, are the numbers we usually encounter in everyday life. Our shoe sizes, price tags, ruler markings, basketball stats, recipe amounts — basically all the things we measure or count — are rational numbers. In decimal notation, the representation of a rational number terminates after a certain number of digits (for instance, 3/4 = 0.75) or repeats (for instance, 1/3 is expressed as 0.333…).

Irrational numbers, like $latex \sqrt{2}$ and $latex \pi$, cannot be represented as a ratio of integers. Instead, their decimal representations never terminate and do not repeat. As elusive as they may seem, irrational numbers comprise the vast majority of real numbers, and some of them unlock math’s most important relationships. The area of a circle depends on $latex \pi$, and the irrational number $latex \mathcal{e}$ is central to the study of rates of change.

But in order to make sense of and compute with these numbers, we often have to approximate them. For example, we may not be able to measure $latex \sqrt{2}$ miles exactly, but we can measure 1.4 miles, 1.41 miles and 1.414 miles, which are pretty close.

So the answers students are finding with their calculators are rational approximations of $latex \sqrt{2}$:

1.4 = $latex \frac{14}{10},$ 1.41 = $latex \frac{141}{100},$ 1.414 = $latex \frac{1,414}{1,000},$ 1.4142 = $latex \frac{14,142}{10,000},$ …

Here, each rational approximation of $latex \sqrt{2}$ is closer than the last, but even if we have an infinitely wide calculator and an infinite amount of time, the exact decimal representation of $latex \sqrt{2}$ will always be just out of reach.

To approximate $latex \sqrt{2}$, we can use rational approximations with ever-increasing denominators to get closer and closer to our target. It seems simple enough, but there’s a little magic happening here. Even though we don’t know $latex \sqrt{2}$ exactly, we always seem to know how close our approximations are: 1.4 is off by no more than 0.1; 1.41 is off by no more than 0.01, and so on.

Zooming in on irrational numbers in this way requires using bigger and bigger denominators: $latex \frac{14}{10},$ $latex \frac{141}{100},$ $latex \frac{1,414}{1,000},$ and so on. But a different approach, developed by the German mathematician Gustav Lejeune Dirichlet, generates good rational approximations using relatively small denominators. Dirichlet imagined the rational numbers spread out across the number line, and he figured out how to guarantee that every irrational number would be close to one. Let’s take a look at how he did it.

When students are trying to find $latex \sqrt{2},$ their first rational approximation is 1 = $latex \frac{1}{1}.$ While not very close, it is an easy number to work with, thanks to its simple denominator. What if we allowed ourselves to use the next simple denominator? Rational numbers with denominator 2, like $latex \frac{1}{2},$ $latex \frac{2}{2},$ and $latex \frac{3}{2},$ are evenly spaced along the number line, each $latex \frac{1}{2}$ unit away from the next. This means that every number, rational and irrational, is at most $latex \frac{1}{4}$ away from a rational number of the form $latex \frac{n}{2}$. For example, the interval of numbers between 1 and $latex \frac{3}{2}$ has width $latex \frac{1}{2}$. At its center is the number $latex \frac{5}{4},$ which is $latex \frac{1}{4}$ away from each end, so every number on this interval is at most $latex \frac{1}{4}$ away from either 1 or $latex \frac{3}{2}$. We know $latex \sqrt{2}$ is in this interval, so we know $latex \sqrt{2}$ is at most $latex \frac{1}{4}$ away from a rational number with a denominator of 2.

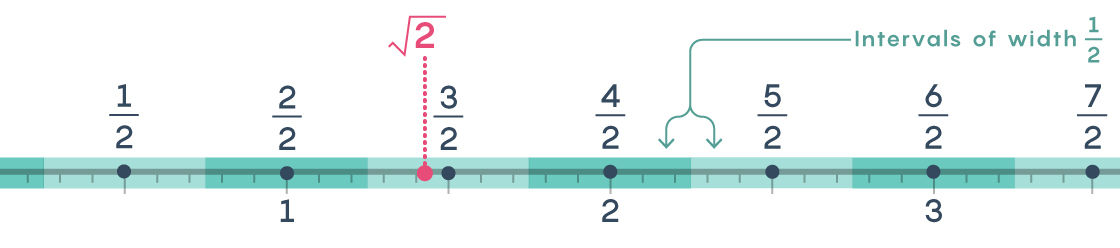
In fact, we can cover the entire number line this way. If we center an interval of width $latex \frac{1}{2}$ at each rational number of the form $latex \frac{n}{2},$ every number, rational and irrational, will lie in one of these intervals.

In red below, we’ve snagged $latex \sqrt{2}$ in one of our intervals, closer to $latex \frac{3}{2}$ than to $latex \frac{2}{2}$ as seen before.

We can also do this using rationals of the form $latex \frac{n}{3}$. The distance between any two such numbers is $latex \frac{1}{3},$ so by centering an interval of width $latex \frac{1}{3}$ on each, we can cover the number line.

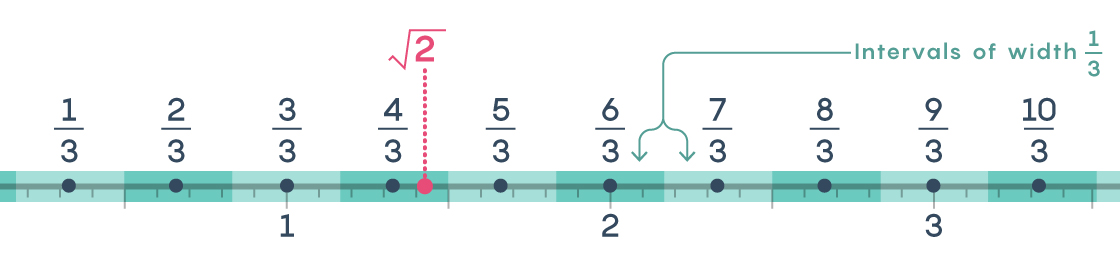
Again, every number, including every irrational number, is in one of these intervals and now is within $latex \frac{1}{6}$ of a rational of the form $latex \frac{n}{3}$. For example, we can see above that $latex \sqrt{2}$ is within $latex \frac{1}{6}$ of $latex \frac{4}{3}$.

But Dirichlet did better. He improved this method by figuring out how to shrink the intervals around their centers while still keeping the entire number line covered. As the intervals shrink, so does the distance to any irrational number we are trying to approximate. This means we’ll get better and better rational approximations, even using relatively small denominators. But we can’t shrink the intervals too quickly: Even though there are infinitely many of them, if the intervals get too small too fast they won’t cover the entire number line. In the battle between the infinitely large and the infinitely small, Dirichlet had to find the right balance to prevent some irrationals from slipping through the cracks.

And he found it. According to Dirichlet’s approximation theorem, when we use rational numbers with denominators no bigger than 3 we know that every irrational number is:

• within $latex \frac{1}{1×3}$ = $latex \frac{1}{3}$ of a rational with denominator 1 (i.e., an integer), or
• within $latex \frac{1}{2×3}$ = $latex \frac{1}{6}$ of a rational with denominator 2, or
• within $latex \frac{1}{3×3}$ = $latex \frac{1}{9}$ of a rational with denominator 3.

Below we see a portion of the number line with intervals of length 2 × $latex \frac{1}{3}$ centered at integers, intervals of width 2 × $latex \frac{1}{6}$ centered at rationals with denominator 2, and intervals of width 2 × $latex \frac{1}{9}$ centered at rationals with denominator 3.

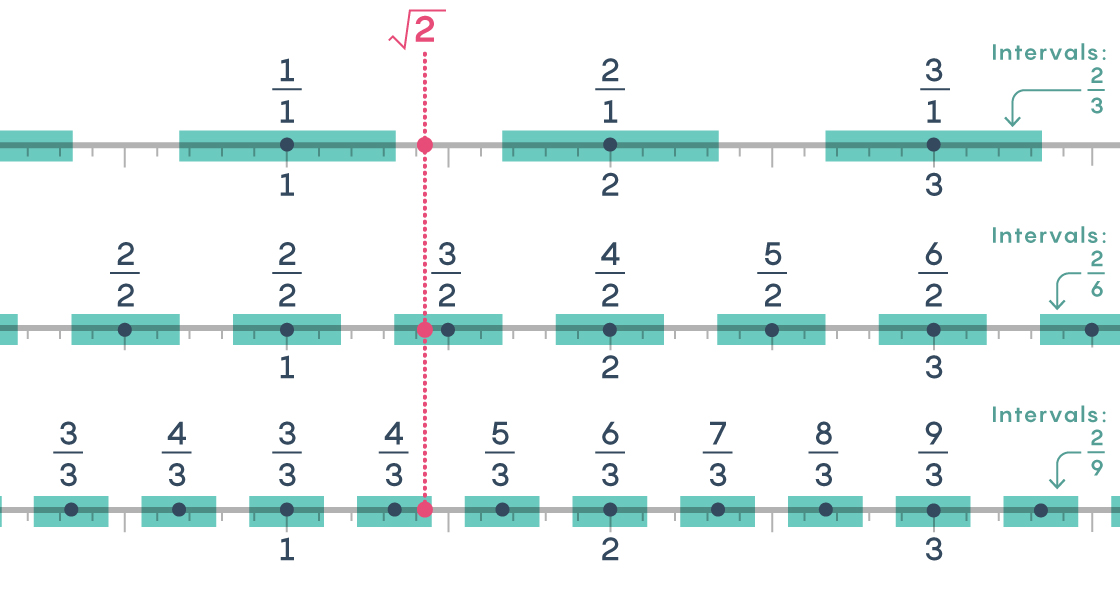
Notice that every part of the number line appears to be covered by some interval. In some cases, by more than one: For example, $latex \sqrt{2}$ is covered by two intervals, which gives rise to two rational approximations that satisfy Dirichlet’s criteria: $latex \frac{3}{2}$ is within $latex \frac{1}{2×3}$=$latex \frac{1}{6}$ of $latex \sqrt{2}$ and $latex \frac{4}{3}$ is within $latex \frac{1}{3×3}$=$latex \frac{1}{9}$ of $latex \sqrt{2}$.

How did Dirichlet know he could shrink the intervals? Well, suppose we wanted to approximate $latex \sqrt{2}$ using rationals with denominators no bigger than 5. Consider the following five irrational numbers

$latex \sqrt{2},$ $latex 2\sqrt{2},$ $latex 3\sqrt{2},$ $latex 4\sqrt{2},$ $latex 5\sqrt{2},$

and look at the beginnings of their decimal representations

1.4142…, 2.8284…, 4.2426…, 5.6568…, 7.0710…

Of the five numbers, the last one is closest to an integer. It isn’t far from 7, a fact we can use to get a rational approximation within Dirichlet’s parameters.

Since $latex 5\sqrt{2}$ – 7 $latex \approx$ 0.0710 and $latex \frac{1}{5}$ = 0.2, we know that $latex 5\sqrt{2}$ is within $latex \frac{1}{5}$ of 7. In other words,

$latex 5\sqrt{2}$ – 7 < $latex \frac{1}{5}$

Now we divide both sides of the inequality by 5:

$latex \frac{5\sqrt{2} – 7}{5}$ < $latex \frac{1}{5×5}$

$latex \sqrt{2}$ – $latex \frac{7}{5}$ < $latex \frac{1}{25}$

This tells us the distance from $latex \sqrt{2}$ to $latex \frac{7}{5}$ is less than $latex \frac{1}{25},$ which satisfies Dirichlet’s criteria. A quick check verifies this, since $latex \sqrt{2}$ – $latex \frac{7}{5}$ $latex \approx$ 0.0142, which is less than $latex \frac{1}{25}$ = 0.04.

Dirichlet proved that, given any irrational number, some multiple of it will be close enough to an integer to yield a rational approximation that satisfies his criteria. That doesn’t mean we can get as close as we want using any denominator of our choosing: After all, if we’re only allowed to use thirds, we can never get closer to $latex \sqrt{2}$ than $latex \frac{4}{3}$. But whatever size we choose for our denominator, our irrational number will always be in one of the small intervals guaranteed by Dirichlet.

For denominators up to 5, Dirichlet’s method guarantees that every irrational number is:

• within $latex \frac{1}{1×5}$ = $latex \frac{1}{5}$ of a rational with denominator 1 (i.e., an integer), or
• within $latex \frac{1}{2×5}$ = $latex \frac{1}{10}$ of a rational with denominator 2, or
• within $latex \frac{1}{3×5}$ = $latex \frac{1}{15}$ of a rational with denominator 3, or
• within $latex \frac{1}{4×5}$ = $latex \frac{1}{20}$ of a rational with denominator 4, or
• within $latex \frac{1}{5×5}$ = $latex \frac{1}{25}$ of a rational with denominator 5.

Here we see how, using denominators up to 5, we get two approximations of $latex \sqrt{2}$ that satisfy Dirichlet’s criteria: $latex \frac{3}{2}$ is within $latex \frac{1}{2×5}$ = $latex \frac{1}{10}$ of $latex \sqrt{2}$ and $latex \frac{7}{5}$ is within $latex \frac{1}{5×5}$ = $latex \frac{1}{25}$ of $latex \sqrt{2}$.

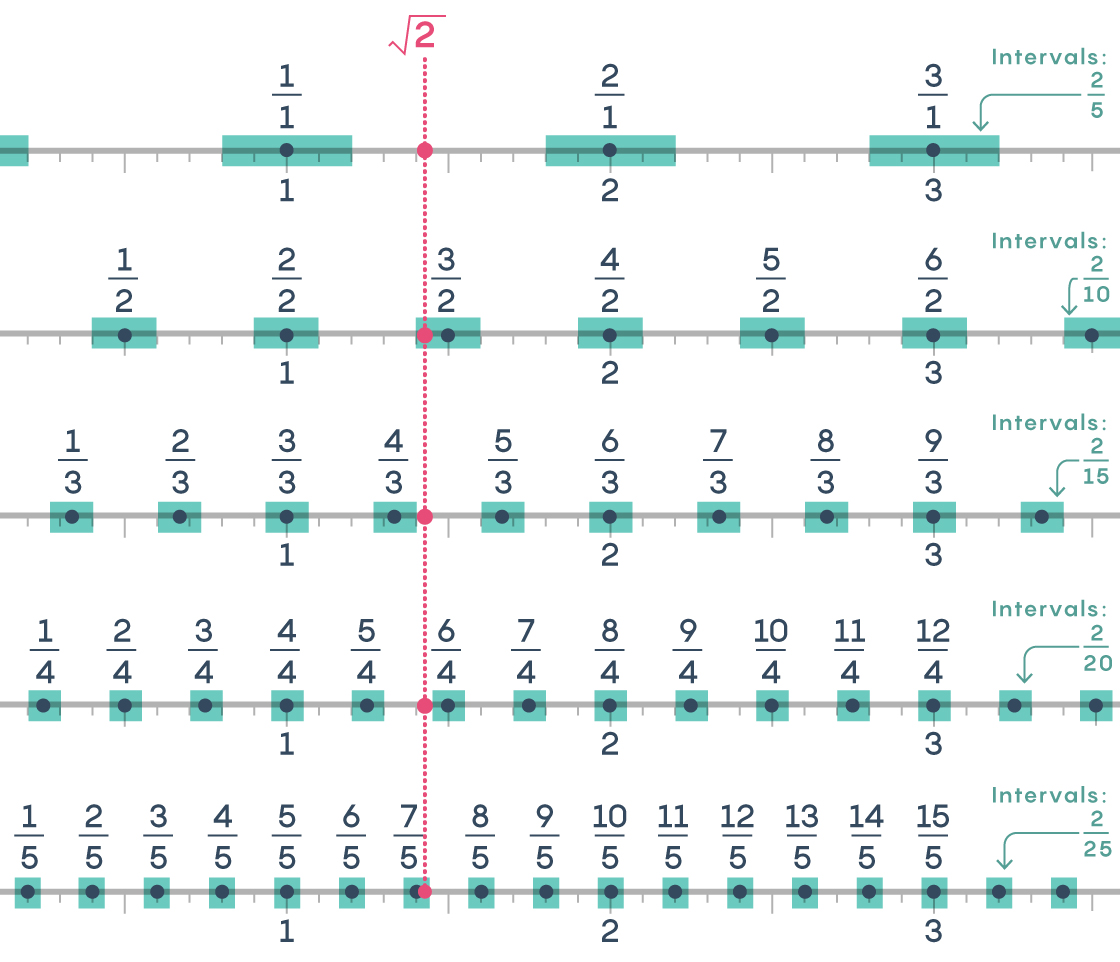
Remember when we found $latex \frac{4}{3}$ to be a good approximation of $latex \sqrt{2}$ ? For denominators up to 3, it satisfied Dirichlet’s criteria: It was within $latex \frac{1}{3×3}$ = $latex \frac{1}{9}$ of $latex \sqrt{2}$. But now when we use denominators up to 5, it doesn’t satisfy the criteria, because it’s not within $latex \frac{1}{3×5}$ = $latex \frac{1}{15}$ of $latex \sqrt{2}$. As we increase the size of allowable denominators, the intervals around each rational number shrink. This inevitably leads us to discard some approximations, but it also guarantees that better approximations (like $latex \frac{7}{5}$) will appear.

This is where the power of covering the entire number line comes in. Even though the infinitely many intervals continuously shrink in size, Dirichlet’s theorem guarantees that each irrational number will be in at least one of them. In our original example, we zoomed in infinitely close on the unknown using rationals with denominators that grew large quickly, like $latex \frac{141}{100},$ $latex \frac{1,414}{1,000},$ and $latex \frac{14,142}{10,000}$. But Dirichlet gets us close with denominators that grow slowly, allowing us to catch good approximations as they pop up along the way.

Dirichlet’s method guarantees that there will always be decent rational approximations to irrational numbers like $latex \sqrt{2}$ and $latex \pi$: For example, $latex \pi$ $latex \approx$ 3.14159265… is famously close to $latex \frac{22}{7}$ = 3.14285714…, and even closer to $latex \frac{355}{113}$ = 3.14159292…. And this isn’t just a matter of approximating specific irrationals like $latex \sqrt{2}$ and $latex \pi$. Since the entire line is covered, every irrational number is guaranteed to be within some controllable distance of a rational. Dirichlet’s net catches them all.

But mathematicians are never satisfied with a technique that just works. They want to know how far they can push it. How small can we make the intervals while still guaranteeing that the entire number line is covered? What happens if we use only certain kinds of rationals and not others? Generalizing Dirichlet’s technique ultimately led researchers to the Duffin-Schaeffer conjecture. First proposed in 1941, the Duffin-Schaeffer conjecture hypothesized that any question of this type can be settled by a single calculation: If the answer turns out to be infinity, the entire number line is essentially covered. If the answer is anything less, the number line is essentially naked.

These questions were settled last year, when Dimitris Koukoulopoulos and James Maynard announced a proof of the Duffin-Schaeffer conjecture. The pair had 80 years of attempts to build on, but as is so often the case in mathematics, it took a new approach to close the gap. Koukoulopoulos and Maynard used techniques from graph theory to hammer out the final details of this number theory result.

While it may not have immediate practical consequences, proving the Duffin-Schaeffer conjecture has settled this latest mathematical battle between the infinitely large and the infinitely small. And it’s always nice to know when close is close enough.