Conducting the Mathematical Orchestra From the Middle

Emily Riehl sees similarities between the roles of the viola in an orchestra and category theory in math.
Schaun Champion for Quanta Magazine
Introduction
Emily Riehl sees similarities between the viola, which she grew up playing, and the mathematical field of higher category theory, in which she is currently a leading participant. She thinks of the two as the “glue” of their respective domains; just as the viola creates a richer orchestral sound, “there’s a sense in which category theory makes mathematics deeper,” she said.
The categorical perspective emerged in mathematics in 1945 when Samuel Eilenberg and Saunders Mac Lane published their radical paper, “General Theory of Natural Equivalences.” It proposed a deeply unconventional idea, arguing that mathematics needed to do away with the equal sign, and the whole simplistic notion of equality, and replace it with the deeper, more sophisticated idea of “equivalence.”
Instead of calling two things exactly equal, Eilenberg and Mac Lane urged mathematicians to embrace sophisticated new mathematical structures that captured the many ways in which two things might be the same, or equivalent.
The proposal was received with skepticism. Riehl, an associate professor of mathematics at Johns Hopkins University, says that many early readers of Eilenberg and Mac Lane’s work wondered, “Is this even mathematics?”
But the doubts didn’t persist for long. Today, category theory and its next-generation version, higher category theory, are central to many fields of math, from algebraic geometry to mathematical physics. In those areas, Riehl said, “I think it would be impossible to describe the kind of basic objects of study without categorical language.”
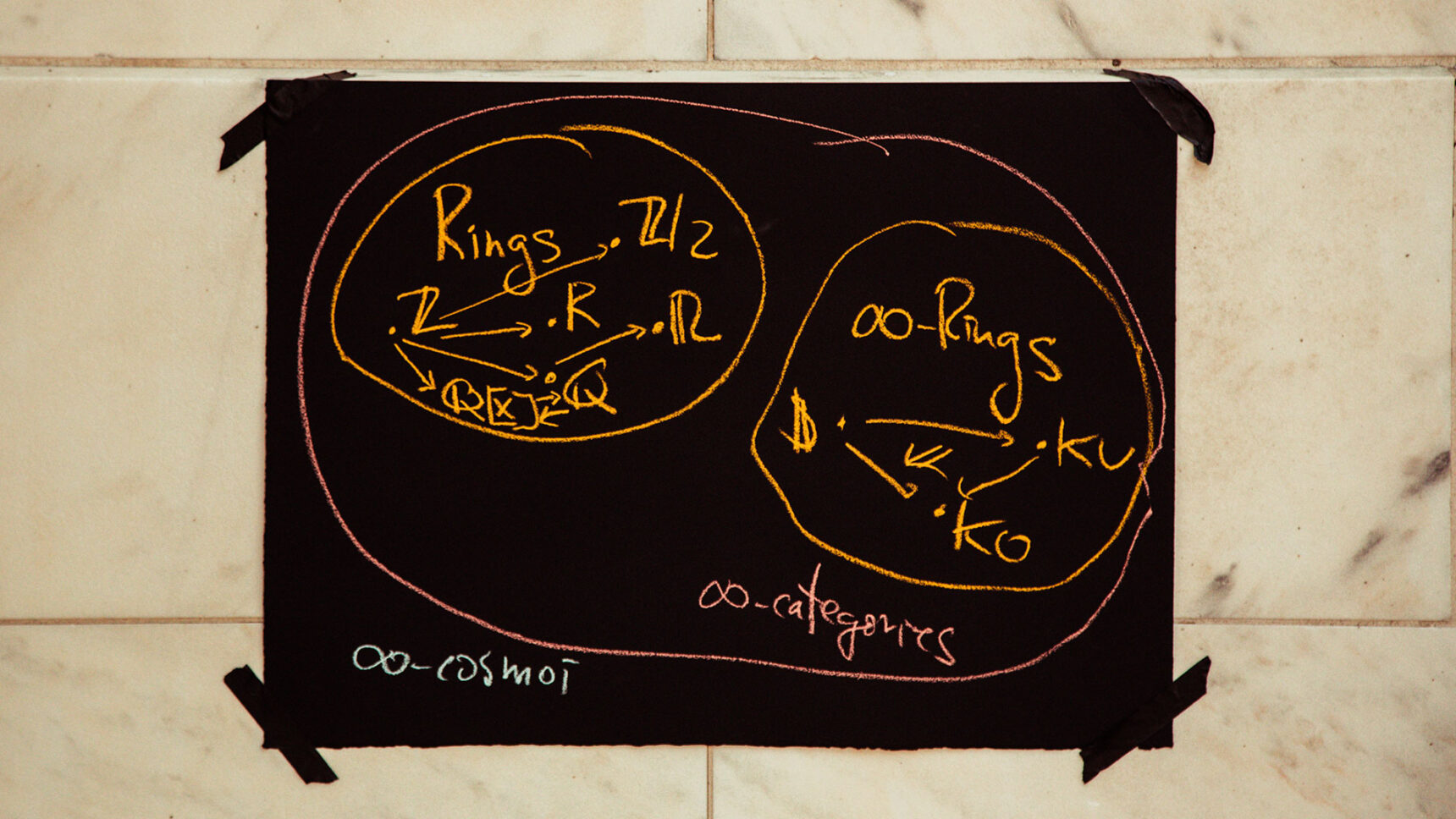
In higher category theory, mathematicians like Riehl don’t just think about ways in which two objects are equivalent. They also think about equivalences between equivalences, and equivalences between equivalences between equivalences, and so on upward in a never-ending tower of relationships. These equivalence relationships are captured in an abstract mathematical object called an infinity category.
Riehl is currently working to expand the usefulness of infinity categories in mathematics. She and her longtime collaborator, Dominic Verity of Macquarie University in Australia, are nearly finished with a book that rewrites the massive, highly technical foundations of the field. Riehl hopes that their reframing will make higher category theory accessible to more mathematicians while offering new insights into why the mathematics of equivalence is so powerful. In part because of this work, Riehl was recently announced as the winner of the 2021 AWM-Joan and Joseph Birman Research Prize in Topology and Geometry.
Quanta Magazine recently spoke with Riehl about her forthcoming book as well as her years playing high-level Australian rules football, how her identity as a queer woman has been “protective” in mathematics, and the obligation mathematicians have to address the social justice issues of the moment. This interview is based on phone and email interviews and has been condensed and edited for clarity.

Riehl on the campus of Johns Hopkins University where she is associate professor of mathematics.
Schaun Champion for Quanta Magazine
You mentioned in another interview that you’ve known you wanted to be a mathematician since you “knew that that was a thing that somebody could be.” When was that?
I think the first time I heard of mathematician as a career option was in Jurassic Park. Jeff Goldblum’s character was obviously the only one who took the threat of the dinosaurs seriously and he was a mathematician. I was 9.
How did it feel to have a career plan at such a young age?
It was very helpful. I was also a musician growing up. I played viola. I knew that the kids who practiced the most were the best. It was just very clear, this correlation between effort and outcome. I knew from a pretty young age that if I could find something that I was passionate about, it would give me a chance to really develop an expertise.
What drew you to category theory?
When I was an undergraduate I was really attracted to abstract algebra. I found the proofs really satisfying. If you’re proving something that relies on some sort of geometric intuition or visualization, I never felt sure that I had it 100% correct. I had the sense that the abstract things are somehow clearer to me than the more concrete things, because I was just more confident that I was understanding them correctly. Category theory is like that to the nth degree.
What is the difference between equivalence and equality, and what’s gained by thinking about equivalence?
Over time, mathematicians have developed an increasingly flexible view of what it means for two objects to be “the same.” In a sense, this progression is inevitable as mathematical objects become increasingly sophisticated. Two objects in a higher category should be considered “the same” when they are equivalent. This essentially means “seen as the same by all other objects in the higher category.” What’s subtle is that an equivalence between two objects should be recorded as additional data.
You’ve compared the role of a category theorist to the role of a violist in an orchestra. In what way are they similar?
If you just had a cello and violin, those are both very pretty instruments, but the sound is not filled out in the way it is when you add a viola, a kind of midlevel harmony. I really think that is how category theory functions in a lot of mathematics.
You have a forthcoming book, Elements of ∞-Category Theory, that you hope will be kind of the new standard text for the field. What inspired the book?
This book describes results from something like 10 papers that I’ve written together with Dominic Verity starting in 2012. We’ve been developing a new approach to the foundations of infinity category theory. Those foundations were developed already by André Joyal and independently by Jacob Lurie. But they’re increasingly central to certain areas of mathematics, and so a lot of mathematicians are trying to learn these topics, but it’s not easy going and depends in a kind of unfortunate way on the choice of a specific model of an infinity category.
And how does your book make higher category theory easier to use?
What Dom and I have hit upon is a way to do everything from scratch that lets you start off working model-independently. So, thinking about infinity categories more abstractly, rather than more concretely. And so now we feel like our perspective is mature enough that we want to rewrite the theorems that we’ve published in various papers in a more accessible form directed at somebody who’s learning this stuff for the very first time.
The specific, more concrete model for infinity categories originated in large part with Jacob Lurie’s massive foundational works from a decade or more ago. Is it fair to call your work a user-friendly rewriting of Lurie?
Part of what we’re trying to do is give a user-friendly rewrite of Lurie. The theorems are the same, the proofs are very different. There are some new insights and, frankly, I think that the new proofs are better.
Why do you think Lurie didn’t use this model-independent framework himself?
I’m not sure whether Lurie realized that it was possible to give rigorous model-independent proofs laying the foundations of infinity category theory. Part of the reason that Dom and I are able to establish something along the lines that I suspect Lurie would have wanted is that we were coming along later. There is also a sociological component to the history. Lurie was forced by the community to choose a specific model to prove theorems about infinity categories, because the ideas were so new, and people didn’t believe the proofs otherwise.

Higher category theory keeps track of an infinite tower of equivalences between mathematical objects.
Schaun Champion for Quanta Magazine
In mathematics, the glory tends to go to people who prove new theorems. There’s less currency in improving known results. How do you think about that with respect to your book?
I’ve sometimes thought of myself as a categorical consultant. One of the things that give me the greatest satisfaction when I think about my career is, it’s not so much about the theorems that I’ve proven, but I think I am playing a supporting role in the mathematical community that is valuable to people.
Bill Thurston had this famous MathOverflow post where he responds to, I think it was an undergraduate, who was concerned that they might not be able to contribute to mathematics, because they weren’t sure how they stacked up to Gauss and Euler and Grothendieck. Thurston reminded this person that mathematics really is a community endeavor and there’s a part to be played by everyone.
It sounds like the same kind of satisfaction that comes with playing the viola.
Nobody would choose to play viola for the glory. But you choose to play the viola because you want to be in an orchestra and you kind of feel like you’re right in the middle of the orchestra a lot of the time. If there’s a big swell, the dramatic ending of The Firebird, you know, you’re right in the middle of it.
Switching topics to another field in which you’ve excelled, you played Australian rules football at a high level, even playing for the U.S. women’s national team.
Yes, it was a huge part of my life for seven years.
But you don’t play anymore?
Well, frankly, what ruined me is, in 2017, I went on sabbatical to Sydney. I was there for eight months and got to play a full season with a proper Australian team. It was really, really wonderful. I was on the best team in Sydney. When I came back, I just knew that it would feel a bit like a letdown after having had the chance to play in Australia for a full season. So, apologies to my U.S. teammates. That was the real reason. I felt like it was time to move on.
You and Mike Shulman are working on a project to translate higher category theory into the language of homotopy type theory. You’ve said you hope this work will make it possible to teach infinity categories to undergrads 100 years from now. Why is that the dream?
Mathematicians feel that they haven’t really understood something until it seems simple. So part of the dream for my field is that someday the community will understand it well enough that we can explain it to undergraduates. That’s a proxy for simplicity.
In your response to the Birman Prize announcement, you thanked the Women in Topology network. Why is that network important to you?
In my experience, the proportion of female mathematicians varies wildly by subfield, and in algebraic topology I can see exactly why it’s such a welcoming area for young women. It has a lot to do with very specific, proactive efforts taken by the generation of women above me who launched the Women in Topology network. They deserve a lot of credit for everything that feels good about algebraic topology today.
Why did you co-found an association for LGBT mathematicians called Spectra?
Prior to Spectra, there wasn’t really a visible, online association for queer mathematicians. So one of the things we have at Spectra that I think is most powerful is the “outlist,” where essentially you just volunteer your name, your position and your institution and you can indicate that you identify as a member of the LGBTQ community in mathematics. The intention with this public list is that a Ph.D. student or a postdoc or somebody who wants to know how comfortable they would feel in a particular city or at a particular institution could get in touch with you.
Have you ever experienced discrimination as a queer mathematician?
No, absolutely not. And I think actually it’s been protective for me in many ways. I think there’s more stigma attached to femininity in mathematics than femaleness necessarily. As a semi-androgynous queer woman, I think that I kind of fit in in the mathematics community better than I would if I were a cis, straight female. I think it also means I’m less likely to get hit on, which is a horrible thing that has happened to a lot of young women in fields where there aren’t enough women.
Spectra came out with a statement in support of Black Lives Matter. You, along with more than 1,500 other mathematicians, also signed a pledge to boycott working with police departments. Why was it important for you to sign that letter?
I’m concerned. We’ve definitely had issues with corruption and abuse in the police department in Baltimore. And at Johns Hopkins, there’s this controversy surrounding a proposal by the administration to introduce a private police force on campus. We’re in a situation where Baltimore is a majority Black city, whereas the majority of people on Johns Hopkins’ campus are not Black. That makes me very concerned for Black students on campus, including one of my Ph.D. students.
What role or responsibility do you feel that mathematicians have to address social issues of the moment?
I think it’s very important that we do as much as we can to make sure that all our students have an equal opportunity to learn. If your class has one Black Indigenous person of color and no one else who looks like them, and everyone else is in a study group and this one individual is not, that’s a huge problem.
It’s also a problem if as an instructor you’re using language that suggests that certain arguments are trivial or that this is something that everybody learned in kindergarten. These are tropes that mathematicians like to use, and I think they’re very alienating to people who, for one reason or other, did not learn about modular arithmetic in kindergarten. We have to figure out ways to be allies and mentors for people who are not having the same experiences that we did.