First Map Made of a Solid’s Secret Quantum Geometry

The possible quantum states of a crystal carve out a curved shape.
Mark Belan/Quanta Magazine
Introduction
Famously, at the quantum scale, particles can be in multiple possible locations at once. A particle’s state spreads out like a wave, peaking where the particle is likely to be found. When you measure its position, this spread-out state, known as a wave function, transforms into a single definite location.
The full shape of the wave function long evaded detection, since trying to measure it will destroy it. But in the 1980s, physicists began developing methods to measure and control the wave functions of simple systems — advances that have since formed the foundation of quantum computing. And in the last few years, a new approach is enabling physicists to go further and learn about the wave functions of entire materials.
“We are in the second quantum revolution,” said Riccardo Comin, an experimental physicist at the Massachusetts Institute of Technology who is one of the leaders of this work. “Now, we have the tools to really explore the wave function of quantum particles.”
The new framework describes a wave function as an object moving around a hidden landscape — a space referred to as the material’s “quantum geometry.” The hills and valleys of this invisible world dictate how the wave function of a given material can change, and what states the material can be found in.
“You can get a lot of insight into what’s happening in quantum materials, and that may speed up the discovery of new phenomena,” said Marc Bockrath, a physicist at Ohio State University who has also led the charge on quantum geometry.
Comin and collaborators recently measured the full quantum geometry of a crystal — a first peek into the wave function of a real material.
Let’s explore the hidden landscapes that are coming into view.
Secret Geometry
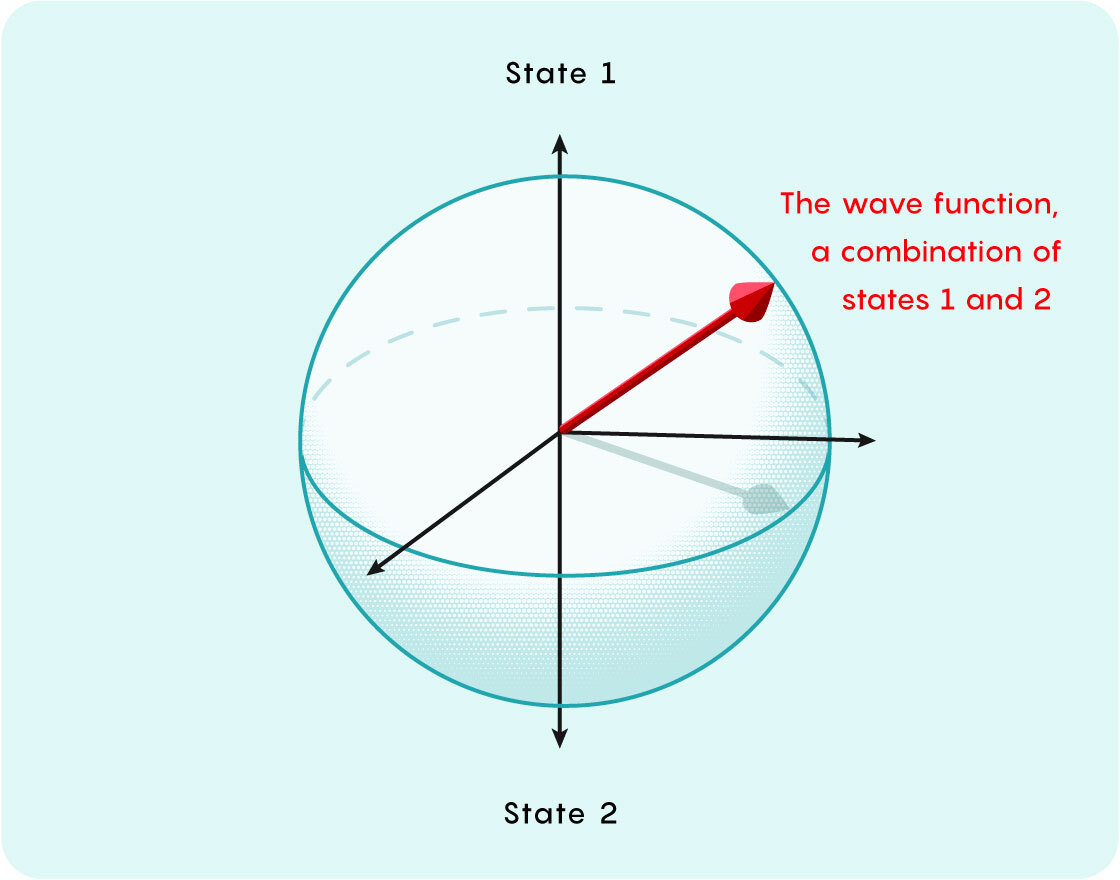
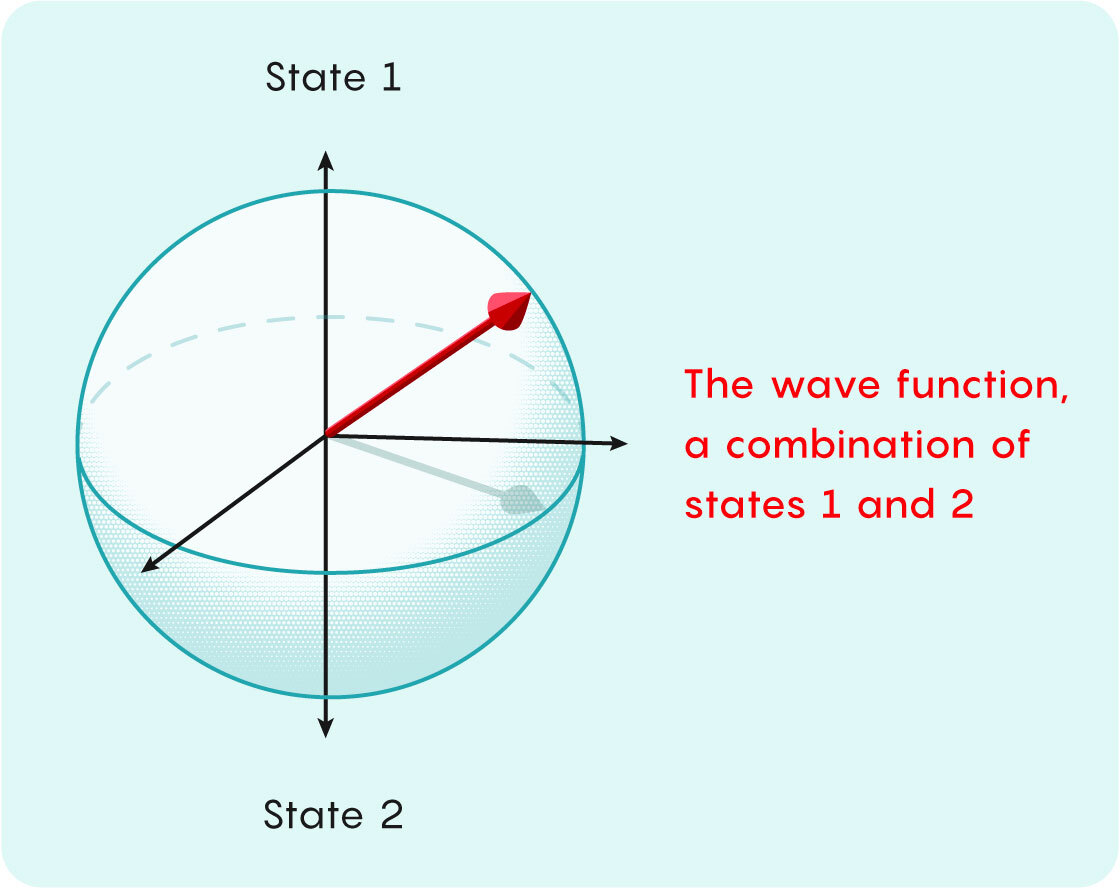
Physicists often think of a particle’s wave function as an arrow. If the particle can be found in two possible states, they represent these options as opposite directions for the arrow to point in — say, up and down. If the particle is in a combination of both states, then the arrow points somewhere around a sphere, with the two states corresponding to the poles.
Mark Belan/Quanta Magazine
The arrow’s direction captures the relative likelihood of each possibility. Measuring the particle will snap the arrow into pointing exactly up or down, and the chance of each outcome depends on which pole it’s closest to.
Many particles have more than two possible states, in which case the arrow occupies a high-dimensional space. That’s impossible to visualize, but the math gives physicists a sense of the particle’s wave function at a given moment.
For materials made of many particles, a single high-dimensional arrow can represent the combined state of all the electrons inside it. This collective arrow will swing around as you change the material’s ambient conditions — its temperature, for example, or the strength of the magnetic field around it. To control a material, physicists need to know how the arrow will rotate as they turn these various knobs.
To keep track, they build a map. Imagine, for example, that you change the strength of the magnetic field that you apply to the material. On your map, you’ll make the east-west direction correspond to that magnetic field strength. When the field is weak (corresponding to west on the map), the wave function of your electrons will be in some state, which you can represent with an arrow. With stronger magnetic fields, you’re farther east, and the wave function assumes a different state. As you move from west to east across your map, the arrow will rotate, showing how the wave function of the electrons changes as you dial the field up or down.
This map can be expanded to capture every way you can adjust a material. Each adjustable knob, or parameter, adds a new dimension you can move in on the map.
Imagine tracking how quickly the arrow rotates as you move across this map. With that information, the map becomes 3D, as though you’re mapping a mountain range. The steeper the landscape at each part of the map, the more the electrons’ wave function will change around those values of the parameters. If it changes a lot, you’re on a mountain. If it doesn’t change at all, you’re on flat ground.
A mathematical object called the quantum metric captures the shape of this landscape. It does this by describing the path with the shortest distance between two points. Just as a plane flying from New York to Beijing won’t cut through the Earth but will instead curve over the Earth’s surface, the path between two quantum states reveals the underlying geometry they exist in.
This secret geometry of wave functions went undetected for decades. But when quantum materials began to surprise physicists with inexplicable behaviors, physicists in the 1980s realized that some of the behaviors could be explained by a material’s wave function traveling around a curved shape.
Imagine an arrow moving around a flat plane. Its direction won’t change. But on a curved surface, after traveling in a closed loop, the arrow will point in a different direction than it did when it started.
The same thing can happen with quantum states. Imagine varying the conditions of a material to move the wave function around the map, then bringing the material back to its initial conditions. If its arrow now points in a new direction, the material is “topological”: Its hidden, underlying shape has forced the material into a new state.
The change in direction caused by the underlying topology is called the Berry phase, after the British theoretical physicist Michael Berry, who popularized the idea. The way this phase accumulates over a looping path is called the Berry curvature, referencing the curved shape that the arrow is secretly traversing.
To Comin, the Berry phase is “one of the most fascinating concepts in the quantum theory of solids.” Though long invisible to experimenters, the Berry phase can have bizarre physical consequences.
Sprinkled Doughnuts
This abstract geometry comes to life in laboratories where physicists like Comin study crystals — lattices of atoms in repeating patterns. In recent years, they’ve found that 2D crystals — flat lattices of atoms in which electrons can move in two directions — host a wild variety of quantum behaviors. Let’s see why the map of a 2D crystal’s quantum geometry takes a doughnutlike shape called a torus.
In general, the repeating patterns in crystals limit the possible states of the electrons inside them. The electrons can flow quickly or slowly, or not at all, and each option corresponds to a different collective wave function. For a 2D crystal, physicists can fit the map of possible states on a piece of paper: Each coordinate corresponds to the possible momentum of electrons in the vertical and horizontal directions.
Since the map of states of a crystal repeats, traveling in one direction off the edge of the flat map brings you back around to the other side. To show this, physicists take the map and wrap it up twice. First the flat map becomes a cylinder, and then the ends of the cylinder meet, creating a torus.
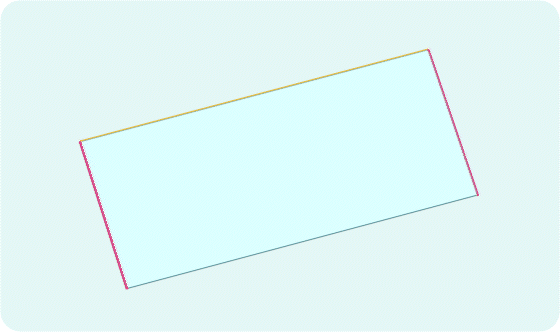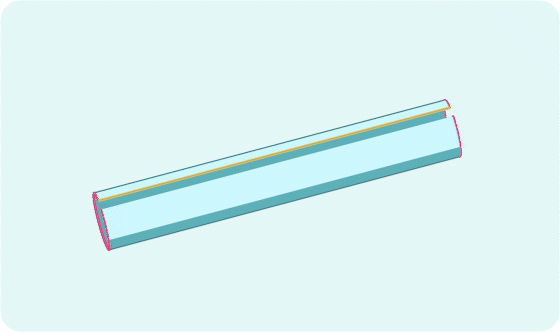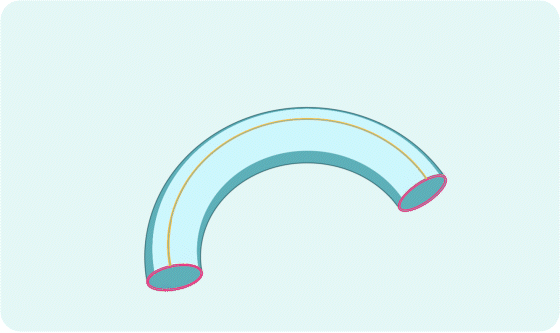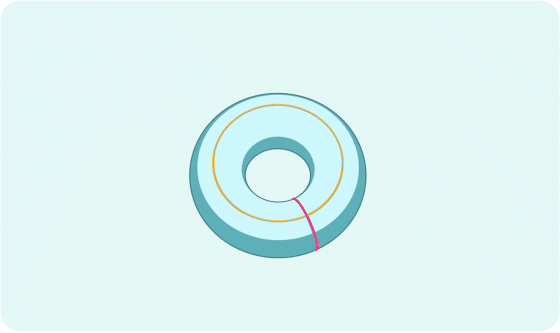
Changing the conditions, such as by running a current through the crystal, will change the motion of the electrons, which will push the arrow around on this torus-shaped map.
And with topological materials in particular, dialing the knobs and then returning to the initial conditions — in other words, tracing a looping path around the torus — leaves the electrons’ arrow pointing in a different direction from before. This means that multiple arrows, or wave functions, can coexist at the same point on the torus, creating a “point of discontinuity.”
As the electrons pass over such a point, their collective arrow suddenly flips, and the material’s state drastically changes.
This effect is similar to that of passing over an electric charge, which would likewise flip the force on the electrons. For this reason, topological materials can be interpreted as hosting ghostly charges, which cause electrons to move as if they feel a force field that doesn’t really exist.
The discovery of this “ghost field” in the 1980s cemented the connection between the hidden geometry of quantum states and the behavior of materials. It was part of the work that won the 2016 Nobel Prize in Physics.
Uncharted Territory
Topological materials are no longer so mysterious: Physicists commonly use them to discover new phases of matter and are exploring their potential for quantum computing. But only recently have they come to appreciate the fuller picture of quantum geometry that includes not only the Berry curvature but also the quantum metric — the shape of the rugged landscape that can exist on top of a torus-shaped map. A couple of years ago, the quantum metric helped researchers understand what was going on in a 2D crystal that hosted an exotic new form of superconductivity — the flow of electricity with no resistance.

The physicist Riccardo Comin (top) and collaborators recently mapped the full quantum geometry of a crystal for the first time. Päivi Törmä (bottom) helped show how quantum geometry can explain exotic material behaviors such as superconductivity.

The physicist Riccardo Comin (left) and collaborators recently mapped the full quantum geometry of a crystal for the first time. Päivi Törmä (right) helped show how quantum geometry can explain exotic material behaviors such as superconductivity.
Courtesy of the MIT Research Laboratory of Electronics; Mikko Raskinen/Aalto University
The results suggested that the quantum metric may be a powerful framework for understanding materials. Some see it as opening a door to someday engineering room-temperature superconductors, which, if achieved, could transform everything from quantum computing to solar energy. “We can start to search for the same mechanism” in other materials, said Päivi Törmä, a physicist at Aalto University in Finland who helped explain the exotic superconductivity in terms of the quantum metric, “and that can be very promising.”
Motivated by those developments, Comin and Mingu Kang, a physicist at Seoul National University, have taken the first-ever snapshot of the quantum geometry of a crystal.
Physicists have long studied crystals by hitting them with ultraviolet rays to knock out electrons. By measuring the energies of the shed electrons, they can see how well the material conducts electricity and determine whether it’s an insulator, a metal or something in between.
Comin and Kang gave the classic method an upgrade. They worked with a topological crystal called a kagome solid, which has layers of atoms arranged in a six-sided starlike pattern. They wanted to see the effect of the topological “ghost field” on the crystal’s electrons so that they could measure its Berry curvature — one part of its quantum geometry.
They hit the crystal with circularly polarized light, then measured the energies of electrons of each spin direction. The ghost field imparted an extra force on the electrons in different directions depending on their spin. From this, they could extract the Berry curvature.
Then Comin teamed up with Bohm-Jung Yang’s group in Seoul in a joint effort to probe the quantum metric of the kagome solid. “No one had done this before in a solid,” Comin said. “It was completely unprecedented.”
The key was to measure both the electrons’ energies and their velocities and see how the two quantities relate. The different velocities map onto different points on the torus, so these measurements gave the approximate curvature captured by the quantum metric.
Together, the measurements painted a picture of the crystal’s entire quantum geometry. “Looking at these two independent measurements, we showed that they basically beautifully match,” Comin said. “We’re starting to see the geometry of these states. And that’s something I’ve never seen before in my life.”
Their method can be used on many kinds of crystals. In a new paper in Science this week, Yang’s team applied the same approach to a crystal called black phosphorus. Some think it could become a ubiquitous way to study quantum materials.
Quantum geometry “will certainly become a standard tool or way of seeing things,” Törmä said. “But how much is revealed by it? That remains to be seen.”



