Banach-Tarski and the Paradox of Infinite Cloning

Imagine two friends hiking in the woods. They grow hungry and decide to split an apple, but half an apple feels meager. Then one of them remembers one of the strangest ideas she’s ever encountered. It’s a mathematical theorem involving infinity that makes it possible, at least in principle, to turn one apple into two.

That argument is called the Banach-Tarski paradox, after the mathematicians Stefan Banach and Alfred Tarski, who devised it in 1924. It proves that according to the fundamental rules of mathematics, it’s possible to split a solid three-dimensional ball into pieces that recombine to form two identical copies of the original. Two apples out of one.

“Right away, one sees that it’s completely counterintuitive,” said Dima Sinapova of the University of Illinois, Chicago.

The paradox arises from one of the most mind-bending concepts in math: infinity.

Infinity feels like a number, yet it doesn’t behave like one. You can add or subtract any finite number to infinity and the result is still the same infinity you started with. But that doesn’t mean all infinities are created equal.

Over the past century, mathematicians have proved that some are bigger than others. For example, the natural numbers (1, 2, 3, and so on) are a countable infinity. They go on forever, but it’s possible to count them off (like listing the numbers 1 through 1 trillion).

By contrast, the real numbers — all the infinitely many tick marks that denote decimals on the number line — are an uncountable infinity: It’s impossible to count all the real numbers that lie on any interval on the number line, even a seemingly very small one, like the interval between zero and 1.

This difference between countable and uncountable infinities makes the natural numbers a smaller infinity than the real numbers — a distinction that mathematicians convey by saying the two have different “cardinality.”

Distinguishing cardinalities is more than conceptual jiujitsu — in 1891 Georg Cantor proved that there really are more real numbers than natural numbers. Cantor also proved that the infinite number of points on a line has the same cardinality as the infinite number of points that fill the volume of a shape, like a sphere.

Banach and Tarski realized you can turn one sphere into two by partitioning the uncountably infinite set of points it contains into — get ready for it — an uncountably infinite number of countably infinite sets. The separation occurs through a very specific dissection procedure.

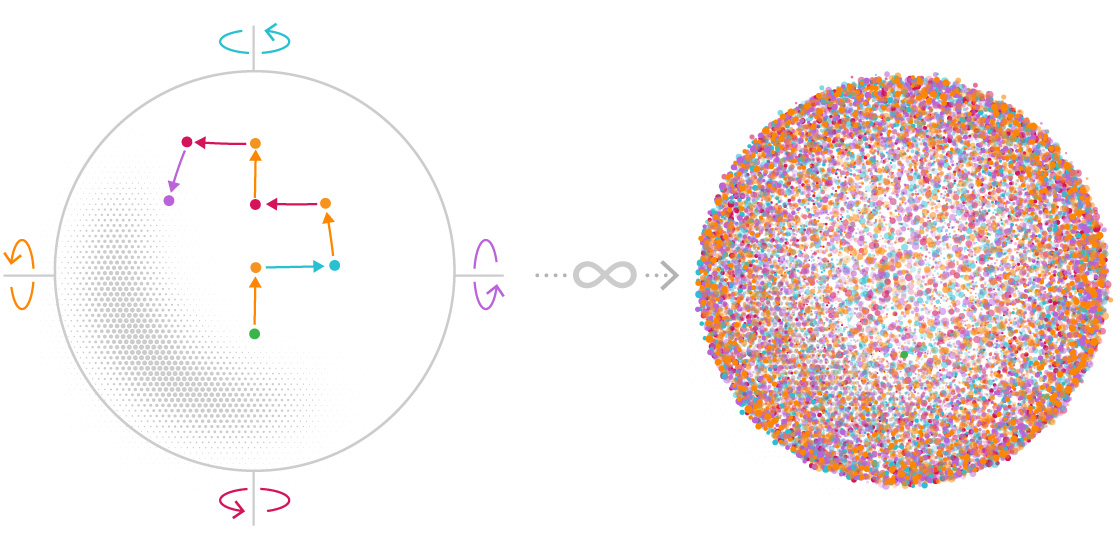
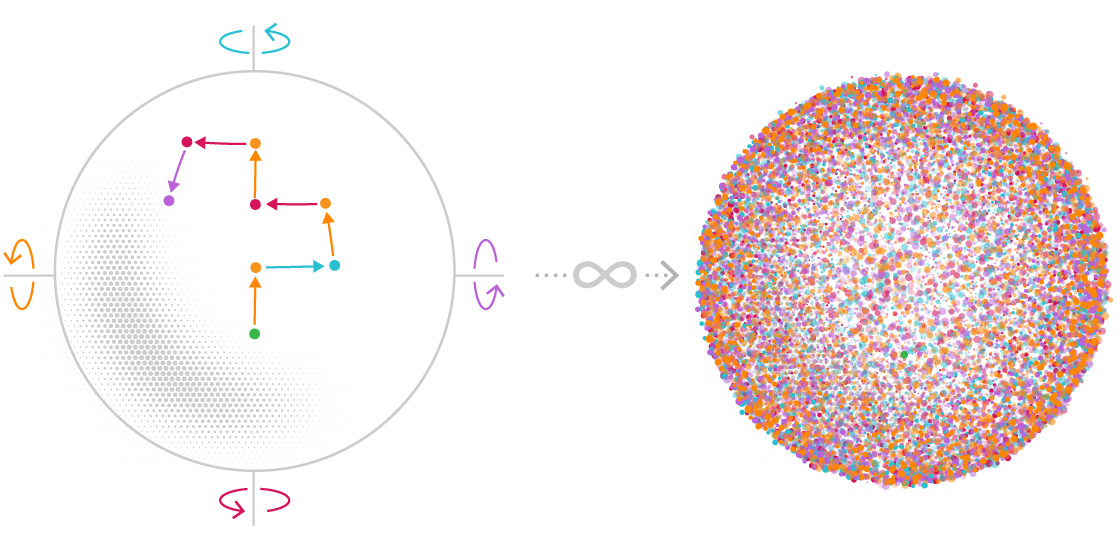
To build one of these countably infinite sets, pick a starting point. Any point in the sphere will do. Next, choose two angle measurements that are an irrational number of degrees (that is, any number of degrees, like pi, that can’t be written as a fraction). In a moment you’ll start rotating the sphere. One of these angles is for North-South rotations and the other is for East-West rotations.

Now, rotate the sphere North, South, East or West by the appropriate number of degrees. You’ll land on a new point. This is the second point in your set (the first point is your starting point).

Then, rotate the sphere again in any of those four directions, with the one stipulation that you can’t directly backtrack in the direction you came from — no rotating West just after you rotated East. You’ll get a third point. If you repeat this procedure an infinite number of times you’ll create a set with infinitely many points.

This set will have a couple of key properties. The first is that it will never include the same point more than once — this is guaranteed by virtue of the fact that your angles of rotation are irrational. The second is that the set will be countably infinite — you could assign a natural number to each point selected through the rotation process.

“The whole sphere is this uncountable object,” said Spencer Unger, a set theorist at the University of Toronto. “But it’s broken up into a bunch of countable pieces.”

Repeat this same procedure starting from any point on the sphere. Each starting point generates its own unique set of subsequent points. In this way, you can create an uncountably infinite number of sets, each of which contains a countably infinite number of points.

Once you have these sets, you’re going to sort their points into a handful of groups. Four groups will be identified by the last rotation performed before landing on a point. A fifth group will contain the center point of the sphere and all the points at the poles. A sixth group will collect every starting point.

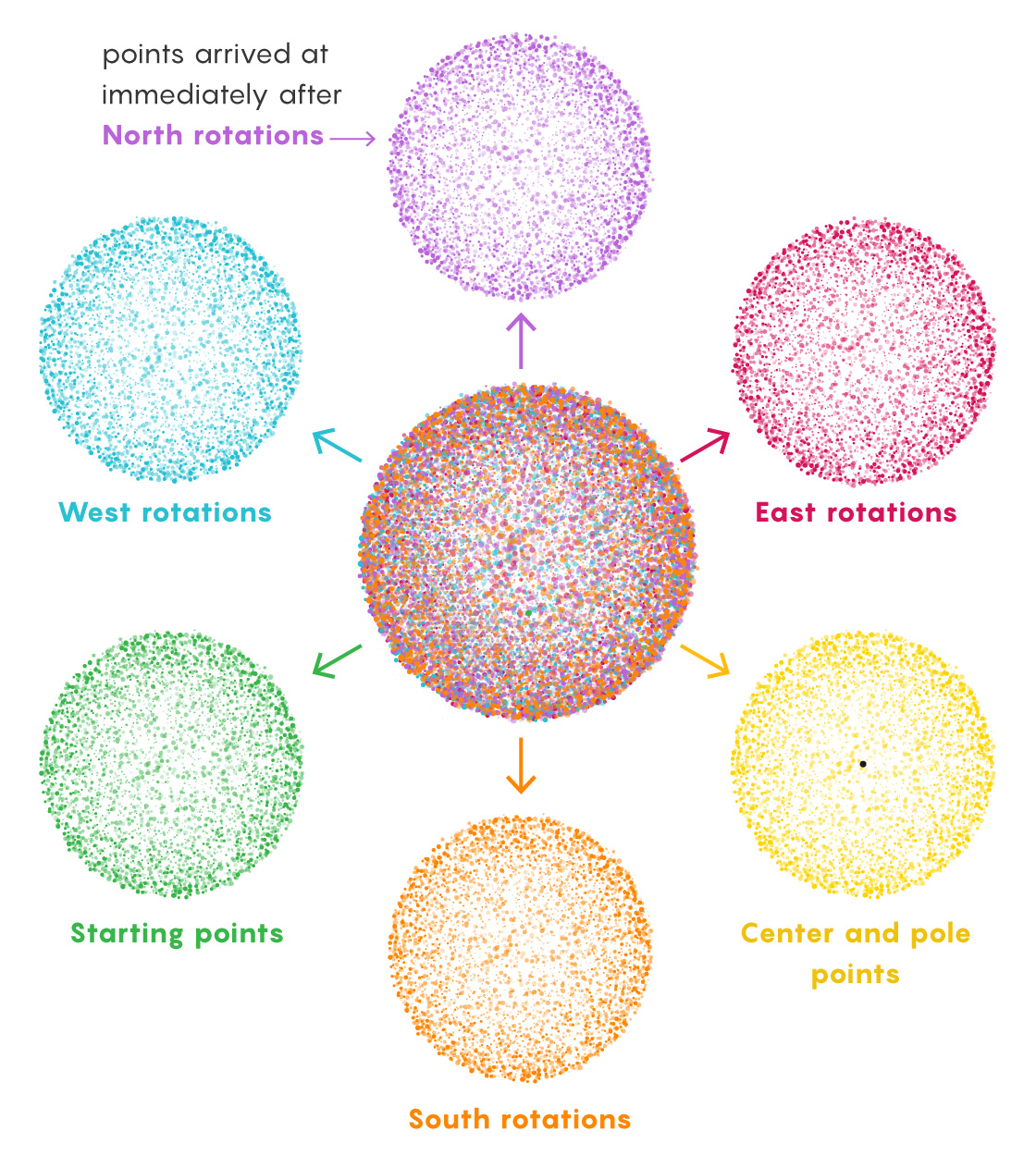
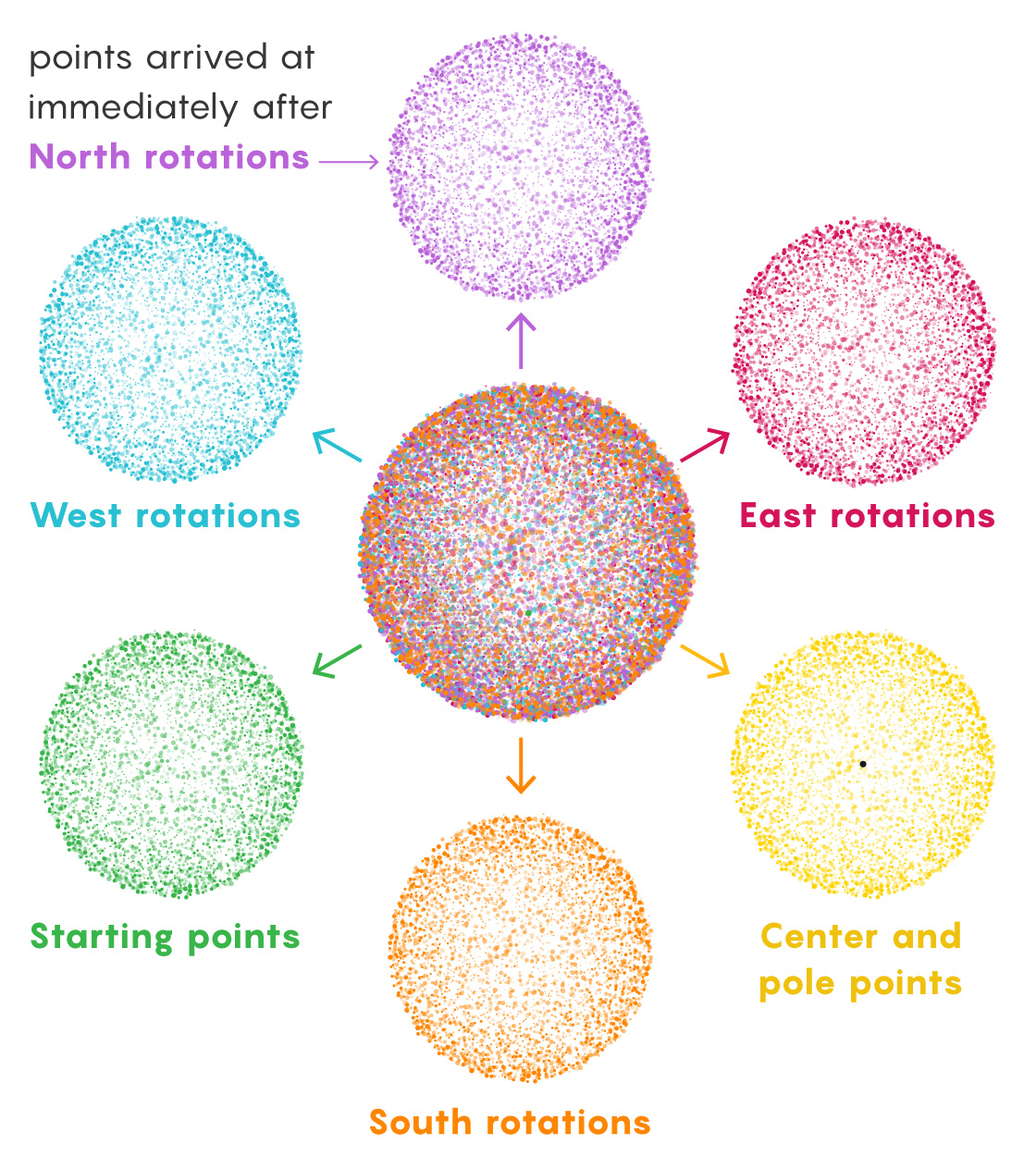
If you were to combine these groups they would still only produce one sphere — not the two Banach and Tarski were after. To double it, they adapted an idea from the mathematician Felix Hausdorff, which allowed them to rotate all the points within a single group to create a different set of points which was larger than the group they started with.

Take, for example, the group that contains all points derived from a final rotation to the East. Now, rotate this group to the West. This instantly negates all those final East rotations and transforms the group into the (still infinite) collection of points that immediately preceded the formation of the original sets during the set-building process. The group now contains points that finished on North, South and, critically, East rotations, which was the original basis for the group. In other words, the rotated piece contains new stuff and its old self.

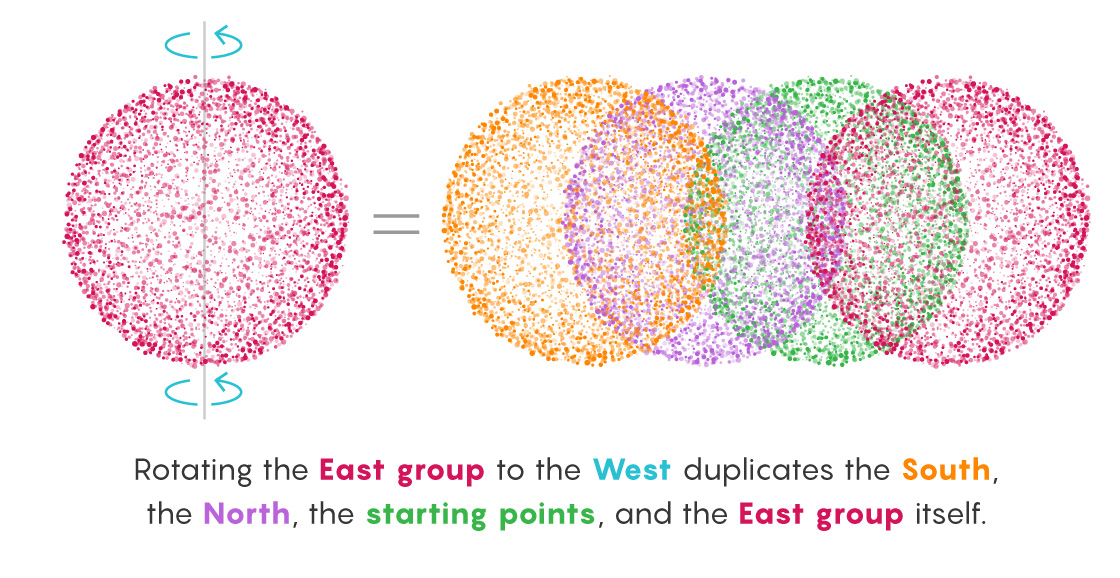
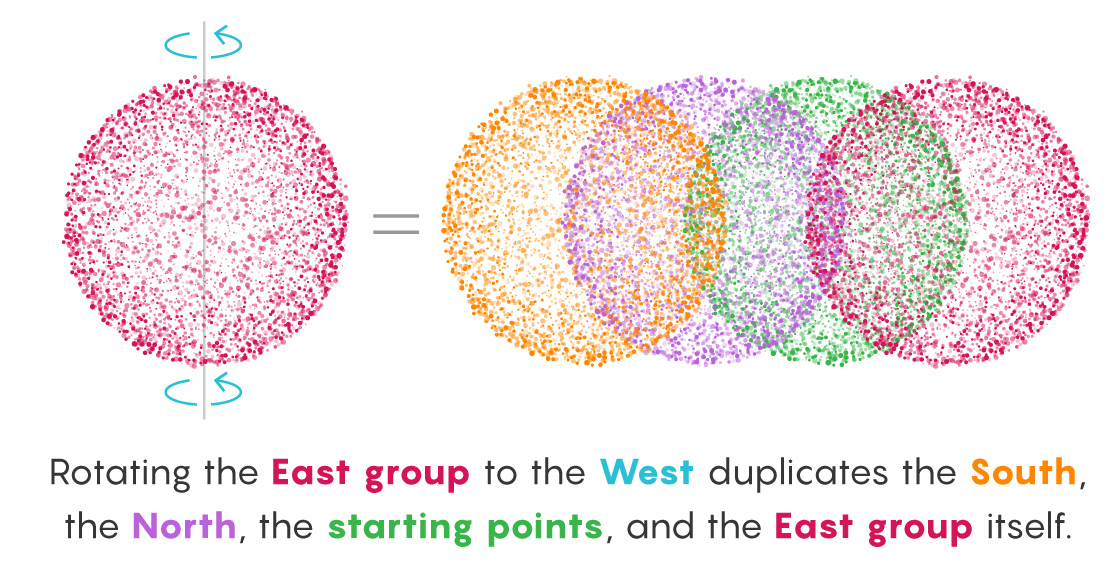
The nature of infinity makes this seeming increase possible. Turning the entire East group West erases all the last East rotations. So what remains?

No West-ending paths preceded the final Easts because backtracking wasn’t allowed. But an infinite number of East-ending paths preceded those final East turns (no rule forbids making East-East your last two rotations). An infinite number of paths ending with Norths and Souths did, too. Merely by rotating the entire East group West, we’ve turned it into a group that contains all East, North and South points. All the starting points are in there now, too (because every path consisting of just one East turn has now returned to its origin).

At this point we’ve duplicated all the points in three of the six groups (North, South and starting points). Next, we just need to duplicate the other three groups (East, West and poles/center). The first two are easy: Just rotate the North group South, which gives you all North, East and West points.

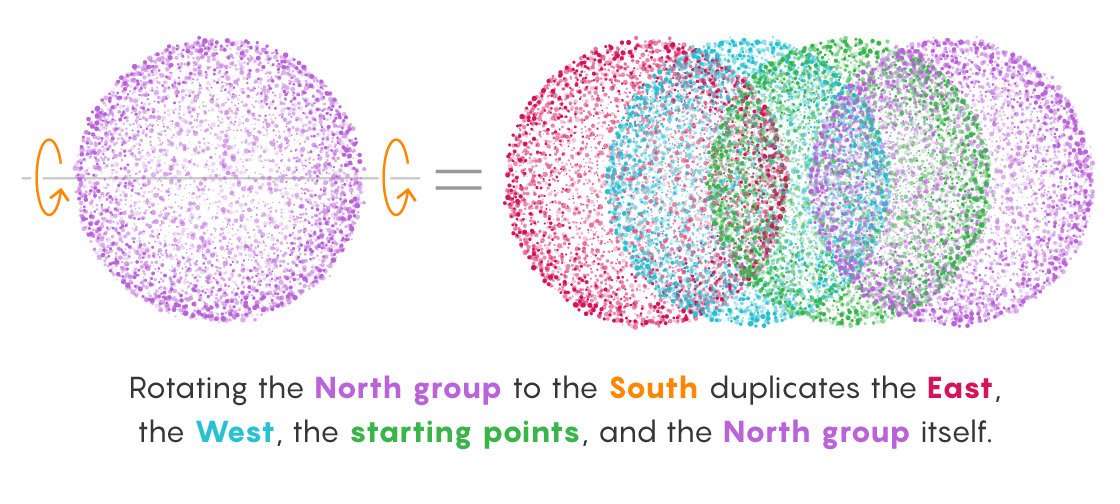
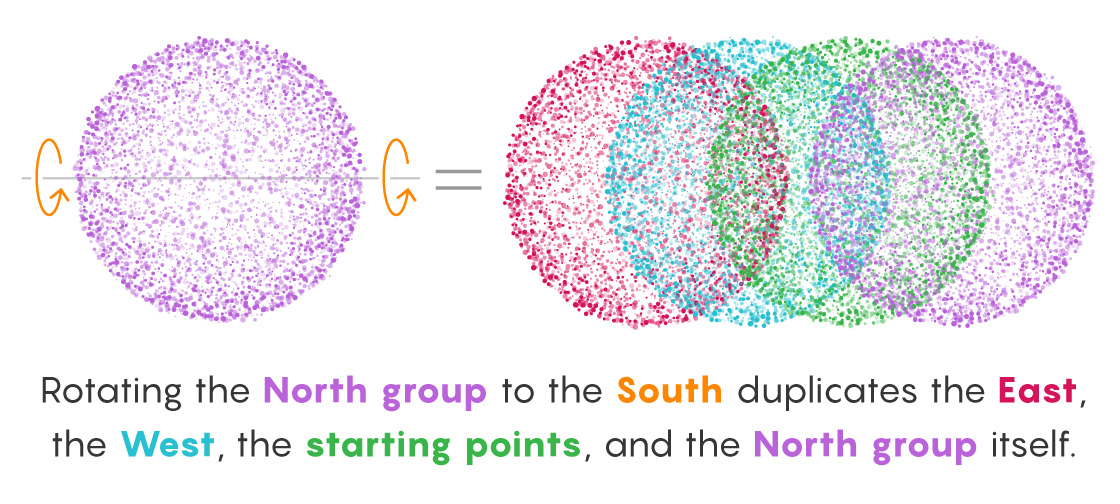
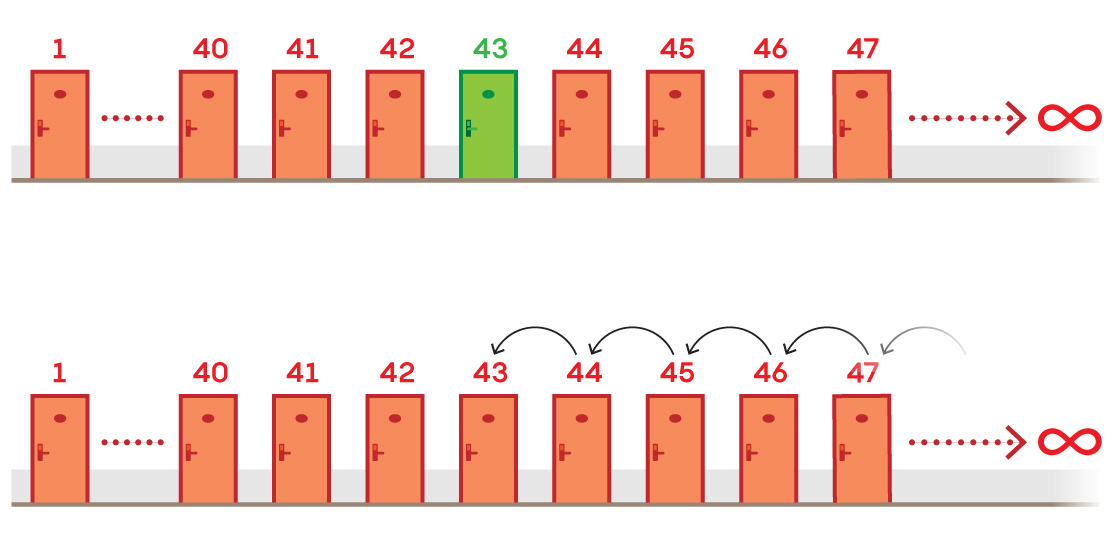
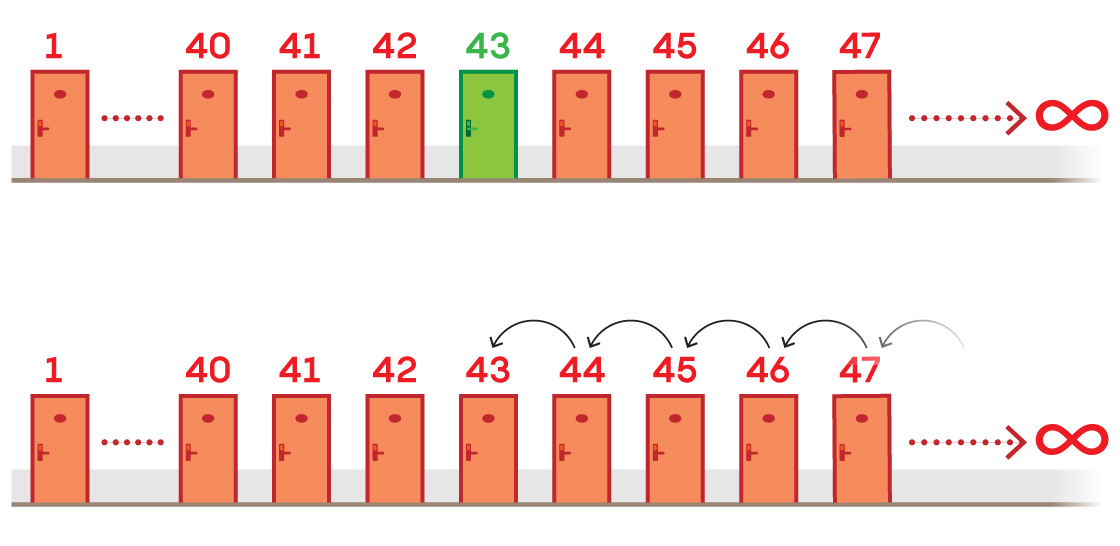
Finally, we need to duplicate the poles and the center point. This occurs through a process similar to that of another infinity-related argument called Hilbert’s hotel, devised by David Hilbert in 1924, the same year Banach and Tarski came up with their paradox.

In this thought experiment, imagine a hotel with an infinite number of rooms. Suppose that only Room 43 is empty. Take every guest in Room 44 and above and move them down one room. You’ve filled the vacancy without creating a new one (because when you shift infinite guests over one room, there’s always a guest to replace the one you just moved).

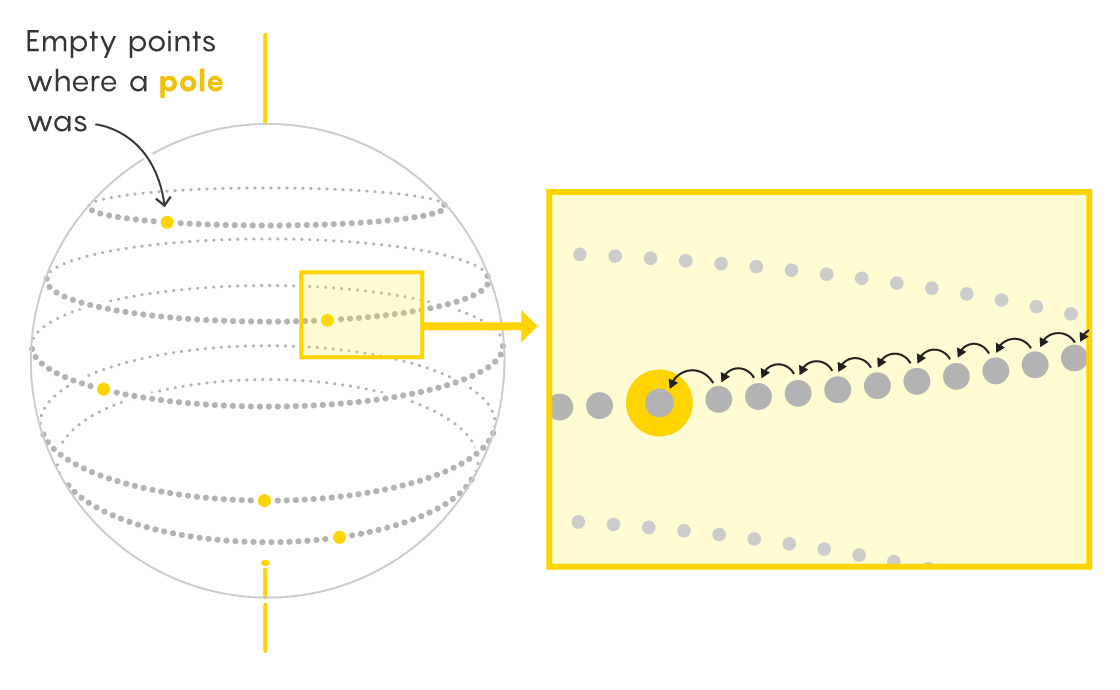
Now imagine the missing set of poles as vacancies dotting different lines of latitude on the duplicate sphere. Shift all the points on each line of latitude over, and infinity fills the vacancies.

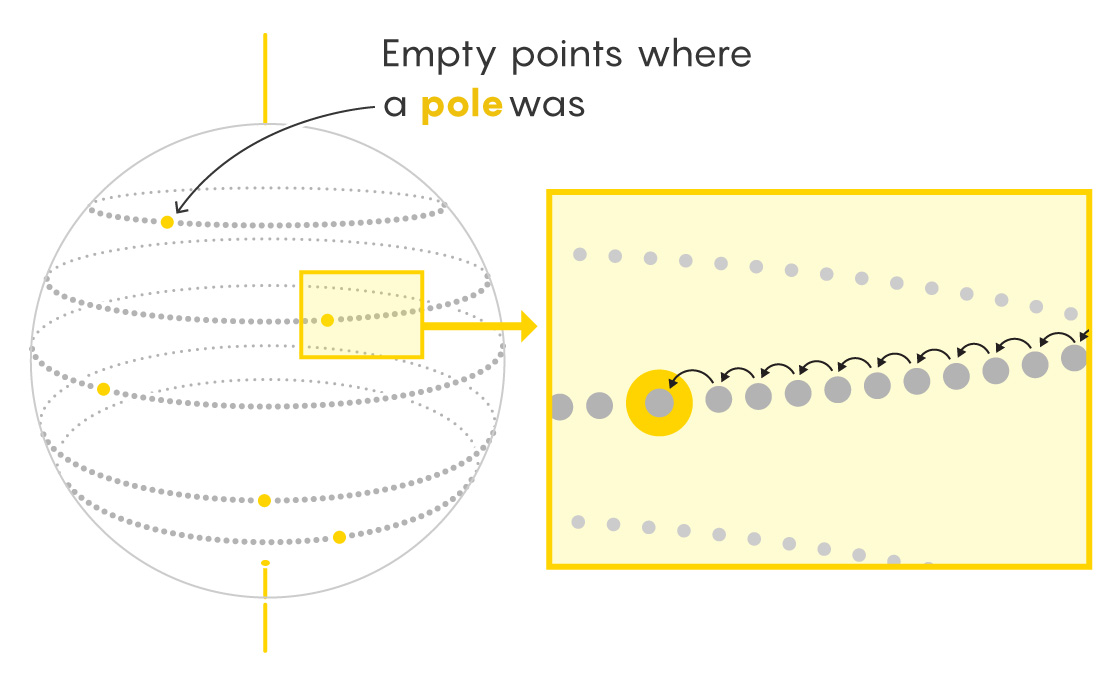
The vacant center point exists on another circle that can be filled the same way. As a result, voila! We’ve duplicated all six groups. We can now combine each set of six groups into its own sphere.

The outcome feels impossible. How can you double the volume of an object just by decomposing and rearranging it? One explanation is that Banach-Tarski offloads the burden of uncountability. Decomposing the sphere with sequential rotations, like counting off natural numbers, creates a more manageable workspace — a more manageable infinity than the uncountable one plaguing the initial sphere.

The paradox has detractors. Some see it as an absurd conclusion that points to a flaw in the rules of mathematical reasoning that enable it.

“It’s like a bellwether,” said Norman Wildberger, a recently retired professor of mathematics at the University of New South Wales in Sydney, Australia. “It’s like a massive red flag.”

The mathematical rule that makes the Banach-Tarski paradox possible is called the axiom of choice. It’s one of nine axioms in a system called Zermelo-Fraenkel set theory, or ZFC, that serves as the foundation of modern mathematics.

In the historical development of ZFC, the axiom of choice is sometimes viewed as an add-on to the other eight — a status that makes it vulnerable to criticism when it enables outcomes like the Banach-Tarski paradox. The axiom of choice grants mathematicians the power to “choose” an item from each bin of a collection, even if that collection is infinite. This makes Banach-Tarski a Rorschach test for working with infinity: Many see the paradox as wondrous; critics like Wildberger cringe.

But most mathematicians don’t lose sleep over the axiom of choice. They see the Banach-Tarski paradox as a demonstration of the richness of mathematics. It offers a law-abiding example of how math can stray from physical intuition without contradicting itself.

“Almost anything can be doubled — can be decomposed into two things of the same cardinality,” said Sinapova.