James O’Brien for Quanta Magazine
Look at a picture of a cat, and you’ll instantly recognize it as a cat. But try to program a computer to recognize cat photos, and you’ll quickly realize that it’s far from straightforward. You’d need to write code to pinpoint the quintessential quality shared by countless cats in photos with distinctive backgrounds and taken from different camera angles. Where would you even begin?
These days, computers can easily recognize photos of cats, but that’s not because a clever programmer discovered a way to isolate the essence of “catness.” Instead, they do it using neural networks, artificial intelligence models that learn to recognize images by looking at millions or billions of examples. Neural networks can also generate text with startling fluency, master complex games and solve problems in math and biology — all without any explicit instruction.
There’s a lot that researchers still don’t understand about the inner workings of neural networks. But they’re not completely inscrutable. By breaking down neural networks into their basic building blocks, we can explore how they learn to tell a tabby from a tablecloth.
A Simple Classifier
Cat detection is an example of what researchers call a classification task. Given an object — in this case, a picture — the goal is to assign it to the right category. Some classification tasks are much simpler than telling “cat” from “not cat.” Let’s consider a fanciful example involving two fictional regions, Triangle Territory and Square State.
You get a new point, described by its longitude and latitude coordinates, and have to decide which region that point lies in. But you don’t have a map that shows the border. Instead, you have only a set of known points in the two regions.
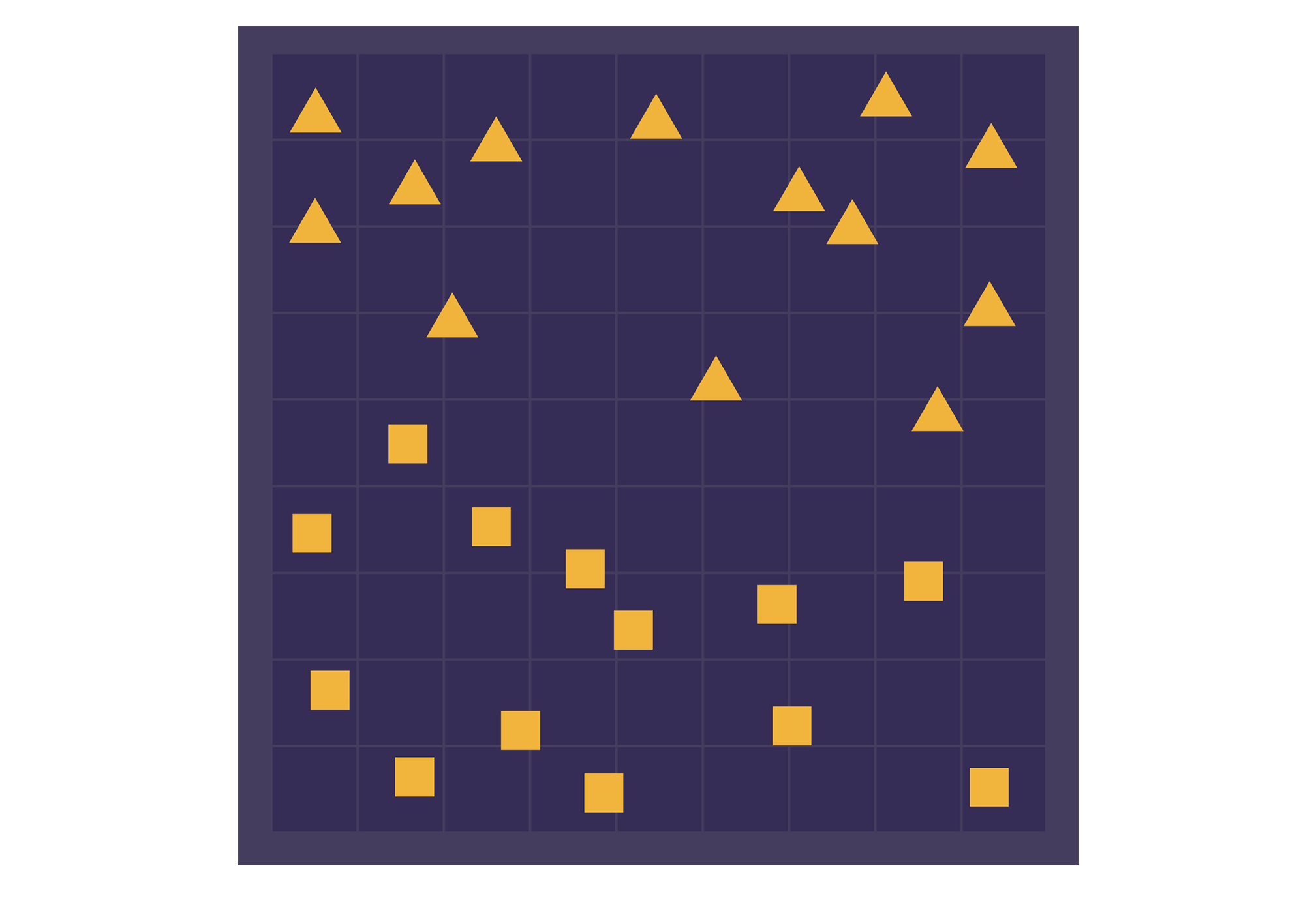
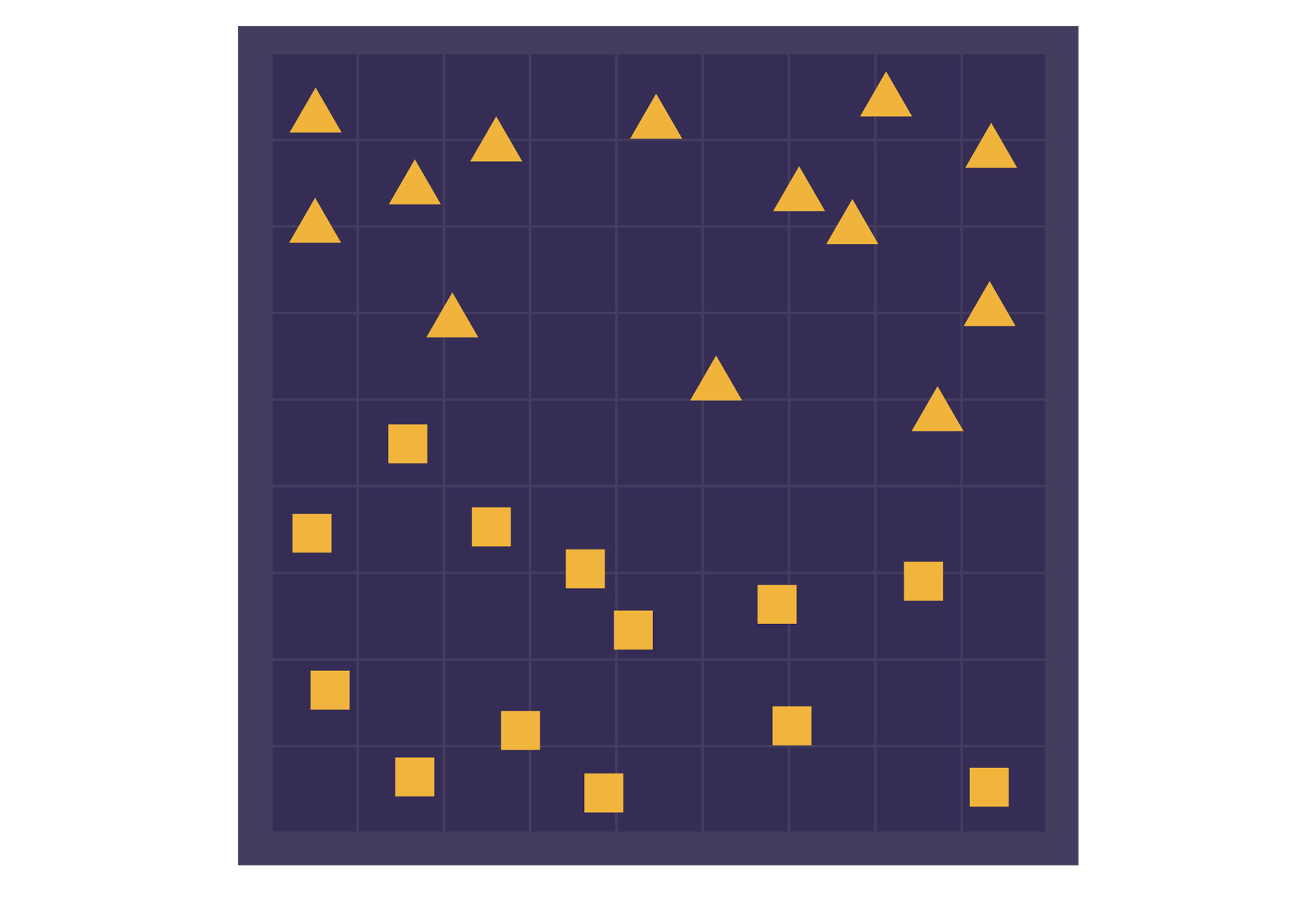
To build a “classifier” system that will automatically categorize unknown points, you need to draw a boundary. After that, when you’re given a new point, the classifier can just look at which side of the boundary it’s on.
But how do you decide where to draw the boundary? That’s where neural networks come in. They find the most likely boundary based on the initial set of known data points.
Before we can understand how that process works, we’ll need to set aside our map and explore the basic building blocks of neural networks, called neurons. A neuron is just a mathematical function, with several inputs and one output. Put in some numbers, and it’ll spit out a new number. That’s it.
Even simpler, the output will almost always be either close to 0 or close to 1. Which will it be? It depends on the inputs as well as another set of numbers, called parameters. A neuron with two inputs has three parameters. Two of them, called weights, determine how much each input affects the output. The third parameter, called the bias, determines the neuron’s overall preference for putting out 0 or 1.
Now let’s take a look at the relationship between inputs and outputs. The three illustrations below show neurons with three different sets of parameters. As the inputs change in each case, they’ll cross a boundary where the neuron’s output rapidly rises from 0 to 1. On these plots, the boundary is always a straight line. The parameters determine the position and angle of that line.
To create a classifier that tells us if a new point should be in Square State or Triangle Territory, we need to adjust this line so that it accurately represents the border between the two regions. Here, we’ll say a point is in Square State if the output is close to 0, and in Triangle Territory if it’s close to 1.
To adjust the line, we need to adjust the neuron’s parameters through a process called training. The first step is to set the parameters to random values, which means the neuron’s initial boundary line won’t look anything like the actual border.
During training, we feed the longitude and latitude of each known data point into the neuron’s inputs. The neuron will spit out an output based on its current parameters, then compare that output to the true value. Sometimes, it’ll get the right answer.
Other points will be classified incorrectly.
Whenever the neuron gets the wrong answer, an automated algorithm tweaks the neuron’s parameters slightly, in a direction that moves the boundary closer to the incorrect point.
The algorithm repeats this process many times as it churns through the training data. Eventually we’ll end up with parameter values corresponding to the straight line that best approximates the true shape of the border.
Finally, we’re ready to use the classifier on new data that wasn’t used for training. It’s not perfect, but it’ll get the right answer most of the time.
A Network of Neurons
A single neuron works pretty well for our simple example, but only because the true border between Triangle Territory and Square State was close to a straight line. For harder tasks, we’ll need to use a collection of many interconnected neurons — a neural network. Like an individual neuron, a network is just a mathematical function. Numbers go in, and other numbers come out.
The neurons inside a neural network are arranged in groups called layers.
A layer can contain any number of neurons, and networks can have any number of layers. The outputs of the neurons in each layer become inputs to the neurons in the next layer.
Large networks have many parameters: one bias for each neuron, and one weight for every connection between neurons. These extra parameters enable the network to find more complicated boundaries.
For example, imagine that you’re trying to do the same map classification task, but the true border is far from a straight line.
We could try training a single-neuron classifier to approximate this border, but it would never work very well. In general, larger networks can do more complicated jobs, though they also need more training data.
From Maps to Cats
We’ve seen that we can make a neural network more capable by using more neurons. But so far, we’ve looked only at networks with two inputs. There’s no limit on how many inputs a neural network can have. Most useful tasks require networks with many inputs.
In our previous examples, the neuron’s two inputs were the longitude and latitude coordinates of points on a map. A neural network’s input numbers can also represent other kinds of data. For example, a number between 0 and 1 can stand for the gray scale value of a single pixel.
That means any pair of pixels can be plotted as a point in a two-dimensional space.
Likewise, pixel triplets correspond to points in a three-dimensional space.
More pixels require more dimensions. We can’t visualize anything higher than three, but researchers have developed ways to look at three-dimensional representations of these abstract spaces, akin to viewing a two-dimensional snapshot of a three-dimensional space. With nine dimensions, we can represent different patterns on a three-by-three grid.
To see how this can be useful, let’s take a big jump up from nine inputs to 2,500, representing a 50-by-50 grid of pixels. Different patterns on a grid of this size can depict meaningful images, like pictures of cats. Every cat picture corresponds to a different point in the 2,500-dimensional space.
Other points in this space correspond to pictures of coffee cups.
Given enough data points, we could train a large network to distinguish between cats and noncats.
All cat photos lie in some complicated region in the 2,500-dimensional space. A training algorithm would repeatedly tweak the network’s parameters until it finds the boundary around this impossible-to-visualize region.
A trained network would then be able to correctly classify new images that weren’t in the training data. Voilà: We’ve built a network that can “recognize” an image of a cat.
More Than Just Cats
Our cat detector network has many neurons and many inputs, but only one output. With more outputs, we could train the network to recognize many classes of objects, not just cats. Each class would correspond to a different region in the 2,500-dimensional space. More sophisticated image recognition networks have found applications in astrophysics, cell biology, medicine and many other fields.
Neural networks can also do tasks beyond classification. Large language models like ChatGPT are based on neural networks whose input and output numbers represent words. State-of-the-art networks are very large, with billions or trillions of parameters. That makes it very difficult to know exactly what different parts of the network are doing. Trying to understand what’s going on in large neural networks is a challenge that occupies many researchers today.