How to Create Art With Mathematics

The beautiful color illustration of frieze patterns above is taken from Frank A. Farris’ Creating Symmetry: The Artful Mathematics of Wallpaper Patterns (Princeton University Press, 2015), a math book that, unusually, makes an outstanding coffee-table book in addition to having deep mathematical content.
Lavished with many beautiful illustrations of this kind, Farris’ book is a joyful yet serious exploration of how mathematics can create beautiful patterns and provide us with a deep understanding of symmetry, one of the underlying principles of great art. “Euclid alone has looked on Beauty bare,” wrote the poet Edna St. Vincent Millay, and Frank Farris shows us what that means. His book uses the abstract, esoteric beauty of mathematical equations to create the universally appealing beauty of visual art. I believe our ability to find beauty in both mathematics and art reveals something deep about the human mind, a topic we may explore in the solution column. For now, let’s tackle today’s puzzles. They are inspired by the more elementary parts of Farris’ book, which discusses different types of symmetries in wallpaper, friezes and Escher-esque morphing patterns using a host of mathematical techniques involving groups, vector spaces, Fourier series, rosette functions, wave functions and several others. The puzzles below merely skim the surface of the connection between math and art that the book explores in depth, but they are designed to encourage all of our readers to create stunning visual patterns using mathematics. (Update: The solution is now available here.)
Question 1:
Look at the family of symmetrical curves below, one of which is featured in Farris’ book as a “mystery curve”:
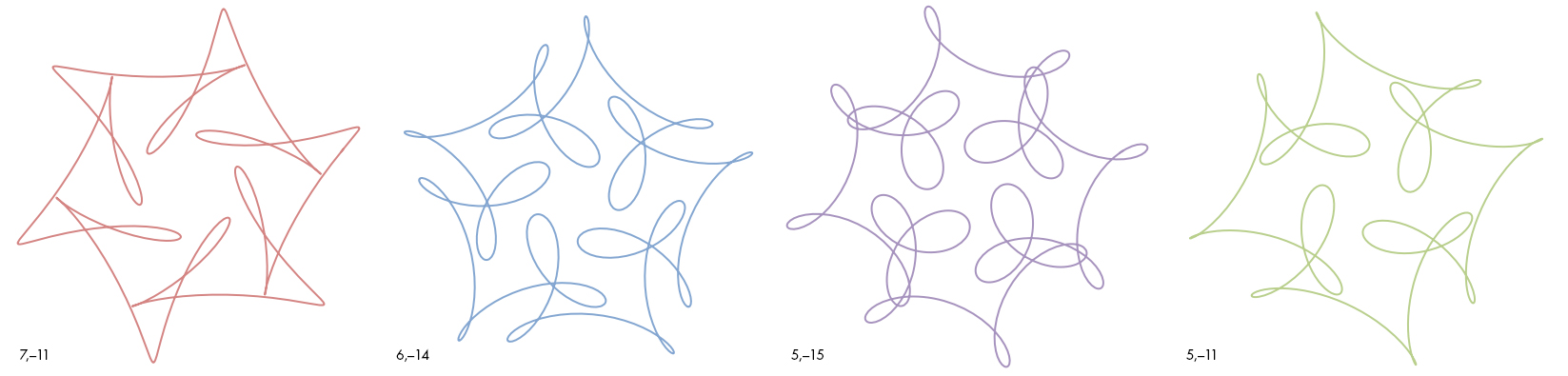
Each of these curves has an ordered pair of numbers associated with it, shown at the lower left of the curve. These two numbers determine the type of symmetry and complexity exhibited by the curve, and a simple mathematical relationship between the two numbers is required to generate the curve’s pleasant symmetry. In the second question below, we’ll give you the precise way these numbers are used to generate their curve. Without looking ahead, ponder these numbers and try to get an intuitive sense of how the curves change as the numbers do. Then look at curves A and B below and see if you can match them to the correct pairs of numbers, from the 10 choices given. Give your reasons for choosing your particular pairs and describe what you think the relationship is between the two numbers.
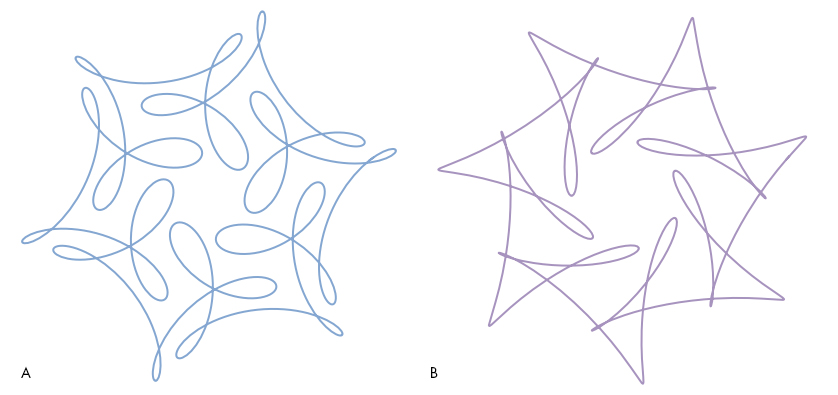
1. (5, –19) 2. (6, –19) 3. (7, –17) 4. (7, –12) 5. (7, –19)
6. (8, –20) 7. (8, –12) 8. (8, –13) 9. (8, –19) 10. (6, –24)
How are the numbers related to the curves, and how can we generate other similarly graceful curves? Our next two challenges arise from these questions. Question 2 requires some mathematical sophistication, but you can skip it if you wish and go straight to question 3, which only requires a willingness to explore and play, and create beauty.
Question 2:
The “mystery curve” from Farris’ book is the second one (6, –14) from question 1. The curve has a fivefold symmetry, which you can clearly make out in the image at right. Here’s the expression that generated this curve: (cos(t) + cos(6t)/2 + sin(14t)/3, sin(t) + sin(6t)/2 + cos(14t)/3).
Note that this is a parametric equation — the first half gives the x-coordinate and the second part the y-coordinate as the parameter t goes from 0 to 2π. The mystery is this: What do the coefficients 6 and 14 have to do with generating fivefold symmetry? Why did we use –14 instead of 14 in question 1? Can you explain how this formula works to a general audience?
Question 3:
Anyone can generate the above curve — use your favorite graphing app, or enter the above expression into Wolfram Alpha or the excellent graphic calculator Desmos. Now start playing with the parameters — change the coefficients, fiddle with the signs, do anything you want using sine and cosine terms. You can use the insights you gained from considering question 1 above — or not. Go wild! It’s like having a magic Spirograph whose pen never slips. Try to come up with the most pleasing curves you can. Submit the equations for your two or three most beautiful curves as comments to this column. We will publish a gallery of the curves our panel considers the most beautiful.
Happy puzzling. And may insight and creativity be with you!
Editor’s notes: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt.
If you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION” (it will not appear online, so solutions to the puzzle questions above should be submitted separately).
Note that we will hold comments for the first day to allow for independent contributions.
Update: The solution has been published here.



