Math Duo Maps the Infinite Terrain of Minimal Surfaces

Ted Kinsman/Science Source
Introduction
In the final months of 2011, Brian White would occasionally hear a tap on his Stanford University office door. Waiting outside would be two younger mathematicians, Fernando Codá Marques and André Neves, always with the same rough question: Did White have a few minutes to help them understand some confusing part of an obscure, several-hundred-page doctoral dissertation written three decades earlier?
The dissertation, by Jon Pitts, presented powerful machinery for constructing minimal surfaces — structures akin to soap films and bubbles — within a wide variety of shapes. Minimal surfaces, when they can be constructed, offer a lens through which to study the geometry of the surrounding space, and they turn up in a range of scientific settings, from the study of black holes to the design of biomolecules.
Yet over the years, Pitts’ dissertation had vanished from view, perhaps because it was incredibly hard reading. Marques and Neves were certain it was filled with untapped potential. “It was clear to us that the theory was completely underrated, completely unnoticed,” said Neves, now a professor at the University of Chicago.
Though White never asked why they were interested in Pitts’ work, the pair made each visit prepared to claim that it was “just academic interest,” Neves said. But they had a specific goal in mind — a proof of the Willmore conjecture, a 50-year-old question about finding, in some sense, the best possible doughnut shape (more about this later). After three months of wrestling with the ideas in Pitts’ dissertation, Marques and Neves succeeded in that goal, earning numerous awards and accolades.
But in the past few years, they have managed to push Pitts’ ideas much, much further. Pitts and his adviser, Frederick Almgren, had found a way to guarantee that every low-dimensional shape contains at least one minimal surface. Now, Marques and Neves, along with a cadre of young mathematicians that has sprung up around them, have built on Almgren and Pitts’ ideas to show that, in general, these shapes must in fact contain a multitude of minimal surfaces — infinitely many, crowding and jostling through every corner of the shape. “It is a big breakthrough,” wrote the distinguished geometer Karen Uhlenbeck, of the University of Texas, Austin, in an email.
“Just constructing a single [minimal surface] was a huge effort,” said Richard Schoen, of the University of California, Irvine, who was Neves’ doctoral adviser nearly 15 years ago. “That these exist in so much abundance is really an amazing fact.”
This renaissance in Almgren and Pitts’ theory has led to an explosion of activity in the past year or two. “Results have been coming so thick and fast, it’s a little hard to keep up,” White said. “To me, it’s very exciting and wonderful.”
Charting the Mountain Range
Dip a curved wire frame into a soap solution, or blow a soap bubble, and the liquid quickly forms the surface with the least possible area. The geometry of these “minimal” surfaces has occupied mathematicians for hundreds of years, and it arises in subjects from architecture, where it inspires the design of roofs and other structures, to the creation of microparticles for drug delivery. For instance, five years ago, when a team of scientists fabricated porous molecules that could hold drugs or hormones, they found that some of the molecules took on a structure like a gyroid, an infinitely repeating surface that looks, on every small patch, like a bit of soap film.
Technically, mathematicians only count the wire-frame soap films as minimal surfaces, not the soap bubbles, since in an abstract space with no air molecules, a soap bubble will collapse to a single point. But even a soap film on a wire isn’t perfectly satisfying to mathematicians. The interior forms a nice surface, but the wire frame acts as an abrupt punctuation mark. It’s natural to wonder, given such a surface, whether it could be extended beyond the wire boundary and still look like a soap film on every little patch. Sometimes this is possible, and the surface will extend out to infinity. Other times, the surface will come back around and awkwardly intersect itself or run into other difficulties.
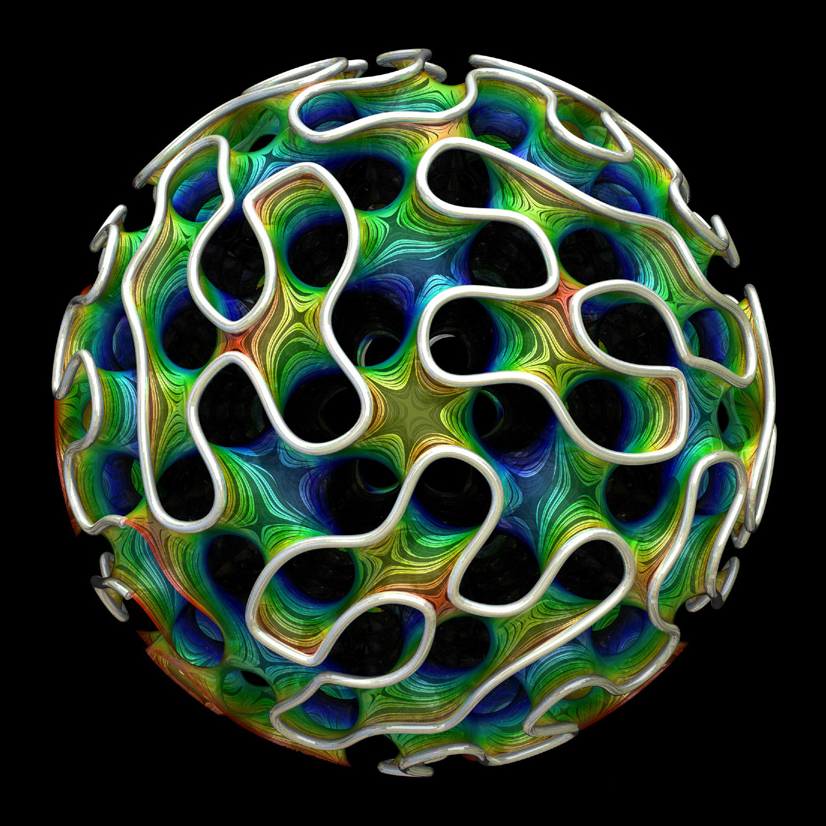
Gyroids are a type of minimal surface that have cropped up in the design of microparticles for drug delivery.
In ordinary space, these are the only possibilities. But mathematicians and scientists often have occasion to consider other types of worlds than the infinite three-dimensional space we’re used to thinking about — worlds that are curved or finite in size, such as the three-dimensional analogues of a sphere or doughnut surface. Within these shapes, a new, intriguing possibility emerges: minimal surfaces that curve back upon themselves and close up into a complete, finite shape that needs no wire support.
In relativity theory, these finite minimal surfaces appear as the event horizons of black holes. And when they can be found within some shape, they help mathematicians understand its geometry in a variety of ways: They provide a template for cutting the shape (or “manifold”) into potentially simpler pieces, and they point toward areas of positive curvature within the manifold — regions that curve inward, like a sphere or black hole, instead of spreading outward.
“We don’t know very much about manifolds of positive curvature,” Schoen said.
But proving that finite minimal surfaces exist inside a shape is often no easy matter. To see why, consider the two-dimensional version of this problem. The question of finding minimal surfaces makes sense in any dimension: Mathematicians simply consider a “surface” to be a shape whose dimension is one lower than the space it lives in. So in a two-dimensional world, the minimal surfaces are “geodesic” curves, built up from the shortest paths between nearby points.
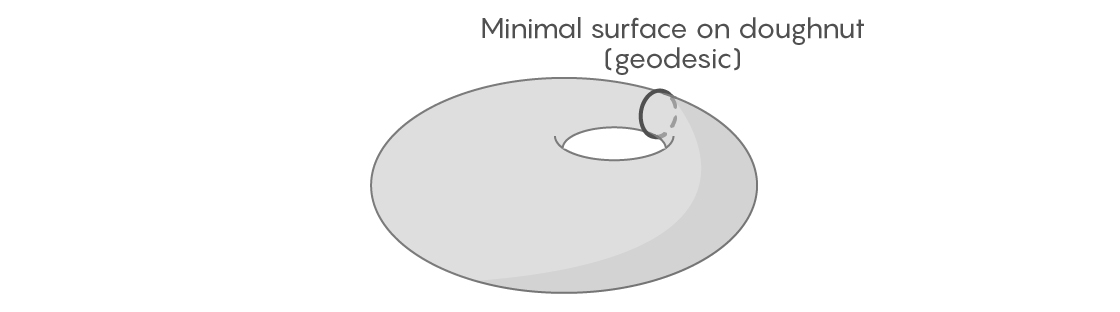
For some two-dimensional shapes, it is easy to find geodesics that close up into a finite loop. Take, for example, a doughnut surface — not even necessarily a nicely rounded, symmetric doughnut, but one with bumps and irregularities. If we wrapped a rubber band around the doughnut, passing through its central hole, we could imagine pulling it tight and then sliding it about the surface into all possible positions. One of these configurations must be the shortest, and that has to be a geodesic, since otherwise we could shorten it further.
But if our shape is a sphere instead of a doughnut, this approach fails. In a perfectly round sphere, it is easy to identify the geodesics: They are the equator and the other “great circles.” But on a bumpy sphere like Earth’s surface, it isn’t clear where the geodesics go, or whether any of them close up into a finite loop. You could imagine wrapping a rubber band around Earth, as we did with the doughnut. But if you slide it around trying to shorten it, it will shrink to a single point, since unlike the doughnut, the sphere has no hole on which the rubber band can get snagged.
However, this rubber band failure actually holds the seeds for success. In a round sphere, if we imagine a rubber band sitting on the equator, one way of shifting it about — introducing wiggles in it — will make it longer. Another way of moving it — sliding it straight up or down to a new latitude — will make it shorter. So the equator is the shortest curve from one point of view, and the longest curve from another.
That makes the equator analogous to the saddle point at the top of a mountain pass, which is the highest point in one direction (the route over the pass) and the lowest point in another direction (the route up to the surrounding peaks). This is not just a vague analogy: As a rule, minimal surfaces really are saddle points, but their mountain range lives in a world much harder to visualize than our ordinary one.
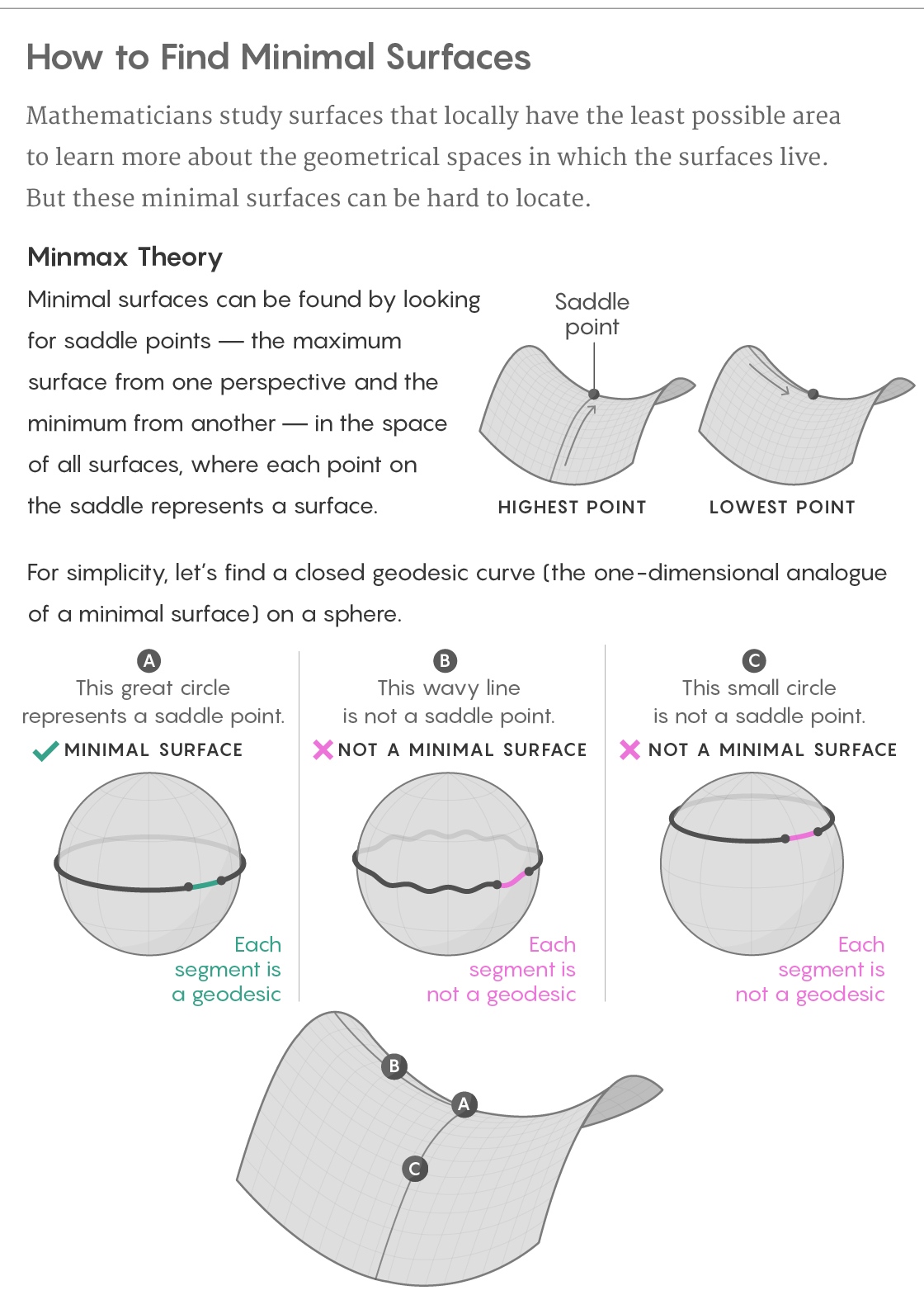
Lucy Reading-Ikkanda/Quanta Magazine
When we’re looking for the minimal surfaces within a shape, we can consider a new world that consists of all possible finite surfaces that live in the shape — let’s call this world “surface space.” Each point in surface space corresponds to an entire surface back in the original shape. Next, we can think of each surface’s area as determining the altitude of its corresponding point in surface space, so that our new world has a natural topography. Looking for minimal surfaces in our original shape translates into looking for saddle points in surface space.
In 1917, George Birkhoff used this approach to show that any sphere, bumpy or round, must have at least one closed geodesic. And about six decades later, in a tour-de-force extension of Birkhoff’s ideas, Almgren and Pitts mapped out the topography of surface space for all finite shapes of dimensions three through seven, and then used that topography to prove that such shapes always have at least one closed minimal surface. Pitts’ 1981 dissertation on this “minmax” theory — so named because a saddle point is both a minimum and a maximum — was “absolutely outstanding,” Neves said.
But it was also extraordinarily difficult. Few people understood the theory’s nuances, and some mathematicians studying it made claims that were never fully verified, Schoen said. “I don’t think there was ever any doubt that it was extremely interesting and important,” he said. But “it wasn’t clear how much of it was completely rigorous.”
Work on minmax theory gradually petered out. “[Pitts’] work was forgotten from the mathematical community for maybe 30 years,” Neves said. It was not resurrected until after Neves and Marques met each other in 2006 in the elevator of Fine Hall, Princeton University’s mathematics building.
Over the Mountain Pass
At the time, Marques was visiting Princeton to give a talk; Neves had recently begun a postdoctoral position there. Both native Portuguese speakers (Marques is from Brazil and Neves, from Portugal), they slipped easily into conversation. “It was the first time I’d talked to him, but he talked to me as if we were friends for 10 years,” recalled Marques, now a professor at Princeton.
And they found that discussing mathematics together came just as naturally. The two had different styles: Marques is patient, Neves more intense. But this, if anything, was a plus. “It’s very rare, I would say, that you find someone that complements you so much,” Marques said.
Both were eager to find some mathematical challenge they could really sink their teeth into. For several years, the pair threw ideas around whenever their paths crossed, to “see what sticks,” Neves said. “We’d have millions of ideas, and eventually one filters through and just becomes something formed.”
The big challenge that eventually filtered through was a famous problem called the Willmore conjecture. This asks for the doughnut shape that minimizes a quantity called Willmore energy, which, roughly speaking, measures how different the shape is from a round sphere. Willmore had conjectured in 1965 that the roundest doughnut is an especially symmetric shape called the Clifford torus, but no one had been able to prove this, despite many attempts.


After proving the Willmore conjecture in 2013, Fernando Codá Marques (top) and André Neves went on to achieve a breakthrough result in the study of minimal surfaces.
After proving the Willmore conjecture in 2013, Fernando Codá Marques (left) and André Neves went on to achieve a breakthrough result in the study of minimal surfaces.
Ana Menezes (Marques); Courtesy of André Neves
Marques and Neves developed a promising approach, but to make it work, they needed one final ingredient: minmax theory. They figured that mastering the theory and then writing up their paper would take two or three weeks — until they opened Pitts’ book. “We had a shock — like, what is this?” Neves said. “It’s an incredibly dry book.”
Single theorems went on for pages — and that was just to state the theorem, let alone prove it. It was difficult even to locate the main theorem. “I remember Fernando once came to my office and said, ‘I found the statement of the theorem!’” Neves said.
When they got stuck, they would put on their poker faces and ask for help from White, one of the only people who understood much of Pitts’ work (though White himself characterizes those discussions as “the blind leading the blind”; Pitts himself, who is a professor at Texas A&M University in College Station, stopped writing papers on minmax theory decades ago). “We were incredibly motivated, and so we were able to push through,” Neves recalled. “But it’s not for the faint of heart.”
By the time Marques and Neves had finished their proof of the Willmore conjecture, they understood minmax theory better than perhaps any other mathematicians. They were convinced that its potential extended much further than just the Willmore conjecture. “We knew we had this theory which was incredibly powerful,” Neves said. “Each time you use a method and you can prove a result that’s been open for a while, it tells you that there’s something to it. It tells you that it’s worthwhile to keep pushing and pushing.”
Almgren and Pitts’ minmax machinery generates not just a single saddle point, but an infinite list of them. In theory, these should correspond to an infinite list of minimal surfaces in the original shape. But Almgren and Pitts had not been able to show that the minimal surfaces produced in this way were all different surfaces. So the most they could conclude was that the original shape had at least one minimal surface.
After that, “the subject pretty much stopped,” Neves said. “This was the best result in more than 30 years.”
Some new ingredient was needed, and Marques and Neves found one. The infinite list of minmax surfaces, they showed in 2016, behaves — in a specific way — much like the frequencies of a drum.
The mathematician Hermann Weyl had shown in 1911 that the fundamental frequencies of a drum have a surprising property: Roughly speaking, the high frequencies depend only on the volume of the drum, not on its shape. Marques and Neves, together with Yevgeny Liokumovich of the Massachusetts Institute of Technology, showed that minmax surfaces satisfy a mathematical law similar to that of drum frequencies. In particular, the areas of the surfaces (especially the ones further out on the list) are roughly determined by the volume of the space they live in, but not its shape.
This result, which settled a decades-old conjecture, enabled Marques and Neves to show in 2017 — this time in collaboration with Kei Irie of the University of Tokyo — that for most shapes, the minmax list contains infinitely many different minimal surfaces. Even more, they showed, these surfaces are “dense”: they turn up near every point in the surrounding space. The intuition behind this deduction is that in order for the space’s volume to determine the areas of the minimal surfaces, these surfaces must somehow “see” the entire volume. This “suggests that these guys are everywhere in the manifold,” Marques said.
And a couple of months later, the pair, in collaboration with Marques’ graduate student Antoine Song, showed that as you go out along the list of minmax surfaces, these surfaces tend to fill space evenly — what mathematicians call “equidistribution.”
“When I heard the result about them being equidistributed, I was amazed,” White said. “It just seemed way beyond what people would be able to prove in my lifetime.”
In the past couple of years, other mathematicians have jumped into the action. In January, for instance, Xin Zhou of the University of California, Santa Barbara, built on Marques and Neves’ previous work to prove that for most shapes, every minimal surface on Almgren and Pitts’ list is different, bringing that question to a satisfying closure. “It does kind of make a nice package of this thing that’s been left open since the Almgren-Pitts thing in the ’80s,” White said.
This family of results covers almost every shape of dimension between three and seven — all but the most nicely rounded shapes, counterintuitively enough. But last June, Song managed to prove that every single shape in those dimensions, including the roundest shapes, has infinitely many closed minimal surfaces, settling yet another decades-old conjecture.
It remains to be seen whether denseness and equidistribution will also carry over into this broader setting, as well as which parts of minmax theory work in manifolds that aren’t compact and ones with dimension eight or higher (where a new paper already appears to have made some progress). Many of these questions are likely to be answered sooner rather than later, mathematicians predict.
“Things are going super fast,” Neves said. “Each week now I look at the [scientific preprint site] arxiv, and someone just solved something else.”
From one point of view, this body of work marks the end — or close to the end — of a story that has dangled unfinished for nearly four decades. But it is also a fresh beginning: Mathematicians are only starting to understand what these new insights about minimal surfaces could tell us about the spaces within which they live.
“I would guess that there should be other dramatic applications coming along, but I can’t say exactly what at this point,” Schoen said. “It’s going to be a major direction in geometry, I’m sure.”
Editor’s Note: André Neves was named a Simons Investigator in 2018. The Simons Foundation also funds this editorially independent magazine.



