Mathematicians Bridge Finite-Infinite Divide

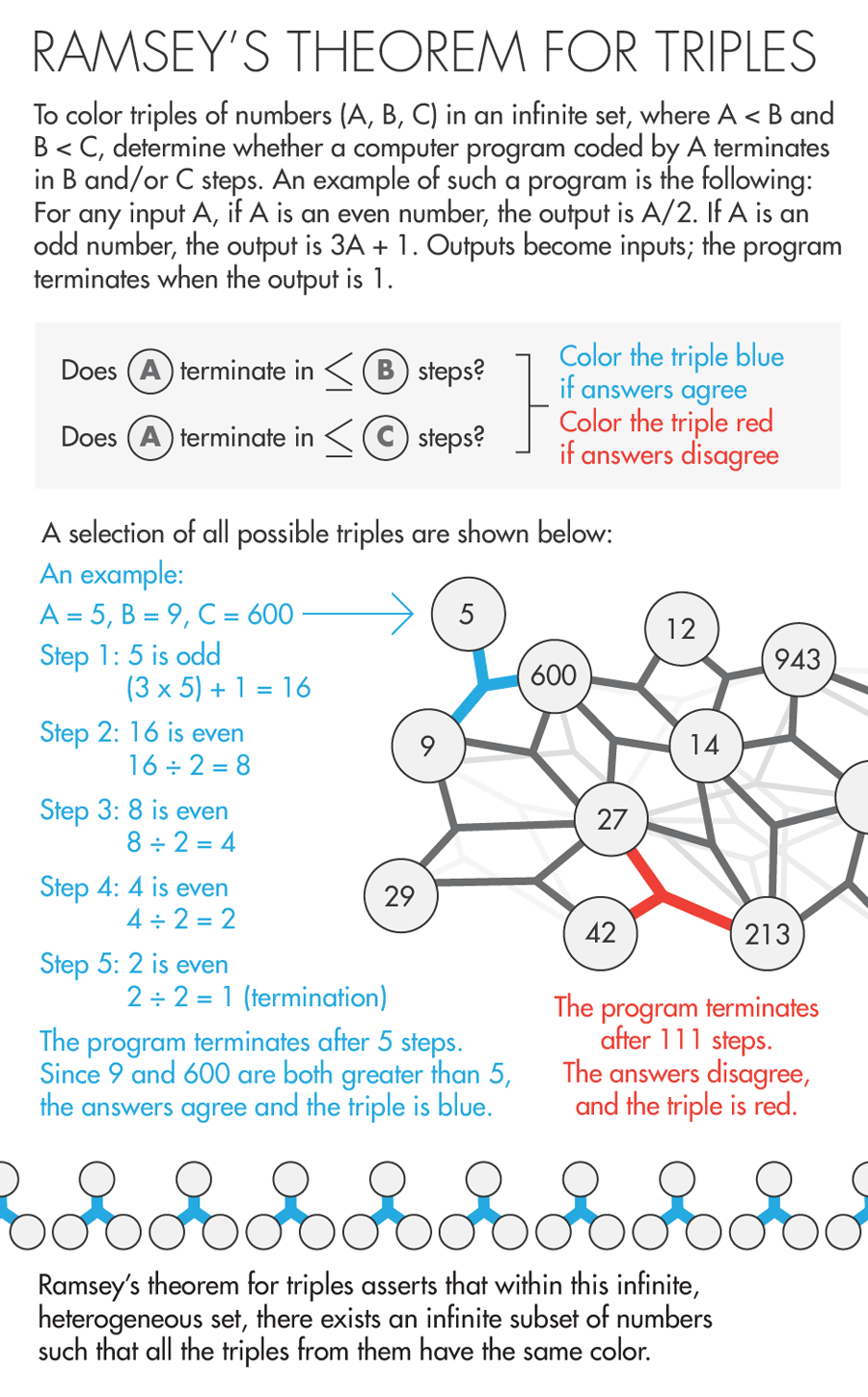
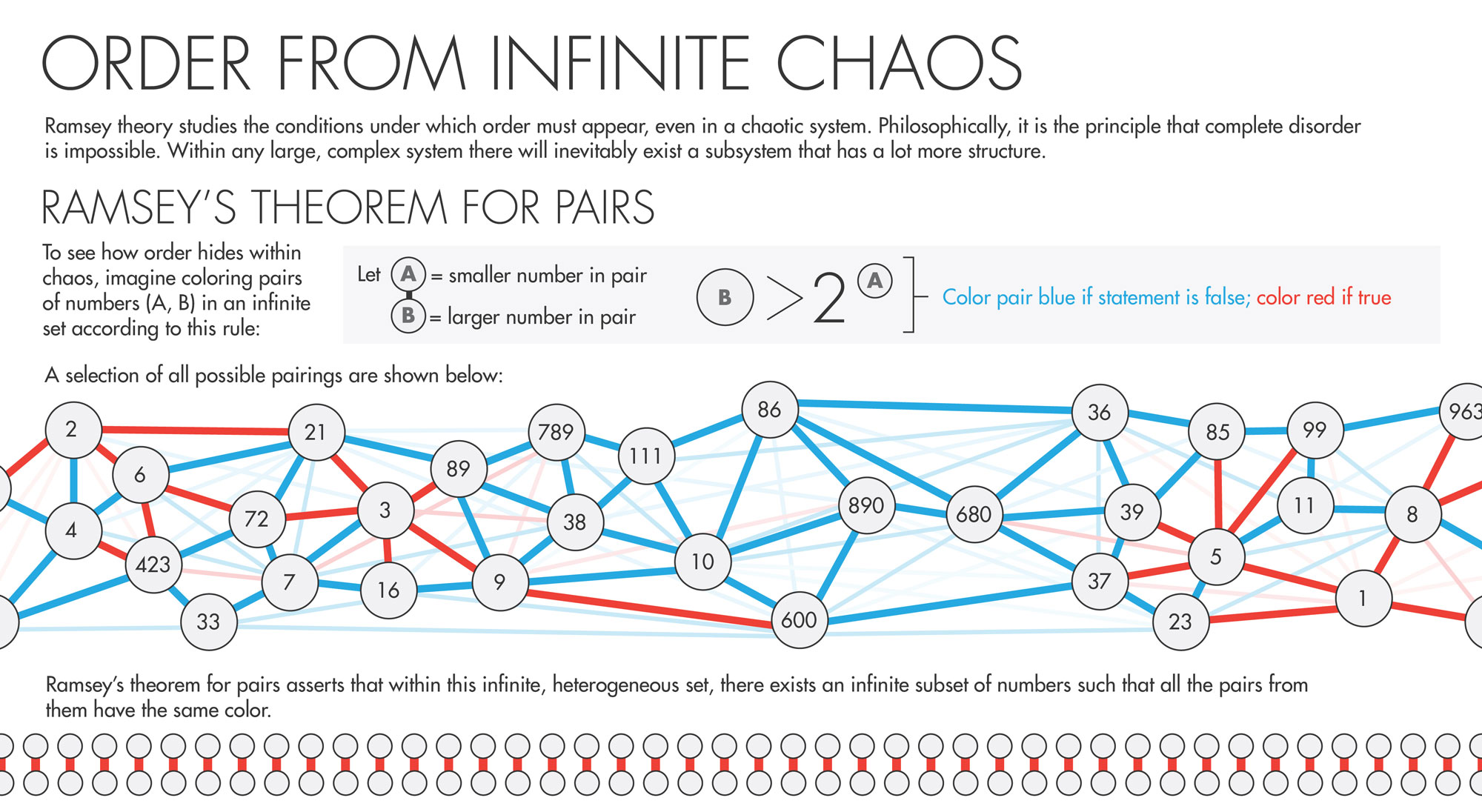
Ramsey’s theorem for pairs is thought to be the most complicated statement involving infinity that is known to be finitistically reducible. It invites you to imagine having in hand an infinite set of objects, such as the set of all natural numbers. Each object in the set is paired with all other objects. You then color each pair of objects either red or blue according to some rule. (The rule might be: For any pair of numbers A < B, color the pair blue if B < 2^A, and red otherwise.) When this is done, $latexRT_2^2$ states that there will exist an infinite monochromatic subset: a set consisting of infinitely many numbers, such that all the pairs they make with all other numbers are the same color. (Yokoyama, working with Slaman, is now generalizing the proof so that it holds for any number of colors.)

The colorable, divisible infinite sets in $latexRT_2^2$ are abstractions that have no analogue in the real world. And yet, Yokoyama and Patey’s proof shows that mathematicians are free to use this infinite apparatus to prove statements in finitistic mathematics — including the rules of numbers and arithmetic, which arguably underlie all the math that is required in science — without fear that the resulting theorems rest upon the logically shaky notion of infinity. That’s because all the finitistic consequences of $latexRT_2^2$ are “true” with or without infinity; they are guaranteed to be provable in some other, purely finitistic way. $latexRT_2^2$’s infinite structures “may make the proof easier to find,” explained Slaman, “but in the end you didn’t need them. You could give a kind of native proof — a [finitistic] proof.”

When Yokoyama set his sights on $latexRT_2^2$ as a postdoctoral researcher four years ago, he expected things to turn out differently. “To be honest, I thought actually it’s not finitistically reducible,” he said.

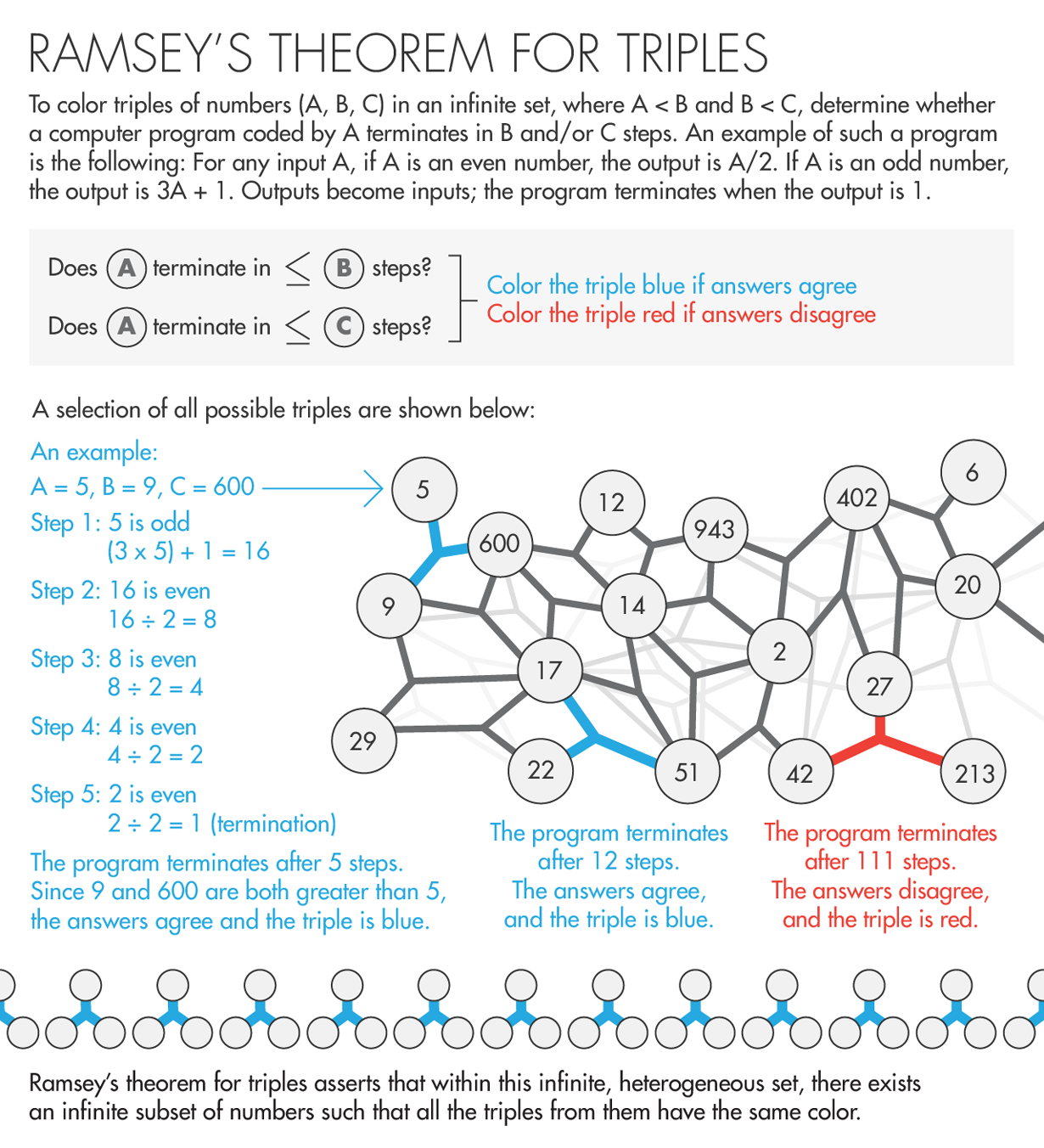
This was partly because earlier work proved that Ramsey’s theorem for triples, or $latexRT_2^3$, is not finitistically reducible: When you color trios of objects in an infinite set either red or blue (according to some rule), the infinite, monochrome subset of triples that $latexRT_2^3$ says you’ll end up with is too complex an infinity to reduce to finitistic reasoning. That is, compared to the infinity in $latexRT_2^2$, the one in $latexRT_2^3$ is, so to speak, more hopelessly infinite.

Even as mathematicians, logicians and philosophers continue to parse the subtle implications of Patey and Yokoyama’s result, it is a triumph for the “partial realization of Hilbert’s program,” an approach to infinity championed by the mathematician Stephen Simpson of Vanderbilt University. The program replaces an earlier, unachievable plan of action by the great mathematician David Hilbert, who in 1921 commanded mathematicians to weave infinity completely into the fold of finitistic mathematics. Hilbert saw finitistic reducibility as the only remedy for the skepticism then surrounding the new mathematics of the infinite. As Simpson described that era, “There were questions about whether mathematics was going into a twilight zone.”

The Rise of Infinity

The philosophy of infinity that Aristotle set out in the fourth century B.C. reigned virtually unchallenged until 150 years ago. Aristotle accepted “potential infinity” — the promise of the number line (for example) to continue forever — as a perfectly reasonable concept in mathematics. But he rejected as meaningless the notion of “actual infinity,” in the sense of a complete set consisting of infinitely many elements.

Aristotle’s distinction suited mathematicians’ needs until the 19th century. Before then, “mathematics was essentially computational,” said Jeremy Avigad, a philosopher and mathematician at Carnegie Mellon University. Euclid, for instance, deduced the rules for constructing triangles and bisectors — useful for bridge building — and, much later, astronomers used the tools of “analysis” to calculate the motions of the planets. Actual infinity — impossible to compute by its very nature — was of little use. But the 19th century saw a shift away from calculation toward conceptual understanding. Mathematicians started to invent (or discover) abstractions — above all, infinite sets, pioneered in the 1870s by the German mathematician Georg Cantor. “People were trying to look for ways to go further,” Avigad said. Cantor’s set theory proved to be a powerful new mathematical system. But such abstract methods were controversial. “People were saying, if you’re giving arguments that don’t tell me how to calculate, that’s not math.”

And, troublingly, the assumption that infinite sets exist led Cantor directly to some nonintuitive discoveries. He found that infinite sets come in an infinite cascade of sizes — a tower of infinities with no connection to physical reality. What’s more, set theory yielded proofs of theorems that were hard to swallow, such as the 1924 Banach-Tarski paradox, which says that if you break a sphere into pieces, each composed of an infinitely dense scattering of points, you can put the pieces together in a different way to create two spheres that are the same size as the original. Hilbert and his contemporaries worried: Was infinitistic mathematics consistent? Was it true?

Amid fears that set theory contained an actual contradiction — a proof of 0 = 1, which would invalidate the whole construct — math faced an existential crisis. The question, as Simpson frames it, was, “To what extent is mathematics actually talking about anything real? [Is it] talking about some abstract world that’s far from the real world around us? Or does mathematics ultimately have its roots in reality?”

Even though they questioned the value and consistency of infinitistic logic, Hilbert and his contemporaries did not wish to give up such abstractions — power tools of mathematical reasoning that in 1928 would enable the British philosopher and mathematician Frank Ramsey to chop up and color infinite sets at will. “No one shall expel us from the paradise which Cantor has created for us,” Hilbert said in a 1925 lecture. He hoped to stay in Cantor’s paradise and obtain proof that it stood on stable logical ground. Hilbert tasked mathematicians with proving that set theory and all of infinitistic mathematics is finitistically reducible, and therefore trustworthy. “We must know; we will know!” he said in a 1930 address in Königsberg — words later etched on his tomb.

However, the Austrian-American mathematician Kurt Gödel showed in 1931 that, in fact, we won’t. In a shocking result, Gödel proved that no system of logical axioms (or starting assumptions) can ever prove its own consistency; to prove that a system of logic is consistent, you always need another axiom outside of the system. This means there is no ultimate set of axioms — no theory of everything — in mathematics. When looking for a set of axioms that yield all true mathematical statements and never contradict themselves, you always need another axiom. Gödel’s theorem meant that Hilbert’s program was doomed: The axioms of finitistic mathematics cannot even prove their own consistency, let alone the consistency of set theory and the mathematics of the infinite.

This might have been less worrying if the uncertainty surrounding infinite sets could have been contained. But it soon began leaking into the realm of the finite. Mathematicians started to turn up infinitistic proofs of concrete statements about natural numbers — theorems that could conceivably find applications in physics or computer science. And this top-down reasoning continued. In 1994, Andrew Wiles used infinitistic logic to prove Fermat’s Last Theorem, the great number theory problem about which Pierre de Fermat in 1637 cryptically claimed, “I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.” Can Wiles’ 150-page, infinity-riddled proof be trusted?

With such questions in mind, logicians like Simpson have maintained hope that Hilbert’s program can be at least partially realized. Although not all of infinitistic mathematics can be reduced to finitistic reasoning, they argue that the most important parts can be firmed up. Simpson, an adherent of Aristotle’s philosophy who has championed this cause since the 1970s (along with Harvey Friedman of Ohio State University, who first proposed it), estimates that some 85 percent of known mathematical theorems can be reduced to finitistic systems of logic. “The significance of it,” he said, “is that our mathematics is thereby connected, via finitistic reducibility, to the real world.”

An Exceptional Case

Almost all of the thousands of theorems studied by Simpson and his followers over the past four decades have turned out (somewhat mysteriously) to be reducible to one of five systems of logic spanning both sides of the finite-infinite divide. For instance, Ramsey’s theorem for triples (and all ordered sets with more than three elements) was shown in 1972 to belong at the third level up in the hierarchy, which is infinitistic. “We understood the patterns very clearly,” said Henry Towsner, a mathematician at the University of Pennsylvania. “But people looked at Ramsey’s theorem for pairs, and it blew all that out of the water.”

A breakthrough came in 1995, when the British logician David Seetapun, working with Slaman at Berkeley, proved that $latexRT_2^2$ is logically weaker than $latexRT_2^3$ and thus below the third level in the hierarchy. The breaking point between $latexRT_2^2$ and $latexRT_2^3$ comes about because a more complicated coloring procedure is required to construct infinite monochromatic sets of triples than infinite monochromatic sets of pairs.

“Since then, many seminal papers regarding $latexRT_2^2$ have been published,” said Weiermann — most importantly, a 2012 result by Jiayi Liu (paired with a result by Carl Jockusch from the 1960s) showed that $latexRT_2^2$ cannot prove, nor be proved by, the logical system located at the second level in the hierarchy, one rung below $latexRT_2^3$. The level-two system is known to be finitistically reducible to “primitive recursive arithmetic,” a set of axioms widely considered the strongest finitistic system of logic. The question was whether $latexRT_2^2$ would also be reducible to primitive recursive arithmetic, despite not belonging at the second level in the hierarchy, or whether it required stronger, infinitistic axioms. “A final classification of $latexRT_2^2$ seemed out of reach,” Weiermann said.

But then in January, Patey and Yokoyama, young guns who have been shaking up the field with their combined expertise in computability theory and proof theory, respectively, announced their new result at a conference in Singapore. Using a raft of techniques, they showed that $latexRT_2^2$ is indeed equal in logical strength to primitive recursive arithmetic, and therefore finitistically reducible.

“Everybody was asking them, ‘What did you do, what did you do?’” said Towsner, who has also worked on the classification of $latexRT_2^2$ but said that “like everyone else, I did not get far.” “Yokoyama is a very humble guy. He said, ‘Well, we didn’t do anything new; all we did was, we used the method of indicators, and we used this other technique,’ and he proceeded to list off essentially every technique anyone has ever developed for working on this sort of problem.”

In one key step, the duo modeled the infinite monochromatic set of pairs in $latexRT_2^2$ using a finite set whose elements are “nonstandard” models of the natural numbers. This enabled Patey and Yokoyama to translate the question of the strength of $latexRT_2^2$ into the size of the finite set in their model. “We directly calculate the size of the finite set,” Yokoyama said, “and if it is large enough, then we can say it’s not finitistically reducible, and if it’s small enough, we can say it is finitistically reducible.” It was small enough.

$latexRT_2^2$ has numerous finitistic consequences, statements about natural numbers that are now known to be expressible in primitive recursive arithmetic, and which are thus certain to be logically consistent. Moreover, these statements — which can often be cast in the form “for every number X, there exists another number Y such that … ” — are now guaranteed to have primitive recursive algorithms associated with them for computing Y. “This is a more applied reading of the new result,” said Kohlenbach. In particular, he said, $latexRT_2^2$ could yield new bounds on algorithms for “term rewriting,” placing an upper limit on the number of times outputs of computations can be further simplified.

Some mathematicians hope that other infinitistic proofs can be recast in the $latexRT_2^2$ language and shown to be logically consistent. A far-fetched example is Wiles’ proof of Fermat’s Last Theorem, seen as a holy grail by researchers like Simpson. “If someone were to discover a proof of Fermat’s theorem which is finitistic except for involving some clever applications of $latexRT_2^2$,” he said, “then the result of Patey and Yokoyama would tell us how to find a purely finitistic proof of the same theorem.”

Simpson considers the colorable, divisible infinite sets in $latexRT_2^2$ “convenient fictions” that can reveal new truths about concrete mathematics. But, one might wonder, can a fiction ever be so convenient that it can be thought of as a fact? Does finitistic reducibility lend any “reality” to infinite objects — to actual infinity? There is no consensus among the experts. Avigad is of two minds. Ultimately, he says, there is no need to decide. “There’s this ongoing tension between the idealization and the concrete realizations, and we want both,” he said. “I’m happy to take mathematics at face value and say, look, infinite sets exist insofar as we know how to reason about them. And they play an important role in our mathematics. But at the same time, I think it’s useful to think about, well, how exactly do they play a role? And what is the connection?”

With discoveries like the finitistic reducibility of $latexRT_2^2$ — the longest bridge yet between the finite and the infinite — mathematicians and philosophers are gradually moving toward answers to these questions. But the journey has lasted thousands of years already, and seems unlikely to end anytime soon. If anything, with results like $latexRT_2^2$, Slaman said, “the picture has gotten quite complicated.”

This article was reprinted on Wired.com.