Mathematicians Disprove Conjecture Made to Save Black Holes

Maciej Rebisz for Quanta Magazine
Introduction
Nearly 40 years after it was proposed, mathematicians have settled one of the most profound questions in the study of general relativity. In a paper posted online last fall, mathematicians Mihalis Dafermos and Jonathan Luk have proven that the strong cosmic censorship conjecture, which concerns the strange inner workings of black holes, is false.
“I personally view this work as a tremendous achievement — a qualitative jump in our understanding of general relativity,” emailed Igor Rodnianski, a mathematician at Princeton University.
The strong cosmic censorship conjecture was proposed in 1979 by the influential physicist Roger Penrose. It was meant as a way out of a trap. For decades, Albert Einstein’s theory of general relativity had reigned as the best scientific description of large-scale phenomena in the universe. Yet mathematical advances in the 1960s showed that Einstein’s equations lapsed into troubling inconsistencies when applied to black holes. Penrose believed that if his strong cosmic censorship conjecture were true, this lack of predictability could be disregarded as a mathematical novelty rather than as a sincere statement about the physical world.
“Penrose came up with a conjecture that basically tried to wish this bad behavior away,” said Dafermos, a mathematician at Princeton University.
This new work dashes Penrose’s dream. At the same time, it fulfills his ambition by other means, showing that his intuition about the physics inside black holes was correct, just not for the reason he suspected.
Relativity’s Cardinal Sin
In classical physics, the universe is predictable: If you know the laws that govern a physical system and you know its initial state, you should be able to track its evolution indefinitely far into the future. The dictum holds true whether you’re using Newton’s laws to predict the future position of a billiard ball, Maxwell’s equations to describe an electromagnetic field, or Einstein’s theory of general relativity to predict the evolution of the shape of space-time. “This is the basic principle of all classical physics going back to Newtonian mechanics,” said Demetrios Christodoulou, a mathematician at ETH Zurich and a leading figure in the study of Einstein’s equations. “You can determine evolution from initial data.”
But in the 1960s mathematicians found a physical scenario in which Einstein’s field equations — which form the core of his theory of general relativity — cease to describe a predictable universe. Mathematicians and physicists noticed that something went wrong when they modeled the evolution of space-time inside a rotating black hole.
To understand what went wrong, imagine falling into the black hole yourself. First you cross the event horizon, the point of no return (though to you it looks just like ordinary space). Here Einstein’s equations still work as they should, providing a single, deterministic forecast for how space-time will evolve into the future.
Lucy Reading-Ikkanda/Quanta Magazine
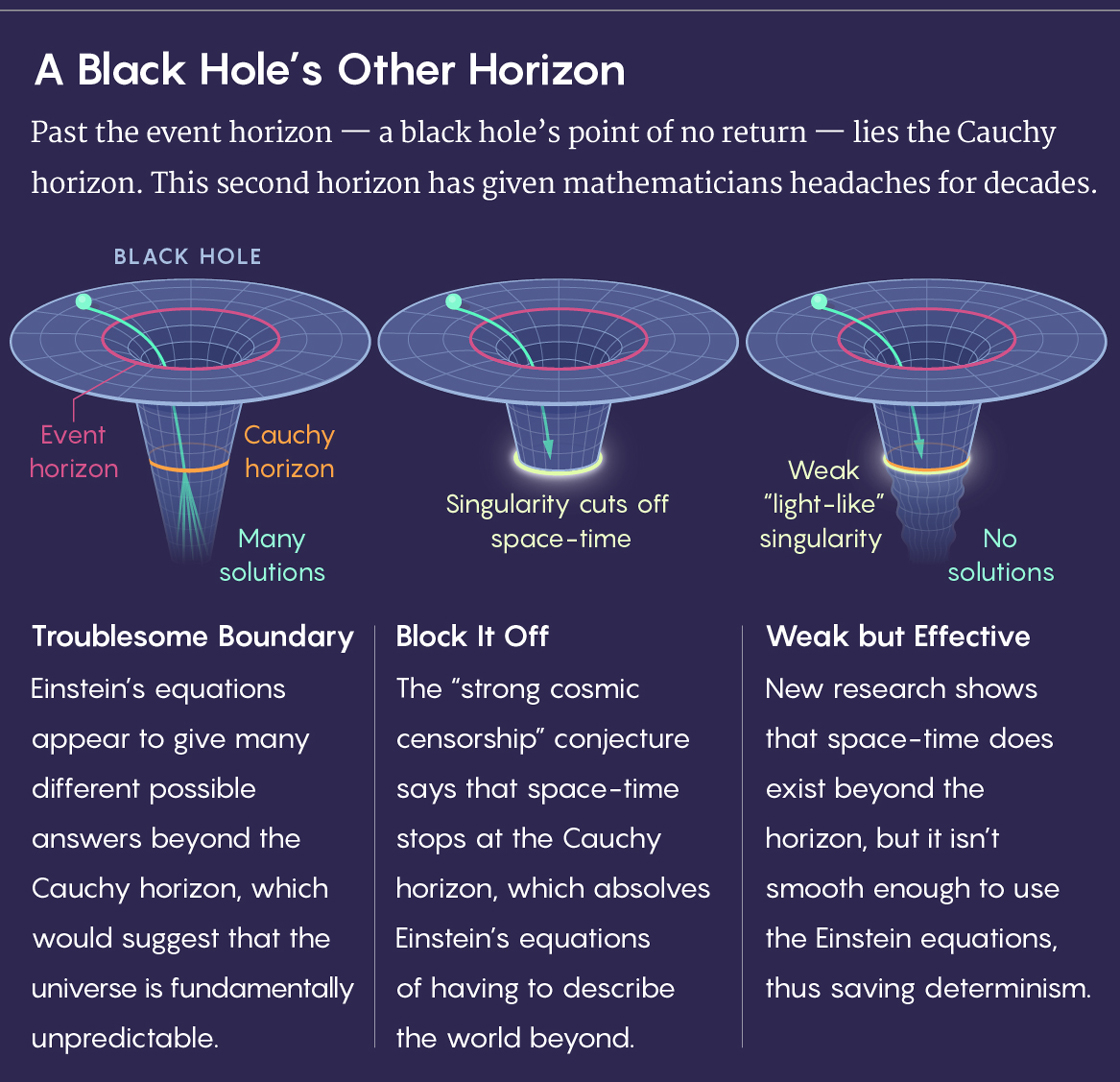
But as you continue to travel into the black hole, eventually you pass another horizon, known as the Cauchy horizon. Here things get screwy. Einstein’s equations start to report that many different configurations of space-time could unfold. They’re all different, yet they all satisfy the equations. The theory cannot tell us which option is true. For a physical theory, it’s a cardinal sin.
“The loss of predictability that we seem to find in general relativity was very disturbing,” said Eric Poisson, a physicist at the University of Guelph in Canada.
Roger Penrose proposed the strong cosmic censorship conjecture to restore predictability to Einstein’s equations. The conjecture says that the Cauchy horizon is a figment of mathematical thought. It might exist in an idealized scenario where the universe contains nothing but a single rotating black hole, but it can’t exist in any real sense.
The reason, Penrose argued, is that the Cauchy horizon is unstable. He said that any passing gravitational waves should collapse the Cauchy horizon into a singularity — a region of infinite density that rips space-time apart. Because the actual universe is rippled with these waves, a Cauchy horizon should never occur in the wild.
As a result, it’s nonsensical to ask what happens to space-time beyond the Cauchy horizon because space-time, as it’s regarded within the theory of general relativity, no longer exists. “This gives one a way out of this philosophical conundrum,” said Dafermos.
This new work shows, however, that the boundary of space-time established at the Cauchy horizon is less singular than Penrose had imagined.
To Save a Black Hole
Dafermos and Luk, a mathematician at Stanford University, proved that the situation at the Cauchy horizon is not quite so simple. Their work is subtle — a refutation of Penrose’s original statement of the strong cosmic censorship conjecture, but not a complete denial of its spirit.
Building on methods established a decade ago by Christodoulou, who was Dafermos’s adviser in graduate school, the pair showed that the Cauchy horizon can indeed form a singularity, but not the kind Penrose anticipated. The singularity in Dafermos and Luk’s work is milder than Penrose’s — they find a weak “light-like” singularity where he had expected a strong “space-like” singularity. This weaker form of singularity exerts a pull on the fabric of space-time but doesn’t sunder it. “Our theorem implies that observers crossing the Cauchy horizon are not torn apart by tidal forces. They may feel a pinch, but they are not torn apart,” said Dafermos in an email.
Because the singularity that forms at the Cauchy horizon is in fact milder than predicted by the strong cosmic censorship conjecture, the theory of general relativity is not immediately excused from considering what happens inside. “It still makes sense to define the Cauchy horizon because one can, if one wishes, continuously extend the space-time beyond it,” said Harvey Reall, a physicist at the University of Cambridge.
Dafermos and Luk prove that space-time extends beyond the Cauchy horizon. They also prove that from the same starting point, it can extend in any number of ways: Past the horizon “there are many such extensions that one could entertain, and there is no good reason to prefer one to the other,” said Dafermos.
Yet — and here’s the subtlety in their work — these nonunique extensions of space-time don’t mean that Einstein’s equations go haywire beyond the horizon.
Einstein’s equations work by quantifying how space-time changes over time. In mathematical language, it takes derivatives of an initial configuration of space-time. In order for it to be possible to take a derivative, space-time has to be sufficiently “smooth” — free of discontinuous jumps. Dafermos and Luk indicate that while space-time exists beyond the Cauchy horizon, this extended space-time isn’t smooth enough to actually satisfy Einstein’s equations. Thus, even with the strong cosmic censorship proven false, the equations are still spared the ignominy of outputting nonunique solutions.
“It makes sense to talk of the Cauchy horizon; however, you can’t continue beyond it as a solution of Einstein’s equations,” said Reall. “They’ve offered pretty convincing evidence that that is true, in my opinion.”
You could think of this outcome as a disappointing compromise: Even though you can extend space-time beyond the Cauchy horizon, Einstein’s equations can’t be solved. But it’s precisely the fact that this middle ground seems to exist that makes Dafermos and Luk’s work so interesting.
“This is people really discovering a new phenomenon in the Einstein equations,” said Rodnianski.
Correction: This article was updated on May 18, 2018, to reflect that it has been 40 years since Roger Penrose proposed the strong cosmic censorship conjecture, not 60 years.



