Mathematicians Find Wrinkle in Famed Fluid Equations
When two fluids move past each other at different speeds, complex instabilities arise. Mathematicians want to prove that the Navier-Stokes equations can predict what will happen in every possible case.
Introduction
The Navier-Stokes equations capture in a few succinct terms one of the most ubiquitous features of the physical world: the flow of fluids. The equations, which date to the 1820s, are today used to model everything from ocean currents to turbulence in the wake of an airplane to the flow of blood in the heart.
While physicists consider the equations to be as reliable as a hammer, mathematicians eye them warily. To a mathematician, it means little that the equations appear to work. They want proof that the equations are unfailing: that no matter the fluid, and no matter how far into the future you forecast its flow, the mathematics of the equations will still hold. Such a guarantee has proved elusive. The first person (or team) to prove that the Navier-Stokes equations will always work — or to provide an example where they don’t — stands to win one of seven Millennium Prize Problems endowed by the Clay Mathematics Institute, along with the associated $1 million reward.
Mathematicians have developed many ways of trying to solve the problem. New work posted online in September raises serious questions about whether one of the main approaches pursued over the years will succeed. The paper, by Tristan Buckmaster and Vlad Vicol of Princeton University, is the first result to find that under certain assumptions, the Navier-Stokes equations provide inconsistent descriptions of the physical world.
“We’re figuring out some of the inherent issues with these equations and why it’s quite possible [that] people have to rethink them,” said Buckmaster.
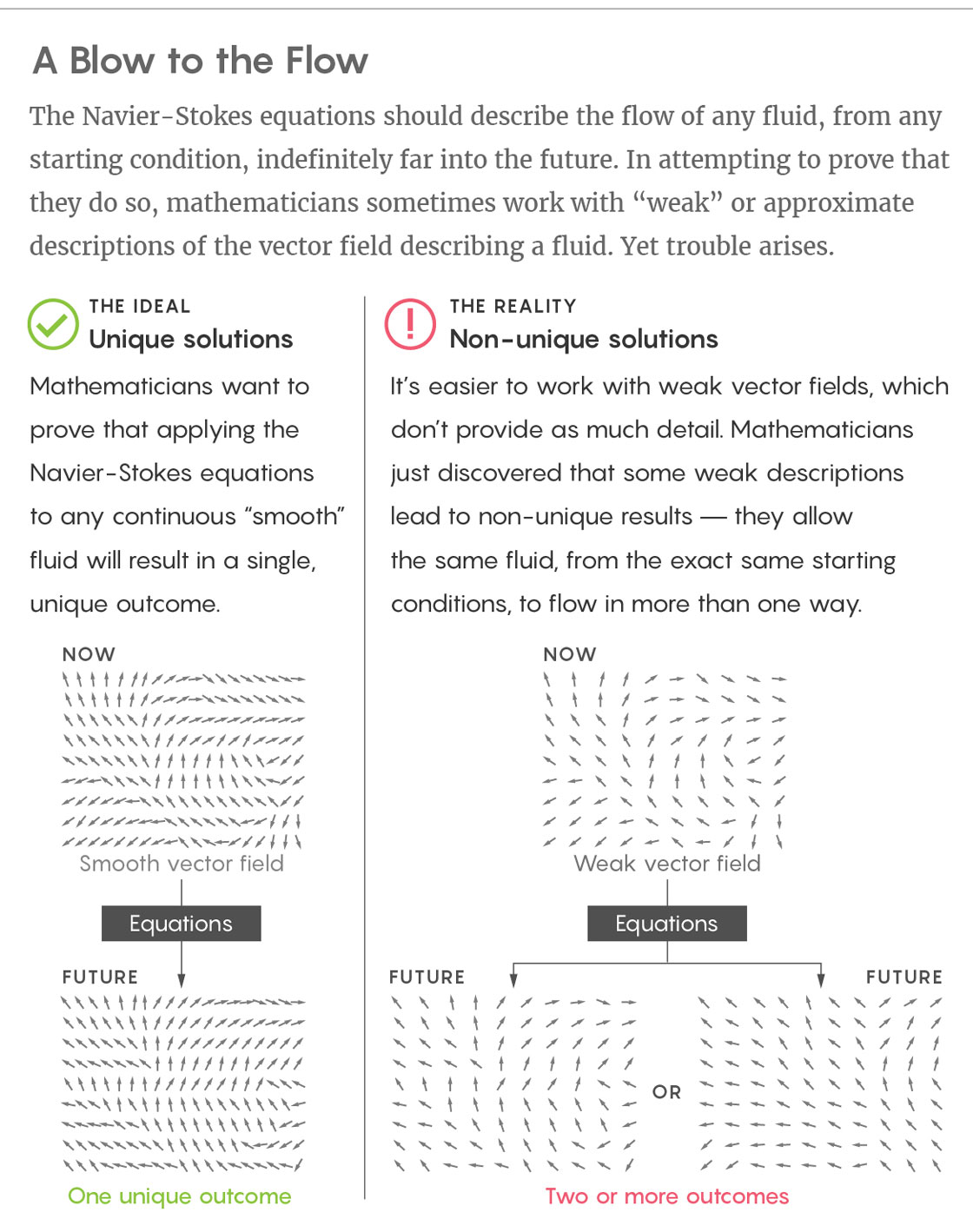
Buckmaster and Vicol’s work shows that when you allow solutions to the Navier-Stokes equations to be very rough (like a sketch rather than a photograph), the equations start to output nonsense: They say that the same fluid, from the same starting conditions, could end up in two (or more) very different states. It could flow one way or a completely different way. If that were the case, then the equations don’t reliably reflect the physical world they were designed to describe.
Blowing Up the Equations
To see how the equations can break down, first imagine the flow of an ocean current. Within it there may be a multitude of crosscurrents, with some parts moving in one direction at one speed and other areas moving in other directions at other speeds. These crosscurrents interact with one another in a continually evolving interplay of friction and water pressure that determines how the fluid flows.
Mathematicians model that interplay using a map that tells you the direction and magnitude of the current at every position in the fluid. This map, which is called a vector field, is a snapshot of the internal dynamics of a fluid. The Navier-Stokes equations take that snapshot and play it forward, telling you exactly what the vector field will look like at every subsequent moment in time.
A map of the wind functions much like a vector field: At every point, the wind has a particular direction and magnitude.
The equations work. They describe fluid flows as reliably as Newton’s equations predict the future positions of the planets; physicists employ them all the time, and they’ve consistently matched experimental results. Mathematicians, however, want more than anecdotal confirmation — they want proof that the equations are inviolate, that no matter what vector field you start with, and no matter how far into the future you play it, the equations always give you a unique new vector field.
This is the subject of the Millennium Prize problem, which asks whether the Navier-Stokes equations have solutions (where solutions are in essence a vector field) for all starting points for all moments in time. These solutions have to provide the exact direction and magnitude of the current at every point in the fluid. Solutions that provide information at such infinitely fine resolution are called “smooth” solutions. With a smooth solution, every point in the field has an associated vector that allows you to travel “smoothly” over the field without ever getting stuck at a point that has no vector — a point from which you don’t know where to move next.
Smooth solutions are a complete representation of the physical world, but mathematically speaking, they may not always exist. Mathematicians who work on equations like Navier-Stokes worry about this kind of scenario: You’re running the Navier-Stokes equations and observing how a vector field changes. After some finite amount of time, the equations tell you a particle in the fluid is moving infinitely fast. That would be a problem. The equations involve measuring changes in properties like pressure, friction, and velocity in the fluid — in the jargon, they take “derivatives” of these quantities — but you can’t take the derivative of an infinite value any more than you can divide by zero. So if the equations produce an infinite value, you can say they’ve broken down, or “blown up.” They can no longer describe subsequent states of your fluid.
Lucy Reading-Ikkanda/Quanta Magazine
Blowup is also a strong hint that your equations are missing something about the physical world they’re supposed to describe. “Maybe the equation is not capturing all the effects of the real fluid because in a real fluid we don’t expect” particles to ever start moving infinitely fast, said Buckmaster.
Solving the Millennium Prize problem involves either showing that blowup never happens for the Navier-Stokes equations or identifying the circumstances under which it does. One strategy mathematicians have pursued to do that is to first relax just how descriptive they require solutions to the equations to be.
From Weak to Smooth
When mathematicians study equations like Navier-Stokes, they sometimes start by broadening their definition of what counts as a solution. Smooth solutions require maximal information — in the case of Navier-Stokes, they require that you have a vector at every point in the vector field associated with the fluid. But what if you slackened your requirements and said that you only needed to be able to compute a vector for some points or only needed to be able to approximate vectors? These kinds of solutions are called “weak” solutions. They allow mathematicians to start feeling out the behavior of an equation without having to do all the work of finding smooth solutions (which may be impossible to do in practice).
“From a certain point of view, weak solutions are even easier to describe than actual solutions because you have to know much less,” said Camillo De Lellis, coauthor with László Székelyhidi of several important papers that laid the groundwork for Buckmaster and Vicol’s work.
Weak solutions come in gradations of weakness. If you think of a smooth solution as a mathematical image of a fluid down to infinitely fine resolution, weak solutions are like the 32-bit, or 16-bit, or 8-bit version of that picture (depending on how weak you allow them to be).
In 1934 the French mathematician Jean Leray defined an important class of weak solutions. Rather than working with exact vectors, “Leray solutions” take the average value of vectors in small neighborhoods of the vector field. Leray proved that it’s always possible to solve the Navier-Stokes equations when you allow your solutions to take this particular form. In other words, Leray solutions never blow up.
Leray’s achievement established a new approach to the Navier-Stokes problem: Start with Leray solutions, which you know always exist, and see if you can convert them into smooth solutions, which you want to prove always exist. It’s a process akin to starting with a crude picture and seeing if you can gradually dial up the resolution to get a perfect image of something real.
“One possible strategy is to show these weak Leray solutions are smooth, and if you show they’re smooth, you’ve solved the original Millennium Prize problem,” said Buckmaster.
There’s one more catch. Solutions to the Navier-Stokes equations correspond to real physical events, and physical events happen in just one way. Given that, you’d like your equations to have only one set of unique solutions. If the equations give you multiple possible solutions, they’ve failed.
Because of this, mathematicians will be able to use Leray solutions to solve the Millennium Prize problem only if Leray solutions are unique. Nonunique Leray solutions would mean that, according to the rules of Navier-Stokes, the exact same fluid from the exact same starting conditions could end up in two distinct physical states, which makes no physical sense and implies that the equations aren’t really describing what they’re supposed to describe.
Buckmaster and Vicol’s new result is the first to suggest that, for certain definitions of weak solutions, that might be the case.
Many Worlds
In their new paper, Buckmaster and Vicol consider solutions that are even weaker than Leray solutions — solutions that involve the same averaging principle as Leray solutions but also relax one additional requirement (known as the “energy inequality”). They use a method called “convex integration,” which has its origins in work in geometry by the mathematician John Nash and was imported more recently into the study of fluids by De Lellis and Székelyhidi.
Using this approach, Buckmaster and Vicol prove that these very weak solutions to the Navier-Stokes equations are nonunique. They demonstrate, for example, that if you start with a completely calm fluid, like a glass of water sitting still by your bedside, two scenarios are possible. The first scenario is the obvious one: The water starts still and remains still forever. The second is fantastical but mathematically permissible: The water starts still, erupts in the middle of the night, then returns to stillness.
“This proves nonuniqueness because from zero initial data you can construct at least two objects,” said Vicol.
Buckmaster and Vicol prove the existence of many nonunique weak solutions (not just the two described above) to the Navier-Stokes equations. The significance of this remains to be seen. At a certain point, weak solutions might become so weak that they stop really bearing on the smoother solutions they’re meant to imitate. If that’s the case, then Buckmaster and Vicol’s result might not lead far.
“Their result is certainly a warning, but you could argue it’s a warning for the weakest notion of weak solutions. There are many layers [of stronger solutions] on which you could still hope for much better behavior” in the Navier-Stokes equations, said De Lellis.
Buckmaster and Vicol are also thinking in terms of layers, and they have their sights set on Leray solutions — proving that those, too, allow for a multitrack physics in which the same fluid from the same position can take on more than one future form.
“Tristan and I think Leray solutions are not unique. We don’t have that yet, but our work is laying the foundation for how you’d attack the problem,” said Vicol.
This article was reprinted on Wired.com.
