Michael Atiyah’s Imaginative State of Mind
 Philipp Ammon for Quanta Magazine
Philipp Ammon for Quanta Magazine
Despite Michael Atiyah’s many accolades — he is a winner of both the Fields and the Abel prizes for mathematics; a past president of the Royal Society of London, the oldest scientific society in the world (and a past president of the Royal Society of Edinburgh); a former master of Trinity College, Cambridge; a knight and a member of the royal Order of Merit; and essentially Britain’s mathematical pope — he is nonetheless perhaps most aptly described as a matchmaker. He has an intuition for arranging just the right intellectual liaisons, oftentimes involving himself and his own ideas, and over the course of his half-century-plus career he has bridged the gap between apparently disparate ideas within the field of mathematics, and between mathematics and physics.
One day in the spring of 2013, for instance, as he sat in the Queen’s Gallery at Buckingham Palace awaiting the annual Order of Merit luncheon with Elizabeth II, Sir Michael made a match for his lifelong friend and colleague, Sir Roger Penrose, the great mathematical physicist.
Penrose had been trying to develop his “twistor” theory, a path toward quantum gravity that’s been in the works for nearly 50 years. “I had a way of doing it which meant going out to infinity,” Penrose said, “and trying to solve a problem out there, and then coming back again.” He thought there must be a simpler way. And right then and there Atiyah put his finger on it, suggesting Penrose make use of a type of “noncommutative algebra.”
“I thought, ‘Oh, my God,’” Penrose said. “Because I knew there was this noncommutative algebra which had been sitting there all this time in twistor theory. But I hadn’t thought of using it in this particular way. Some people might have just said, ‘That won’t work.’ But Michael could immediately see that there was a way in which you could make it work, and exactly the right thing to do.” Given the venue where Atiyah made the suggestion, Penrose dubbed his improved idea “palatial twistor theory.”
This is the power of Atiyah. Roughly speaking, he has spent the first half of his career connecting mathematics to mathematics, and the second half connecting mathematics to physics.
Atiyah is best known for the “index theorem,” devised in 1963 with Isadore Singer of the Massachusetts Institute of Technology (and properly called the Atiyah-Singer index theorem), connecting analysis and topology — a fundamental connection that proved to be important in both mathematical fields, and later in physics as well. Largely for this work, Atiyah won the Fields Medal in 1966 and the Abel Prize in 2004 (with Singer).
In the 1980s, methods gleaned from the index theorem unexpectedly played a role in the development of string theory — an attempt to reconcile the large-scale realm of general relativity and gravity with the small-scale realm of quantum mechanics — particularly with the work of Edward Witten, a string theorist at the Institute for Advanced Study in Princeton, N.J. Witten and Atiyah began an extended collaboration, and in 1990 Witten won the Fields Medal, the only physicist ever to win the prize, with Atiyah as his champion.
Now, at age 86, Atiyah is hardly lowering the bar. He’s still tackling the big questions, still trying to orchestrate a union between the quantum and the gravitational forces. On this front, the ideas are arriving fast and furious, but as Atiyah himself describes, they are as yet intuitive, imaginative, vague and clumsy commodities.
Still, he is relishing this state of free-flowing creativity, energized by his packed schedule. In hot pursuit of these current lines of investigation and contemplation, last December he delivered a double-header of lectures, back-to-back on the same day, at the University of Edinburgh, where he has been an honorary professor since 1997. He is keen to share his new ideas and, he hopes, attract supporters. To that end, in November he hosted a conference at the Royal Society of Edinburgh on “The Science of Beauty.” Quanta Magazine sat down with Atiyah at the Royal Society gathering and afterward, whenever he slowed down long enough to take questions. What follows is an edited version of those catch-as-catch-can conversations.
QUANTA MAGAZINE: Where do you trace the beginnings of your interest in beauty and science?
MICHAEL ATIYAH: I was born 86 years ago. That’s when my interest started. I was conceived in Florence. My parents were going to name me Michelangelo, but someone said, “That’s a big name for a small boy.” It would have been a disaster. I can’t draw. I have no talent at all.
You mentioned that something “clicked” during Roger Penrose’s lecture on “The Role of Art in Mathematics” and that you now have an idea for a collaborative paper. What is this clicking, the process or the state — can you describe it?
It’s the kind of thing that once you’ve seen it, the truth or veracity, it just stares you in the face. The truth is looking back at you. You don’t have to look for it. It’s shining on the page.
Is that generally how your ideas arrive?
This was a spectacular version. The crazy part of mathematics is when an idea appears in your head. Usually when you’re asleep, because that’s when you have the fewest inhibitions. The idea floats in from heaven knows where. It floats around in the sky; you look at it, and admire its colors. It’s just there. And then at some stage, when you try to freeze it, put it into a solid frame, or make it face reality, then it vanishes, it’s gone. But it’s been replaced by a structure, capturing certain aspects, but it’s a clumsy interpretation.
Have you always had mathematical dreams?
I think so. Dreams happen during the daytime, they happen at night. You can call them a vision or intuition. But basically they’re a state of mind — without words, pictures, formulas or statements. It’s “pre” all that. It’s pre-Plato. It’s a very primordial feeling. And again, if you try to grasp it, it always dies. So when you wake up in the morning, some vague residue lingers, the ghost of an idea. You try to remember what it was and you only get half of it right, and maybe that’s the best you can do.
Philipp Ammon for Quanta Magazine
Video: Michael Atiyah discusses beauty in mathematics.
Is imagination part of it?
Absolutely. Time travel in the imagination is cheap and easy — you don’t even need to buy a ticket. People go back and imagine they are part of the Big Bang, and then they ask the question of what came before.
What guides the imagination — beauty?
It’s not the kind of beauty that you can point to — it’s beauty in a much more abstract sense.
Not too long ago you published a study, with Semir Zeki, a neurobiologist at University College London, and other collaborators, on The Experience of Mathematical Beauty and Its Neural Correlates.
That’s the most-read article I’ve ever written! It’s been known for a long time that some part of the brain lights up when you listen to nice music, or read nice poetry, or look at nice pictures — and all of those reactions happen in the same place [the “emotional brain,” specifically the medial orbitofrontal cortex]. And the question was: Is the appreciation of mathematical beauty the same, or is it different? And the conclusion was, it is the same. The same bit of the brain that appreciates beauty in music, art and poetry is also involved in the appreciation of mathematical beauty. And that was a big discovery.
You reached this conclusion by showing mathematicians various equations while a functional MRI recorded their response. Which equation won out as most beautiful?
Ah, the most famous of all, Euler’s equation: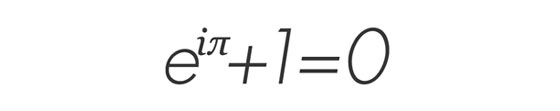 It involves π; the mathematical constant e [Euler’s number, 2.71828 …]; i, the imaginary unit; 1; and 0 — it combines all the most important things in mathematics in one formula, and that formula is really quite deep. So everybody agreed that that was the most beautiful equation. I used to say it was the mathematical equivalent of Hamlet’s phrase “To be, or not to be” — very short, very succinct, but at the same time very deep. Euler’s equation uses only five symbols, but it also encapsulates beautifully deep ideas, and brevity is an important part of beauty.
It involves π; the mathematical constant e [Euler’s number, 2.71828 …]; i, the imaginary unit; 1; and 0 — it combines all the most important things in mathematics in one formula, and that formula is really quite deep. So everybody agreed that that was the most beautiful equation. I used to say it was the mathematical equivalent of Hamlet’s phrase “To be, or not to be” — very short, very succinct, but at the same time very deep. Euler’s equation uses only five symbols, but it also encapsulates beautifully deep ideas, and brevity is an important part of beauty.
You are especially well-known for two supremely beautiful works, not only the index theorem but also K-theory, developed with the German topologist Friedrich Hirzebruch. Tell me about K-theory.
The index theorem and K-theory are actually two sides of the same coin. They started out different, but after a while they became so fused together that you can’t disentangle them. They are both related to physics, but in different ways.
K-theory is the study of flat space, and of flat space moving around. For example, let’s take a sphere, the Earth, and let’s take a big book and put it on the Earth and move it around. That’s a flat piece of geometry moving around on a curved piece of geometry. K-theory studies all aspects of that situation — the topology and the geometry. It has its roots in our navigation of the Earth.
The maps we used to explore the Earth can also be used to explore both the large-scale universe, going out into space with rockets, and the small-scale universe, studying atoms and molecules. What I’m doing now is trying to unify all that, and K-theory is the natural way to do it. We’ve been doing this kind of mapping for hundreds of years, and we’ll probably be doing it for thousands more.
Did it surprise you that K-theory and the index theorem turned out to be important in physics?
Oh, yes. I did all this geometry not having any notion that it would be linked to physics. It was a big surprise when people said, “Well, what you’re doing is linked to physics.” And so I learned physics quickly, talking to good physicists to find out what was happening.
How did your collaboration with Witten come about?
I met him in Boston in 1977, when I was getting interested in the connection between physics and mathematics. I attended a meeting, and there was this young chap with the older guys. We started talking, and after a few minutes I realized that the younger guy was much smarter than the old guys. He understood all the mathematics I was talking about, so I started paying attention to him. That was Witten. And I’ve kept in touch with him ever since.
What was he like to work with?
In 2001, he invited me to Caltech, where he was a visiting professor. I felt like a graduate student again. Every morning I would walk into the department, I’d go to see Witten, and we’d talk for an hour or so. He’d give me my homework. I’d go away and spend the next 23 hours trying to catch up. Meanwhile, he’d go off and do half a dozen other things. We had a very intense collaboration. It was an incredible experience because it was like working with a brilliant supervisor. I mean, he knew all the answers before I got them. If we ever argued, he was right and I was wrong. It was embarrassing!
You’ve said before that the unexpected interconnections that pop up occasionally between math and physics are what appeal to you most — you like finding yourself wading into unfamiliar territory.
Right; well, you see, a lot of mathematics is predictable. Somebody shows you how to solve one problem, and you do the same thing again. Every time you take a step forward you’re following in the steps of the person who came before. Every now and again, somebody comes along with a totally new idea and shakes everybody up. To start with, people don’t believe it, and then when they do believe it, it leads in a totally new direction. Mathematics comes in fits and starts. It has continuous development, and then it has discontinuous jumps, when suddenly somebody has a new idea. Those are the ideas that really matter. When you get them, they have major consequences. We’re about due another one. Einstein had a good idea 100 years ago, and we need another one to take us forward.
But the approach has to be more investigative than directive. If you try to direct science, you only get people going in the direction you told them to go. All of science comes from people noticing interesting side paths. You’ve got to have a very flexible approach to exploration and allow different people to try different things. Which is difficult, because unless you jump on the bandwagon, you don’t get a job.
Worrying about your future, you have to stay in line. That’s the worst thing about modern science. Fortunately, when you get to my age, you don’t need to bother about that. I can say what I like.
These days, you’re trying out some new ideas in hopes of breaking the stalemate in physics?
Well, you see, there’s atomic physics — electrons and protons and neutrons, all the stuff of which atoms are made. At these very, very, very small scales, the laws of physics are much the same, but there is also a force you ignore, which is the gravitational force. Gravity is present everywhere because it comes from the entire mass of the universe. It doesn’t cancel itself out, it doesn’t have positive or negative value, it all adds up. So however far away the black holes and galaxies are, they all exert a very small force everywhere in the universe, even in an electron or proton. But physicists say, “Ah, yes, but it’s so small you can ignore it; we don’t measure things that small, we do perfectly well without it.” My starting point is that that is a mistake. If you correct that mistake, you get a theory that is much better.
I’m now looking again at some of the ideas that were around 100 years ago and that were discarded at the time because people couldn’t understand what the ideas were trying to get at. How does matter interact with gravity? Einstein’s theory was that if you put a bit of matter in, it changes the curvature of space. And when the curvature of space changes, it acts on the matter. It’s a very complicated feedback mechanism.
I’m going back to Einstein and [Paul] Dirac and looking at them again with new eyes, and I think I’m seeing things that people missed. I’m filling in the holes of history, taking account of new discoveries. Archaeologists dig things up, or historians find a new manuscript, and that sheds an entirely new light. So that’s what I’ve been doing. Not by going into libraries, but by sitting in my room at home, thinking. If you think long enough, you get a good idea.
So you’re saying that the gravitational force can’t be ignored?
I think all the difficulty physicists have had comes from ignoring that. You shouldn’t ignore it. And the point is, I believe the mathematics gets simplified if you feed it in. If you leave it out, you make things more difficult for yourself.
Most people would say you don’t need to worry about gravitation when you look at atomic physics. The scale is so small that, for the kind of calculations we do, it can be ignored. In some sense, if you just want answers, that’s correct. But if you want understanding, then you’ve made a mistake in that choice.
If I’m wrong, well, I made a mistake. But I don’t think so. Because once you pick this idea up, there are all sorts of nice consequences. The mathematics fits together. The physics fits together. The philosophy fits together.
What does Witten think of your new ideas?
Well, it’s a challenge. Because when I talked to him in the past about some of my ideas, he dismissed them as hopeless, and he gave me 10 different reasons why they’re hopeless. Now I think I can defend my ground. I’ve spent a lot of time thinking, coming at it from different angles, and coming back to it. And I’m hoping I can persuade him that there is merit to my new approach.
You’re risking your reputation, but you think it’s worth it.
My reputation is established as a mathematician. If I make a mess of it now, people will say, “All right, he was a good mathematician, but at the end of his life he lost his marbles.”
A friend of mine, John Polkinghorne, left physics just as I was going in; he went into the church and became a theologian. We had a discussion on my 80th birthday and he said to me, “You’ve got nothing to lose; you just go ahead and think what you think.” And that’s what I’ve been doing. I’ve got all the medals I need. What could I lose? So that’s why I’m prepared to take a gamble that a young researcher wouldn’t be prepared to take.
Are you surprised to be so charged up about new ideas at this stage of your career?
One of my sons said to me, “Impossible, Dad. Mathematicians do all their best work by the time they’re 40. And you’re over 80. It’s impossible for you to have a good idea now.”
If you’re still awake and alert mentally when you’re over 80, you’ve got the advantage that you’ve lived a long time and you’ve seen many things, and you get perspective. I’m 86 now, and it’s in the last few years that I’ve had these ideas. New ideas come along and you pick up bits here and there, and the time is ripe now, whereas it might not have been ripe five or 10 years ago.
Is there one big question that has always guided you?
I always want to try to understand why things work. I’m not interested in getting a formula without knowing what it means. I always try to dig behind the scenes, so if I have a formula, I understand why it’s there. And understanding is a very difficult notion.
People think mathematics begins when you write down a theorem followed by a proof. That’s not the beginning, that’s the end. For me the creative place in mathematics comes before you start to put things down on paper, before you try to write a formula. You picture various things, you turn them over in your mind. You’re trying to create, just as a musician is trying to create music, or a poet. There are no rules laid down. You have to do it your own way. But at the end, just as a composer has to put it down on paper, you have to write things down. But the most important stage is understanding. A proof by itself doesn’t give you understanding. You can have a long proof and no idea at the end of why it works. But to understand why it works, you have to have a kind of gut reaction to the thing. You’ve got to feel it.
This article was reprinted on ScientificAmerican.com and Wired.com.