How to Cut Cake Fairly and Finally Eat It Too

Olena Shmahalo/Quanta Magazine
Introduction
Two young computer scientists have figured out how to fairly divide cake among any number of people, setting to rest a problem mathematicians have struggled with for decades. Their work has startled many researchers who believed that such a fair-division protocol was probably impossible.
Cake-cutting is a metaphor for a wide range of real-world problems that involve dividing some continuous object, whether it’s cake or, say, a tract of land, among people who value its features differently — one person yearning for chocolate frosting, for example, while another has his eye on the buttercream flowers. People have known at least since biblical times that there’s a way to divide such an object between two people so that neither person envies the other: one person cuts the cake into two slices that she values equally, and the other person gets to choose her favorite slice. In the book of Genesis, Abraham (then known as Abram) and Lot used this “I cut, you choose” procedure to divide land, with Abraham deciding where to divide and Lot choosing between Jordan and Canaan.
Around 1960, mathematicians devised an algorithm that can produce a similarly “envy-free” cake division for three players. But until now, the best they had come up with for more than three players was a procedure created in 1995 by political scientist Steven Brams of New York University and mathematician Alan Taylor of Union College in Schenectady, New York, which is guaranteed to produce an envy-free division, but it is “unbounded,” meaning that it might need to run for a million steps, or a billion, or any large number, depending on the players’ cake preferences.
Brams and Taylor’s algorithm was hailed as a breakthrough at the time, but “the fact that it wasn’t bounded I think was a huge shortcoming,” said Ariel Procaccia, a computer scientist at Carnegie Mellon University and one of the creators of Spliddit, a free online tool that provides fair-division algorithms for tasks like dividing chores or rent among roommates.

All Is Not Fair in Cake-Cutting and Math
Over the past 50 years, many mathematicians and computer scientists, including Procaccia, had convinced themselves that there was probably no bounded, envy-free algorithm for dividing cake among n players.
“This is the very problem that got me into the subject of fair division,” said Walter Stromquist, a mathematics professor at Bryn Mawr College in Pennsylvania who proved some of the seminal results on cake cutting in 1980. “I have thought all my life that I would come back to it when I had time and prove that this particular extension of the result was impossible.”
But in April, two computer scientists defied expectations by posting a paper online describing an envy-free cake-cutting algorithm whose running time depends only on the number of players, not on their individual preferences. One of the pair — 27-year-old Simon Mackenzie, a postdoctoral researcher at Carnegie Mellon — will present the pair’s findings on Oct. 10 at the 57th annual IEEE Symposium on Foundations of Computer Science, one of computer science’s pre-eminent conferences.

The algorithm is extraordinarily complex: Dividing a cake among n players can require as many as n^n^n^n^n^n steps and a roughly equivalent number of cuts. Even for just a handful of players, this number is greater than the number of atoms in the universe. But the researchers already have ideas for making the algorithm much simpler and faster, said the other half of the team, Haris Aziz, a 35-year-old computer scientist at the University of New South Wales and Data61, a data research group in Australia.
For the people who study the theory of fair division, this is “definitely the biggest result in decades,” Procaccia said.
Pieces of Cake
Aziz and Mackenzie’s new algorithm builds on an elegant procedure that mathematicians John Selfridge and John Conway independently came up with around 1960 for dividing a cake among three people.
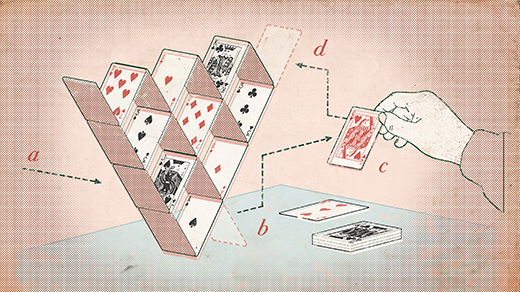
If Alice, Bob and Charlie want to share a cake, the algorithm starts by having Charlie cut the cake into three slices that are equally valuable from his perspective. Alice and Bob are each asked to point to their favorite slices, and if they like different slices, we’re done — they each take their favorite, Charlie takes the remaining slice, and everyone goes home happy.
If Alice and Bob have the same favorite, then Bob is asked to trim a little cake off that slice so that what remains is equal in value to his second-favorite slice; the trimmed bit is set aside for later. Now Alice gets to choose her favorite piece from among the three slices, and then Bob gets to choose, with the requirement that if Alice didn’t choose the trimmed slice, he must take it. Charlie gets the third slice.
At this stage, none of the players envy each other. Alice is happy since she got to choose first; Bob is happy since he got one of his two equally preferred top choices; and Charlie is happy because he got one of his three original pieces, all of which are equal in his eyes.
But there’s still the trimmed bit to be divided. What makes it possible to divide this bit without creating still more trimmings, and getting into an infinite cycle of trimming and choosing, is the fact that Charlie is more than merely satisfied with the cake he has gotten so far; he would not feel cheated even if the player with the trimmed slice gets all the cake that’s waiting to be allocated, since the trimmed slice plus the trimming equals one of the original slices. Aziz and Mackenzie describe this relationship by saying that Charlie “dominates” the player who got the trimmed slice.
Now if, for example, Alice was the one who got the trimmed slice, the algorithm proceeds as follows: Bob cuts the trimmings into three pieces that he values equally, and then first Alice gets to choose a piece, then Charlie, then Bob. Everyone is happy: Alice because she got to choose first, Charlie because he gets a slice he likes better than Bob’s (and he didn’t care how much Alice took), and Bob because the three slices are equal in his view.
Brams and Taylor used the notion of domination (without calling it that) in designing their 1995 algorithm, but they couldn’t push the idea far enough to get a bounded algorithm. For the next 20 years, neither could anyone else. “I don’t think it’s for lack of trying,” Procaccia said.
Rookie Cake-Cutters
When Aziz and Mackenzie decided to tackle the problem a couple of years ago, they were comparative newcomers to the cake-cutting problem. “We did not have as much background as people who have been intensely working on it would have,” Aziz said. “Although that is mostly a disadvantage, in this case it was somewhat of an advantage, because we were not thinking in the same way.”
Aziz and Mackenzie wet their feet by studying the three-player problem from scratch, and their analysis eventually led them to find a bounded envy-free algorithm for the four-player case, which they posted online last year.
They couldn’t immediately see how to extend their algorithm to more than four players, but they dived feverishly into the problem. “After we submitted our paper for the four-agent case, we were really keen that we should try it before someone much more experienced, much more clever would generalize it to the n-agent case,” Aziz said. After about a year, their efforts succeeded.
As with the Selfridge-Conway algorithm, Aziz and Mackenzie’s complicated protocol repeatedly asks individual players to cut cake into n equal pieces, then asks other players to make trims and choose pieces of cake. But the algorithm also carries out other steps, such as periodically exchanging portions of players’ cake stashes in a carefully controlled way, with an eye toward increasing the number of domination relationships between players.
These domination relationships allow Aziz and Mackenzie to reduce the complexity of the problem: If, for example, three players dominate all the others, those three can be sent away with their slices of cake — they’ll be happy no matter who gets the remaining trimmings. Now there are fewer players to worry about, and after a bounded number of such steps, everyone has been satisfied and all the cake given out.
“Seeing, in retrospect, how complicated the algorithm is, it’s not surprising that it took a long time before somebody found one,” Procaccia said. But Aziz and Mackenzie already think that they can simplify their algorithm considerably, to one that doesn’t need the cake exchanges and takes fewer than n^n^n steps. They are currently writing up these new results, Aziz said.
Even a simpler such algorithm would be unlikely to have practical implications, Brams cautioned, since the cake portions that players receive would typically include many tiny crumbs from different parts of the cake — not a feasible approach if you’re dividing something like a tract of land.
But for mathematicians and computer scientists who study cake cutting, the new result “resets the subject,” Stromquist said.
Now that researchers know it’s possible to fairly divide cake in a bounded number of steps, the next goal, Procaccia said, is to understand the huge gulf between Aziz and Mackenzie’s upper bound and the existing lower bound on the number of cuts needed to divide a cake. Procaccia had previously proved that an envy-free cake-cutting algorithm will require at least about n2 steps — but that bound is minuscule compared to n^n^n^n^n^n or even n^n^n.
Researchers now have to figure out how to close this gap, Aziz said. “I think there can be progress in both directions.”
This article was reprinted on ScientificAmerican.com and in Spanish at Investigacionyciencia.es.