New Geometric Perspective Cracks Old Problem About Rectangles

Does a closed loop include the corners of every kind of rectangle?
Vignette for Quanta Magazine
Introduction
In mid-March, the mathematicians Joshua Greene and Andrew Lobb found themselves in the same situation: locked down and struggling to adjust while the COVID-19 pandemic grew outside their doors. They decided to cope by throwing themselves into their research.
“I think the pandemic was really kind of galvanizing,” said Greene, a professor at Boston College. “We each decided it would be best to lean into some collaborations to sustain us.”
One of the problems the two friends looked at was a version of a century-old unsolved question in geometry.
“The problem is so easy to state and so easy to understand, but it’s really hard,” said Elizabeth Denne of Washington and Lee University.
It starts with a closed loop — any kind of curvy path that ends where it starts. The problem Greene and Lobb worked on predicts, basically, that every such path contains sets of four points that form the vertices of rectangles of any desired proportion.
While this “rectangular peg problem” seems like the kind of question a high school geometry student might settle with a ruler and compass, it has resisted mathematicians’ best efforts for decades. And when Greene and Lobb set out to tackle it, they didn’t have any particular reason to expect they’d fare better.
Of all the different projects he was working on, Greene said, “I thought this was probably the least promising one.”
But as the pandemic surged, Greene and Lobb, who is at Durham University in England and the Okinawa Institute of Science and Technology, held weekly Zoom calls and had a quick succession of insights. Then, on May 19, as parts of the world were just beginning to reopen, they emerged in their own way and posted a solution.
Their final proof — showing the predicted rectangles do indeed exist — transports the problem into an entirely new geometric setting. There, the stubborn question yields easily.
“It’s sort of weird,” said Richard Schwartz of Brown University. “It was just the right idea for this problem.”
Rethinking Rectangles
The rectangular peg problem is a close offshoot of a question posed by the German mathematician Otto Toeplitz in 1911. He predicted that any closed curve contains four points that can be connected to form a square. His “square peg problem” remains unsolved.
“It’s an old thorny problem that nobody has been able to crack,” Greene said.
To understand why the problem is so hard, it’s important to know something about the kinds of curves the square peg problem talks about, which matters for Greene and Lobb’s proof, too.
The pair solved a problem about closed curves that are both “continuous” and “smooth.” Continuous means they have no breaks. Smooth means they’re continuous and also have no corners. Smooth, continuous curves are the ones you’d likely draw if you sat down with pencil and paper. They’re “easier to get our hands on,” said Greene.
Smooth, continuous curves contrast with curves that are merely continuous, but not smooth — the type of curve that features in Toeplitz’s square peg conjecture. This type of curve can have corners — places where they veer suddenly in different directions. One prominent example of a curve with many corners is the fractal Koch snowflake, which in fact is made of nothing but corners. The Koch snowflake, and other curves like it, cannot be analyzed using calculus and related methods, a fact that makes them especially hard to study.
“Some continuous [non-smooth] curves are really nasty,” Denne said.
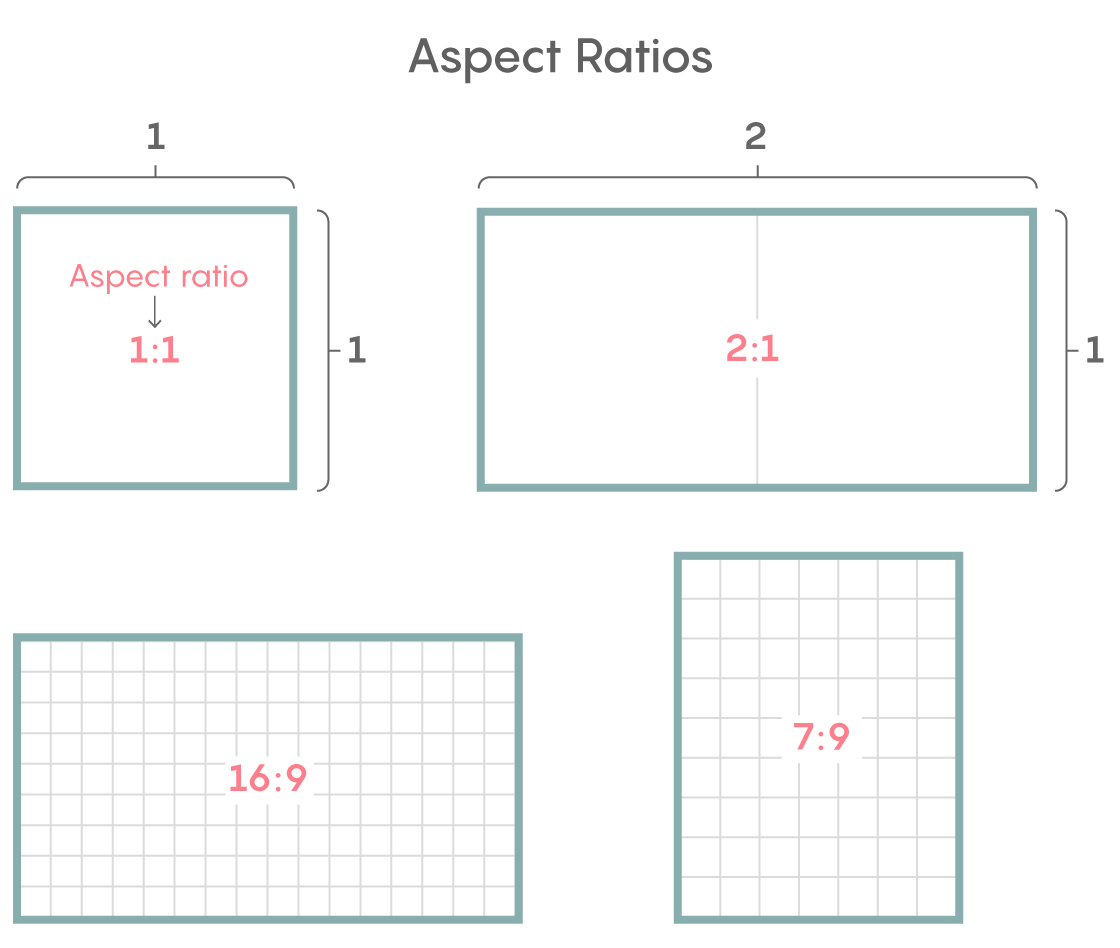
But again, the problem Greene and Lobb solved involves curves that are smooth, and therefore continuous. And instead of determining whether such curves always have four points that make a square — a question that was solved for smooth, continuous curves in 1929 — they investigated whether such curves always have sets of four points that form rectangles of all “aspect ratios,” meaning the ratios of their side lengths. For a square the aspect ratio is 1:1, while for many high-definition televisions it’s 16:9.
Samuel Velasco/Quanta Magazine
The first major progress on the rectangular peg problem was made in a proof from the late-1970s by Herbert Vaughan. The proof initiated a new way of thinking about the geometry of a rectangle and established methods that many mathematicians, including Greene and Lobb, later picked up.
“Everybody knows this proof,” Greene said. “It’s kind of folklore and the sort of thing you learn over a lunch table discussion around the common room.”
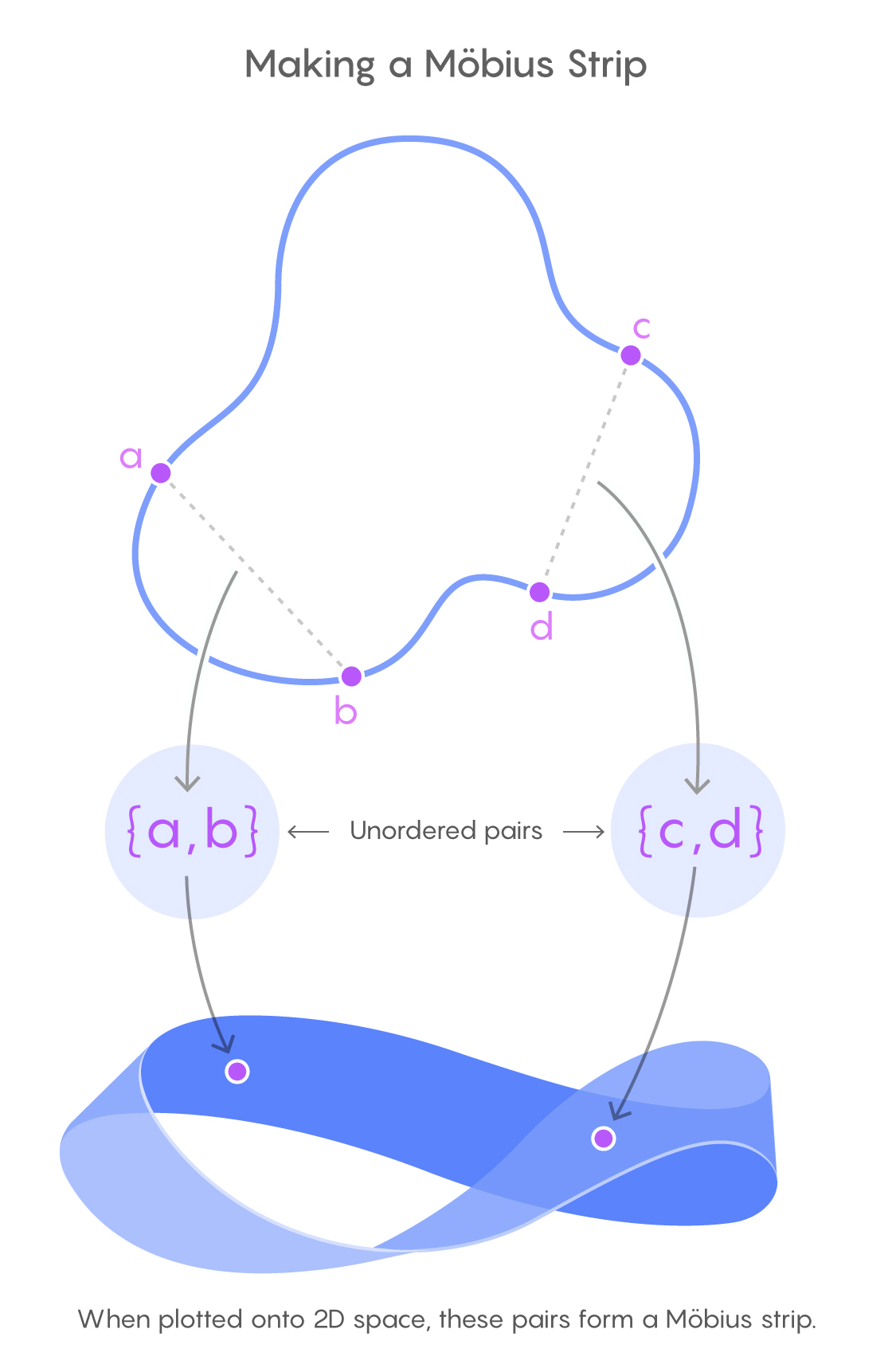
Instead of thinking of a rectangle as four connected points, Vaughan thought of it as two pairs of points that have a particular relationship with each other.
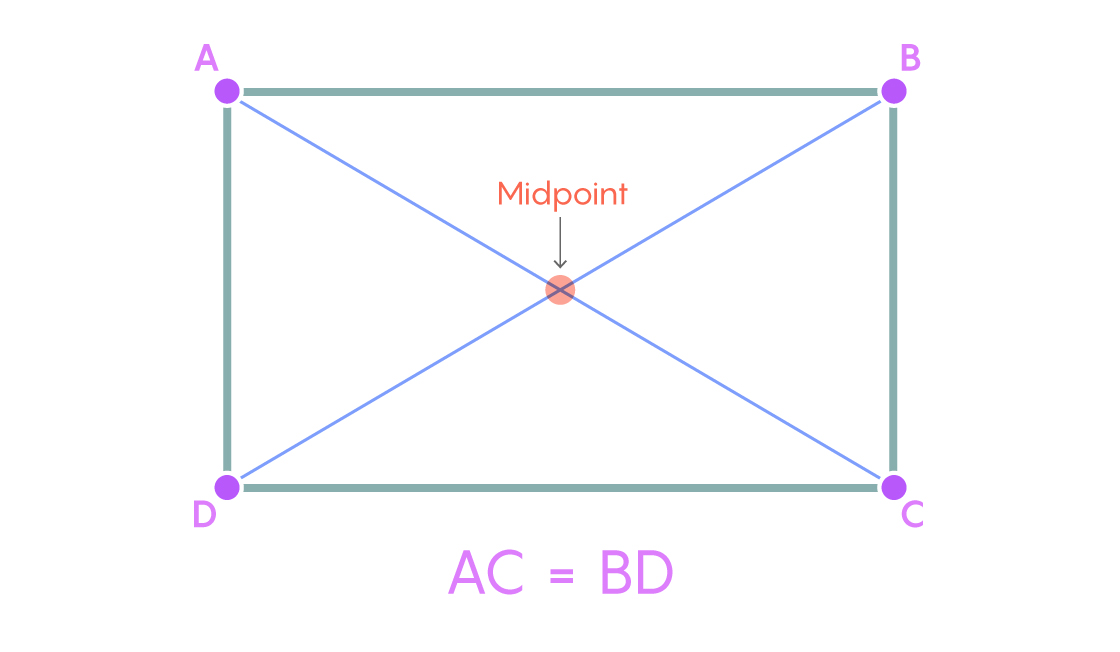
Samuel Velasco/Quanta Magazine
Picture a rectangle whose vertices are labeled ABCD, clockwise from the top left. In this rectangle, the distance between the pair of points AC (along the diagonal of the rectangle) is the same as the distance between the pair of points BD (along the other diagonal). The two line segments also intersect at their midpoints.
So if you’re looking for rectangles on a closed loop, one way to pursue them is to look for pairs of points on it that share this property: They form equal-length line segments with the same midpoint. And to find them, it’s important to come up with a systematic way of thinking about them.
To get a sense of what that means, let’s start with something simpler. Take the standard number line. Pick two points on it — say the numbers 7 and 8 — and plot them as a single point in the xy-plane (7, 8). Pairs of the same point are allowed too (7, 7). Now consider all possible pairs of numbers that can be extracted from the number line (it’s a lot!). If you were to plot all those pairs of points, you’d fill in the entire two-dimensional xy-plane. Another way of stating this is to say that the xy-plane “parameterizes,” or collects in an orderly way, all pairs of points on the number line.
Vaughan did something similar for pairs of points on a closed curve. (Like the number line, it’s one-dimensional, only it also curves in on itself.) He realized that if you take pairs of points from the curve and plot them — without worrying about which point is the x coordinate and which one is the y — you don’t get the flat xy-plane. Instead, you get a surprising shape: a Möbius strip, which is a two-dimensional surface that has only one side.
Samuel Velasco/Quanta Magazine
In a way this makes sense. To see why, pick a pair of points on the curve and label them x and y. Now travel from x to y along one arc of the curve while traveling from y to x along the complementary arc of the curve. As you do so, you move through all pairs of points on the curve, beginning and ending with the unordered pair (x, y). But as you do so, you return to where you started, only with your orientation flipped. This orientation-flipping loop of unordered points forms the core of a Möbius strip.
This Möbius strip provides mathematicians with a new object to analyze in order to solve the rectangular peg problem. And Vaughan used that fact to prove that every such curve contains at least four points that form a rectangle.
Four-Dimensional Answers
Greene and Lobb’s proof built on Vaughan’s work. But it also combined several additional results, some of which were only available very recently. The final proof is like a precision instrument, which has just the right combination of ideas to produce the outcome they wanted.
One of the first big ingredients of their proof appeared in November 2019 when a Princeton graduate student named Cole Hugelmeyer posted a paper that introduced a new way of analyzing Vaughan’s Möbius strip. This work involved a mathematical process called an embedding, in which you take an object and transplant it into a geometric space. Greene and Lobb would eventually take Hugelmeyer’s technique and move it into yet another geometric space. But to see what they did you first need to know what he did.
Here’s a simple example of what an embedding is.
Start with a one-dimensional line. Each point on the line is defined by a single number. Now “embed” that line in two-dimensional space — which is to say, just graph it in the plane.
Once you embed the line in the xy-plane, each point on it becomes defined by two numbers — the x and y coordinates that specify exactly where in the plane that point lies. Given this setup, you can then start to analyze the line using the techniques of two-dimensional geometry.
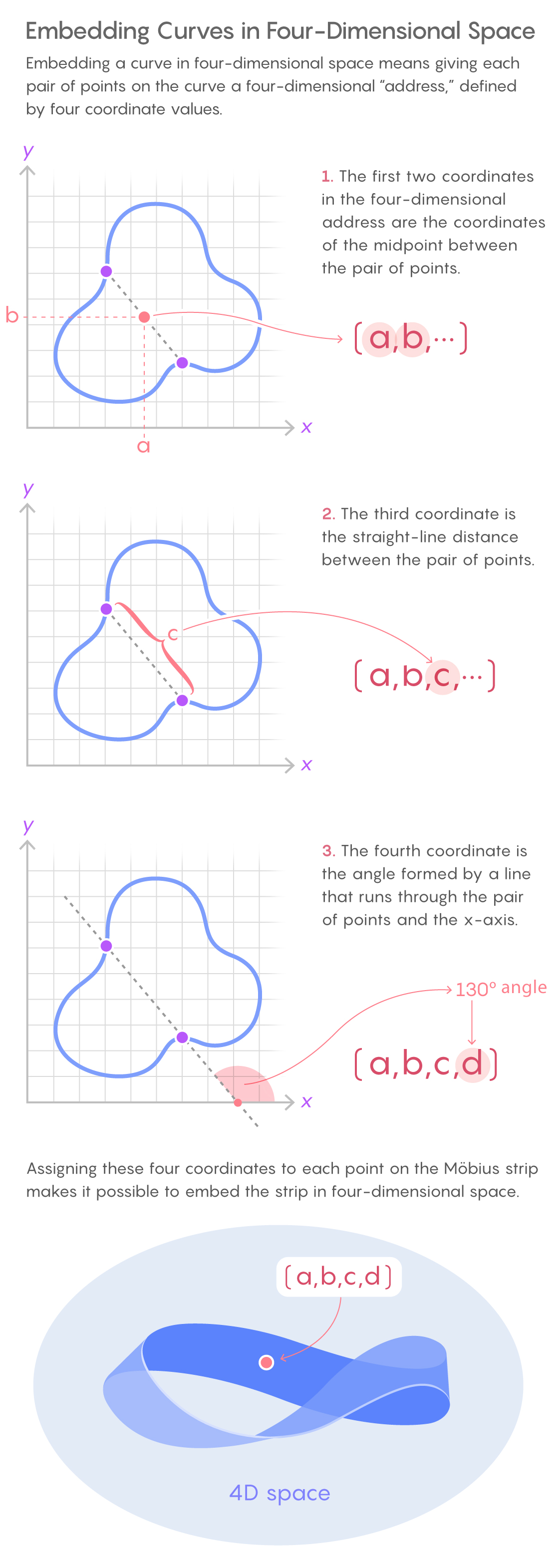
Hugelmeyer’s idea was to do something similar for the Möbius strip, but to embed it in four-dimensional space instead, where he could use features of four-dimensional geometry to prove the results he wanted about rectangles.
“Essentially, you’ve got your Möbius strip, and for each point on it you’re going to give it four coordinates. You give each point a kind of address in four-dimensional space,” said Lobb.
Hugelmeyer created these addresses in a way that would turn out to be particularly useful for the overall goal of finding rectangles on a curve. As with a postal address, you can think of him assigning each point on the curve a state, a city, a street name and a street number.
To do this, he began with a given point on the Möbius strip and looked at the two points on the original closed curve it represented. Then he found the midpoint of that pair of points and determined its x and y coordinates. Those were the first two values in the four-dimensional address (think of them as the state and city).
Next, he measured the straight-line distance between the two original points on the curve. That length became the third value in the four-dimensional address (think of this as the street name). Finally, he calculated the angle formed where a line through the two original points meets the x-axis. That angle became the fourth value in the four-dimensional address (think of this as the street number). These four values effectively tell you everything about the pair of points on the curve.
Samuel Velasco/Quanta Magazine
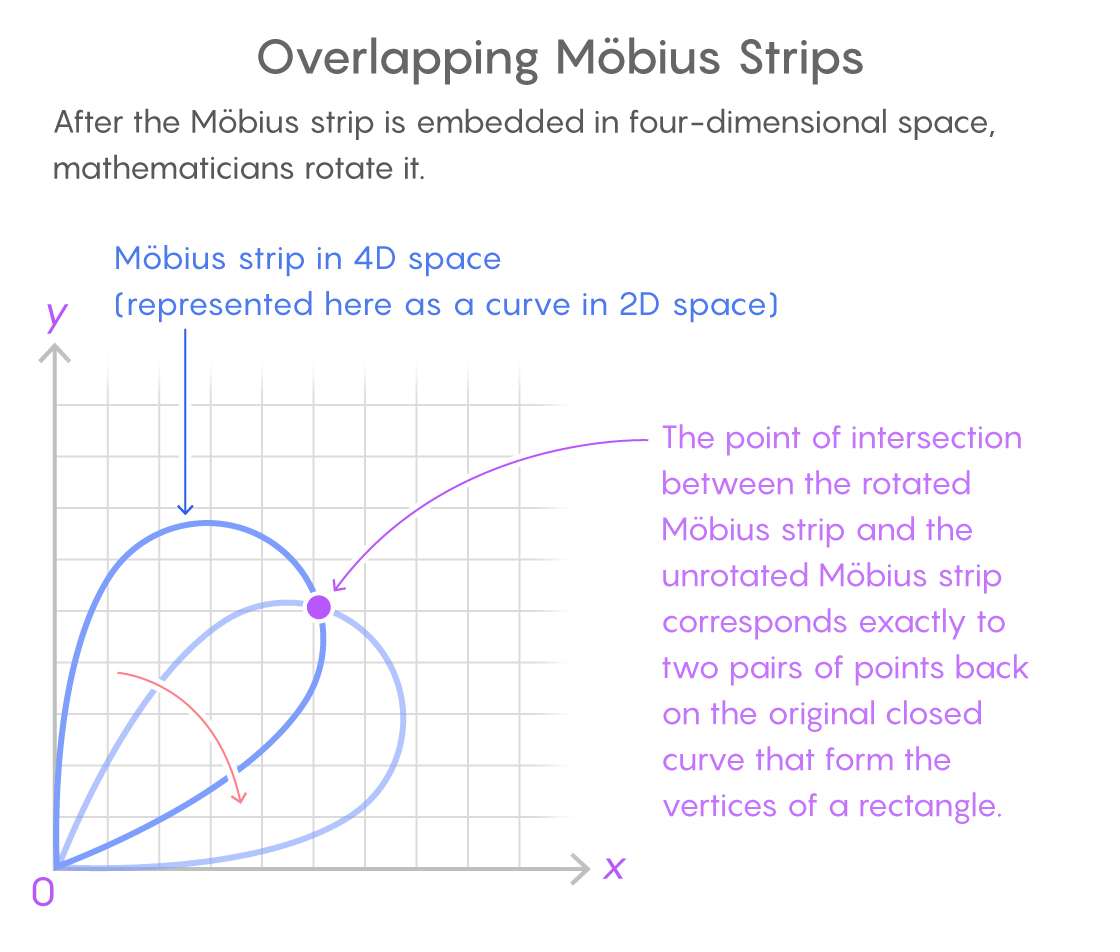
The exercise might seem complicated, but it paid quick dividends for Hugelmeyer. He took the embedded Möbius strip and rotated it, the way you could imagine holding a block in front of you and twisting it a bit to the left. The rotated Möbius strip was offset from the original, so the two copies intersected each other. (Because the rotation takes place in four-dimensional space, the exact way the two copies of the Möbius strip overlap is hard to visualize, but it’s mathematically easy to access.)
This intersection was critical. Wherever the two copies of the Möbius strip overlapped, you would find two pairs of points back on the original closed curve that formed the four vertices of a rectangle.
Why?
First, remember that a rectangle can be thought of as two pairs of points that share a midpoint and are an equal distance apart. This is exactly the information encoded in the first three values of the four-dimensional address assigned to each point on the embedded Möbius strip.
Second, it’s possible to rotate the Möbius strip in four-dimensional space so that you only change one of the coordinates in each point’s four-coordinate address — like changing the street numbers of all the houses on a block, but leaving the street name, city and state unchanged. (For a more geometric example, think about how holding a block in front of you and shifting it to the right only changes its x coordinates, not the y and z coordinates.)
Samuel Velasco/Quanta Magazine
Hugelmeyer explained how to rotate the Möbius strip in four-dimensional space so that the two coordinates encoding the midpoint between pairs of points remained the same, as did the coordinate encoding the distance between pairs of points. The rotation only changed the last coordinate — the one encoding information about the angle of the line segment between the pairs of points.
As a result, the intersection between the rotated copy of the Möbius strip and the original corresponded exactly to two distinct pairs of points back on the closed curve that had the same midpoint and were the same distance apart. Which is to say, the intersection point corresponded exactly to the four vertices of a rectangle on the curve.
This strategy, of using an intersection between two spaces to find the points you’re looking for, has long been used in work on the square and rectangular peg problems.
“Where those [spaces] intersect is where you have the thing you’re looking for,” said Denne. “All of these proofs in the history of the square peg problem, a lot of them have that idea.”
Hugelmeyer used the intersection strategy in a four-dimensional setting and got more out of it than anyone before him. The Möbius strip can be rotated by any angle between 0 and 360 degrees, and he proved that one-third of those rotations yield an intersection between the original and the rotated copy. This fact turns out to be equivalent to saying that on a closed curve, you can find rectangles with one-third of all possible aspect ratios.
“Credit to Cole for realizing that you should think about placing the Möbius strip in four-dimensional space and having four-dimensional techniques at your disposal,” said Greene.
At the same time, Hugelmeyer’s result was provocative: If four-dimensional space was such a useful way to attack the problem, why would it only be useful for one-third of all rectangles?
“You should be able to get the other two-thirds, for goodness’ sake,” Greene said. “But how?”
Keep It Symplectic
Even before they were locked down by the pandemic, Greene and Lobb had been interested in the rectangular peg problem. In February, Lobb hosted a conference at the Okinawa Institute of Science and Technology that Greene attended. The two spent a couple of days talking about the problem. Afterward, they continued their conversation during a week of sightseeing in Tokyo.
“We didn’t stop talking about the problem,” Lobb said. “We were going to restaurants, cafes, museums, and every now and again we’d have a thought about the problem.”
They continued their conversation even after they were confined to their respective homes. Their hope was to prove that every possible rotation of the Möbius strip yielded an intersection point — which is equivalent to proving you can find rectangles with all possible aspect ratios.
In mid-April, they came up with a strategy. It involved embedding the strip in a special version of four-dimensional space. With an ordinary embedding, you can place the embedded object any way you want. Think about embedding a one-dimensional closed loop in the two-dimensional plane. The number of ways you can do it are as limitless as the number of ways you can place a loop of string on a table.
But suppose the two-dimensional surface into which you’re going to embed the loop has some structure to it. Think, for example, about a map layered with arrows (called vectors) showing in which direction, and at what speed, the wind blows at each point on Earth. Now you have a two-dimensional surface with extra information, or structure, at each point.
You could then impose the restriction that the one-dimensional closed loop needs to be embedded on this map so that it always follows the direction of the arrows over which it’s embedded.
“Your constraint is you’re trying to put a curve in that follows those vectors,” Schwartz said. Now there are far fewer ways to place that loop of string.

Samuel Velasco/Quanta Magazine
Other types of geometric spaces make it possible to think about other types of constraints. The one that proved important in Greene and Lobb’s work is called a symplectic space.
This type of geometric setting first came up in the 19th century with the study of physical systems like orbiting planets. As a planet moves through three-dimensional space, its position is defined by three coordinates. But the Irish mathematician William Rowan Hamilton observed that at each point in a planet’s motion it is also possible to place a vector representing the planet’s momentum.
In the 1980s, a mathematician named Vladimir Arnold elaborated the mathematical study of symplectic geometry. He understood that geometric spaces with a symplectic structure intersect themselves under rotation more often than spaces without such a structure.
This was perfect for Greene and Lobb, who wanted to solve the rectangular peg problem for all aspect ratios by proving that a rotated copy of the parameterizing Möbius strip also intersects itself a lot. So they began trying to embed the two-dimensional Möbius strip in four-dimensional symplectic space.
“There was this pivotal insight to look at the problem from the perspective of symplectic geometry,” Greene said. “That was just a game changer.”
By late April, Greene and Lobb had determined that it was possible to embed the Möbius strip in four-dimensional symplectic space in a way that conformed to the structure of the space. With that done, they could start to use the tools of symplectic geometry — many of which bear directly on the question of how spaces intersect themselves.
“If you can make the [Möbius strip] follow symplectic rules, you get to make use of some symplectic theorems,” Lobb said.
Greene and Lobb were confident at this point that they could improve on Hugelmeyer’s result — meaning they could prove that more than one-third of all rotations produce an intersection. This in turn would mean that rectangles with more than one-third of all aspect ratios can be found as points on any closed curve.
“It was clear something was going to happen once we had this idea,” Lobb said.
But their result was more sweeping — and came much faster — than they’d anticipated. And the reason for that had to do with a quirky mathematical object called a Klein bottle, which had an important property when considered in the context of symplectic geometry.
The Klein Bottle Connection
The Klein bottle is a two-dimensional surface that looks like a modernist water pitcher. Like the Möbius strip, it only has one side, and you can actually make one by gluing together two Möbius strips. Any Klein bottle you could make and place on your desk, as many mathematicians do, crosses through itself. There is no way to embed the Klein bottle in three-dimensional space so that it doesn’t intersect itself.
“The Klein bottle is supposed to be a surface, but the handle, to get from the outside to the inside, has to crash through the bottle,” Schwartz said.
That isn’t always the case, though. In four-dimensional space, it is possible to embed the Klein bottle so that it doesn’t intersect itself. The fourth dimension provides extra room to maneuver that allows the Klein bottle to avoid itself. It’s similar to how two people walking toward each other on a one-dimensional line can’t help but collide, but two people approaching each other on a two-dimensional floor can easily swerve out of the way.

Samuel Velasco/Quanta Magazine
In May, Greene and Lobb happened to remember an interesting fact about the Klein bottle: It’s impossible to embed in four-dimensional symplectic space so that it doesn’t intersect itself. In other words, there’s no such thing as a nonintersecting Klein bottle that also conforms to the special rules of symplectic space. This fact was the key to the proof. “It was the magic bullet,” Greene said.
Here’s why. Greene and Lobb had already demonstrated that it’s possible to embed the Möbius strip in four-dimensional symplectic space in a way that follows the rules of the space. What they really wanted to know was whether every rotation of the Möbius strip intersects the original copy.
Well, two Möbius strips that intersect each other are equivalent to a Klein bottle, which intersects itself in this type of space. And if you rotate a Möbius strip so that the rotated copy doesn’t intersect the original copy, in essence you’ve produced a Klein bottle that doesn’t intersect itself. But such a Klein bottle is impossible in four-dimensional symplectic space. Therefore, every possible rotation of the embedded Möbius strip must also intersect itself — meaning every closed, smooth curve must contain sets of four points that can be joined together to form rectangles of all aspect ratios.
The conclusion, in the end, arrived like an avalanche.
“It is like setup, setup, setup, and then the hammer lands and the proof is done,” Denne said.
Greene and Lobb’s proof is a good example of how solving a problem often hinges on finding the right light in which to consider it. Generations of mathematicians failed to get a handle on this version of the rectangular peg problem because they tried to solve it in more traditional geometric settings. Once Greene and Lobb moved it into the symplectic world, the problem gave way with a whisper.
“These problems that were being thrown around in the 1910s and 1920s, they didn’t have the right framework to think about them,” Greene said. “What we’re realizing now is that they’re really hidden incarnations of symplectic phenomena.”
This article was reprinted on Wired.com.