How to Design (or at Least Model) Mixed Dog Breeds

James Round for Quanta Magazine
Introduction
Our June Insights puzzle featured a designer puppy named Dax who is a “Pomsky,” combining a Siberian husky’s handsome wolflike face with the size and fluffiness of a Pomeranian. When humans breed such combinations of two different purebred dog lines, they hope to produce offspring that have an admixture of the visual form, temperament and other characteristics — the phenotype— of both breeds. Is there a way to quantify what this proportion is exactly? You could assign a weight to every possible phenotypic characteristic you can think of and add them up, but such a weighting would be far too subjective. Instead, breeders focus on the genotype and carry out a straightforward calculation to figure out the proportion of genetic material contributed by each ancestral line. This mathematical exercise gives an objective and seemingly precise number for the genetic contribution from each breed. But, as we shall see, when we examine how genetic material actually flows down through generations, it’s clear that even this process is far too tricky to be captured precisely in an individual case.
Puzzle 1
Dax is certified to be 56% Siberian husky and 44% Pomeranian. Given that a cross between two purebreds is nominally considered to have an equal genetic mixture of both breeds, how is Dax’s unusual genetic makeup produced? What is the smallest number of generations needed to produce his genetic makeup to the nearest percentage point? (You must start with purebreds and cross their offspring only with each other or with purebred Poms or huskies.) If there is at least one purebred parent in every generation, are there more purebred huskies or Pomeranians in Dax’s ancestry?
Here is a possible family tree that can produce the 56-44 mixture.
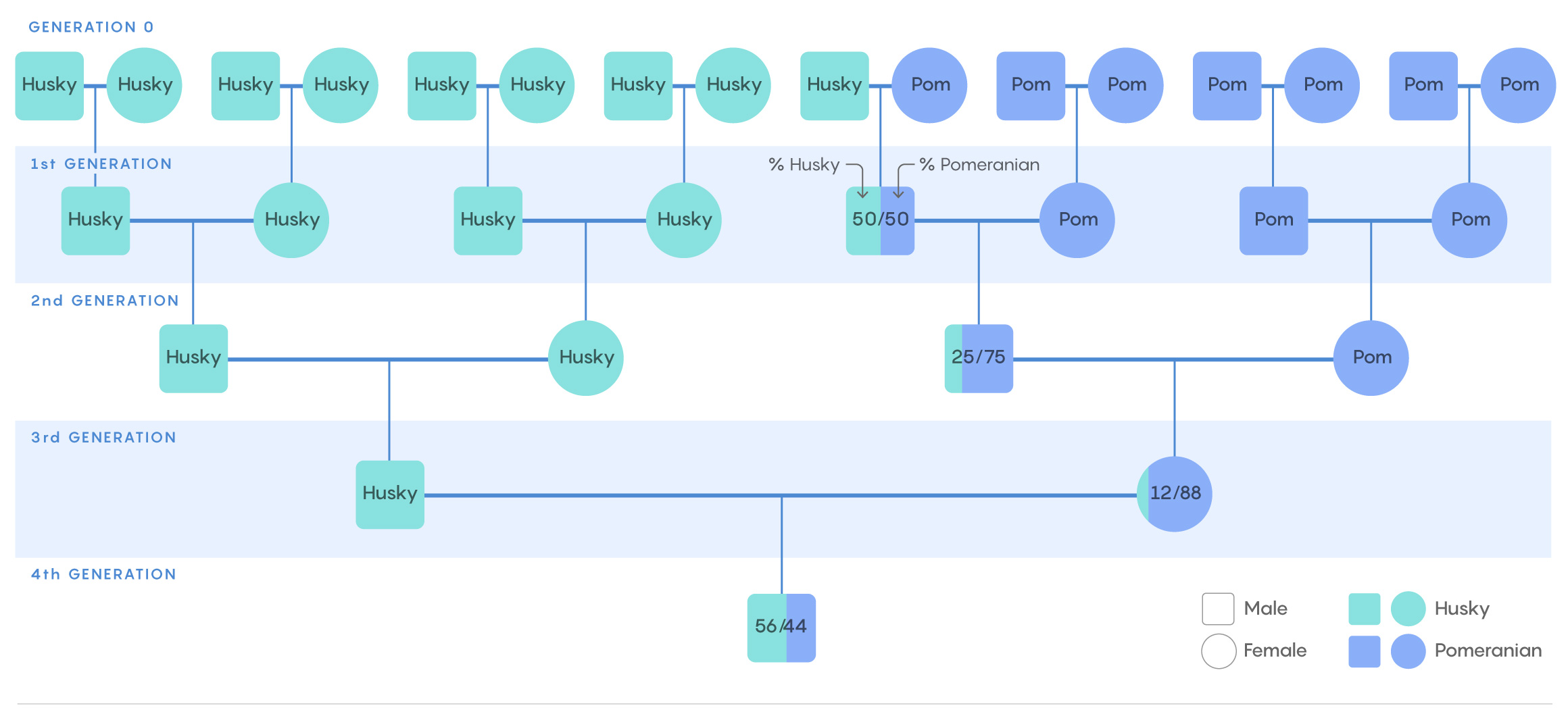
Samuel Velasco/Quanta Magazine
In the founding generation (generation 0), there are 16 dogs: eight males and eight females. None of the matings in any of the generations are between individuals with a common ancestor. So every founding individual contributes exactly the same amount of genetic material to all descendants belonging to the same generation as one another. For the fourth generation that fraction is 1/16. Since there are nine huskies and seven Poms to start with, our target individual, Dax, has to be 9/16 (56.25%) husky and 7/16 (43.75%) Pom.
This is a simple mathematical exercise using the powers of 2. If you breed for only one generation, you need only two purebred individuals, each of whom contributes one-half (50%) of their genetic material to the offspring. By choosing 0, 1 or 2 huskies in generation 0, you can produce individuals that are 0%, 50% or 100% husky.
If you can breed for two generations without allowing interbreeding, you start with four individuals contributing 1/4 each to the second generation, so you can produce 0%, 25%, 50%, 75% or 100% huskies by choosing the appropriate number of huskies and Poms in generation 0.
In the case of three generations, the “least count of huskyness” (or Pomness) at your disposal is 1/8 (12.5%). Thus, you can produce individuals with 0%, 12.5%, 25%, 37.5%, 50%, 62.5%, 75%, 87.5% or 100% of either breed.
With four generations, the least count is 1/16 (6.25%), and we can produce the required 56-44 proportion by doing a 9-7 split in generation 0.
Of course, since Dax is more than 50% husky, there have to be more purebred huskies than Poms in the entire family tree, and sure enough, there are 16 huskies but only 11 Pomeranians. But if you look only at how the huskyness proportion of 56% is reached (eliminating extraneous purebred-purebred matings), it requires just two purebred huskies (one parent, contributing 50% huskyness and one great-great-grandparent contributing 6.25%), but three purebred Poms (one grandparent contributing 25% Pomness, one great-grandparent contributing 12.5% and one great-great-grandparent contributing 6.25%). To see this, look at the family tree but focus only on the mixed, non-purebred individuals. Since each parent has a genetic contribution of 50%, Dax’s immediate purebred parent (in generation 3) cannot be a Pom. It has to be a husky who mates with an individual who is 87.5% Pom. To raise the proportion of Pomness to this high level from a 50-50 cross breed in generation 1, we need two successive matings with purebred Poms in generations 1 and 2.
This puzzle and the next one were well solved by Douglas Felix, Ty Rex and Jonathan Vercruysse.
Puzzle 2
Suppose Dax had a cousin, Max, who was 60% husky and 40% Pomeranian. What is the smallest number of generations it would take to produce a dog like Max using the same rules as in Puzzle 1? In general, what is the smallest number of generations needed to produce a Pomsky with any given percentage of “huskyness” to the nearest integer?
Let’s tackle the second question first and use it to answer the first. In order to produce any given percentage of huskyness to the nearest integer, you need a contribution “least count” of less than 1% so that you don’t skip any integer. This means that you need more than 100 purebred individuals in the founding generation. The smallest power of 2 that’s greater than 100 is 27, which is 128. To get 60% huskiness, we need to find 60% of 128, which is 76.8, and select the closest integer to it, which is 77. With 77 huskies and 51 Poms in generation 0, we can produce an individual who is 77/128 = 60.16% husky. Since 77 is an odd number, we cannot reduce this fraction to have a lower power of 2 in the denominator, so 5 or 6 generations will not work.
To find out the number of generations needed to breed an individual with any percentage p of huskyness, construct a fraction with the integer closest to 128 × p/100 as the numerator and 128 as the denominator, and reduce the fraction to its simplest form. The denominator will be of the form 2n where n is the number of generations. This method was essentially the one described by Jonathan Vercruysse.
Note, however, that since 128 is more than 100, there are some integer percentages that can be produced in more than one way from 128 purebreds. Thus, to produce a husky percentage of 20, you can use either 26 (20.3%) or 25 (19.5%) huskies in generation 0. The former fraction can be reduced to 13/64 and therefore can be achieved in six generations, while the latter cannot. Thus, to be absolutely sure you have the fewest number of generations, we need to add one more step to your algorithm. If 128 × p/100 rounds to an odd integer, check whether the even integer you get by rounding in the other direction also yields the desired percentage. If it does, select the even number and reduce it to obtain the fewest number of generations.
Puzzle 3
The total quantity of genetic material in a genome can be measured by counting the number of DNA base pairs in it. All the cells of female dogs, except for egg cells, have two copies of each chromosome with a total of approximately 5 billion DNA base pairs. Of these, 50% go to each offspring through the egg. Female offspring receive an equal genetic contribution from their father’s sperm, including all the non-sex chromosomes and another X chromosome. For male offspring, however, the sperm carries the rest of the chromosomes and the Y chromosome, which has about 100 million fewer base pairs than the X chromosome. Based on this information, what proportion of their genome do male dogs actually inherit from their mother? How does this affect the answer to Puzzle 1?
As Jonathan Vercruysse explains, male dogs have 4.9 billion DNA base pairs, of which 2.4 billion base pairs come from the father.
Thus, male dogs have 2.5 billion base pairs (51%) from their mother and 49% from their father. This means that a male dog like Dax would have about 1% more huskyness than we previously calculated if his mother was a husky and 1% less huskyness if his father was a husky.
Since Dax is male, the previously described family tree would not give the required 56% huskyness but rather 57% if his mother is a husky or 55% if his father is a husky. To reach 56% huskyness, we will have to either target 55% or 57% using our previous technique.
The former is reachable in the sixth generation using the following calculation: 55% of 128 rounds down to 70, giving the fraction 70/128, which reduces to 35/64. 64 is 26. So in the 6th generation, Dax can reach 56% huskyness if his mother is a husky.
The fraction for 57% huskyness is 73/128, which cannot be reduced and will require seven generations.
This 1% deviation from 50% in the amount of genetic material inherited from a male’s mother and father applies within a single generation. But there’s another phenomenon — “meiotic recombination” — that causes a far greater disparity in the amount of genetic material that two siblings can inherit from their grandfather or grandmother. This is wonderfully explained by Ty Rex. The effect of this, as Ty Rex states, is that in humans, “two siblings, i.e., with the same parents, can share widely differing amounts of DNA: from as little as 37% to as much as 62%.” The same phenomenon exists in all mammals, though the spread may be somewhat smaller in dogs because they have many more pairs of chromosomes (39) than humans (23), which may dampen the effects of recombination somewhat.
What this means for Puzzle 1 is that the family tree we calculated (with the correction for maleness we made in Puzzle 3) does not guarantee that Dax, as an individual dog, will have the advertised husky-Pomeranian percentage split in reality. All we can say is that the average genetic endowment of a group of dogs bred in exactly the same way as Dax will come out to be 56% husky and 44% Pomeranian.
Yes, heredity is indeed far more subtle than we’d guess from the simple Mendelian mathematical rules we learned in school. Mendel’s genius lay in divining the simple foundational rules that enable us to begin thinking intelligently about heredity. But there is plenty of complexity that has to be added even if we consider the genotype alone. And we have not even touched on how the genotype creates the phenotype — how a single gene can orchestrate the development of a complex organ like the eye, while polygenic traits like height can be affected by hundreds of genes. Thus, a small number of genes on the Y chromosome can create maleness, which is a rather large phenotypic change, even though the father’s contribution to the male genotype is less than the mother’s, as we saw above.
Ty Rex also recommended the recent book She Has Her Mother’s Laugh by Carl Zimmer, which is about “the history and remarkable facts of heritability. Stories include ‘mosaics,’ and the mother for whom multiple DNA tests insisted she was not related to her own children!” Thank you for this enlightening discussion, Ty Rex.
Question 1
COVID-19 is known to be particularly devastating to the very old. The following data from the CDC gives the breakdown of about 70,000 COVID deaths in the U.S. by age group. It shows that people who are 85 or older are the most vulnerable. In this data, there were more males than females, although the ratio of male to female deaths was about 55:45, which is somewhat lower than in the rest of the world.
| Age Group | No. of Deaths |
| Under 1 | 3 |
| 1-4 | 2 |
| 5-14 | 7 |
| 15-24 | 76 |
| 25-34 | 463 |
| 35-44 | 1,186 |
| 45-54 | 3,338 |
| 55-64 | 8,312 |
| 65-74 | 14,447 |
| 75-84 | 18,621 |
| 85 and over | 22,543 |
However, as people get older, the number of years they can expect to live decreases. Which age group in the above table has lost the most years of life on account of COVID? Take a guess. In order to figure this out accurately, you have to use actuarial tables like this one, which shows that a 62-year-old man has an average life expectancy of another 20 years, while an 87-year-old can only expect to live another five years on average. Does the final answer surprise you?
Jonathan Vercruysse and Douglas Felix performed this calculation. The following is the number of years lost in each age range.
| Age Group | Years lost |
| Under 1 | 235 |
| 1-4 | 152 |
| 5-14 | 485 |
| 15-24 | 4,522 |
| 25-34 | 23,185 |
| 35-44 | 48,391 |
| 45-54 | 106,052 |
| 55-64 | 194,567 |
| 65-74 | 229,196 |
| 75-84 | 176, 762 |
| 85 and over | 108,055 |
It turns out that 65- to 74-year-olds have lost the most life years to COVID-19, but 55- to 64-year-olds and 75- to 84-year-olds come pretty close. What surprised me is that 45- to 54-year-olds have lost almost as many life years as the over-85 group. So the societal loss of person-years due to COVID-19 is as high in middle-aged people as it is in the very elderly! It’s definitely worth repeating: Stay safe, everyone!
For Question 2 of this column I presented a speculative hypothesis that attempted to explain why pandemics may have been responsible for the fact that mammals rely wholly on sexual reproduction, even though some reptiles can reproduce asexually. Based on this idea, I asked readers to discuss: Could pandemics be the reason that mammals reproduce sexually instead of asexually? Did pandemics give us sex?
I didn’t get much of a response, so perhaps this hypothesis needs to be sharpened and revisited another day.
I would like to award this month’s prizes to both Ty Rex and Jonathan Vercruysse. Congratulations, and thank you everyone for your contributions to this discussion.
See you next month for new Insights.



