How to Find Simple Treasures in Complex Numbers

For our first Insights puzzle of 2019, let’s go on a treasure hunt. To prepare you for this adventure, let me start by giving you a valuable thought to ponder: It is possible for anyone to understand that “imaginary” numbers (numbers that contain the seemingly nonsensical square root of minus 1) are actually as “real” as any other numbers given the right situation. If imaginary numbers have always seemed strange to you, prepare for a change in perspective. We are going to make imaginary numbers your real friends.

In the exclusive domain of positive and negative real numbers, of course, the root of a negative number has no meaning. However, think for a moment about negative numbers themselves: In the domain of counting, negative numbers have no meaning either. Over two millenniums ago, the Chinese realized that negative numbers (which they marked using beads of a different color)  could be used to express debts in monetary transactions. In the year 620, the Indian mathematician Brahmagupta formalized arithmetical operations for negative numbers using a special sign, much as we do today. But to many European mathematicians, negative numbers were unthinkable and were rejected in calculations until the mid-1700s! It was not until the 19th century that Western mathematicians finally and fully accepted negative numbers. What it takes to change any kind of number from “unthinkable” or “imaginary” to “real” is the redefinition and expansion of mathematical operations like addition and multiplication to work in a consistent way that is natural and useful in new situations. Today we have an easy familiarity with negative numbers everywhere. Beyond IOUs, we see them in GPS navigation coordinates, in temperature scales, in geographical latitudes, and even in sports, video games and game shows such as Jeopardy!

Negative numbers are of course, ubiquitous in mathematics now. In geometry, we use them to describe reverse directionality on the number line. In a similar way, imaginary and complex numbers (expressions of the form a + bi, where the real numbers a and b join the square root of minus 1, represented by the imaginary unit “i”) are no more unthinkable than negative numbers once were. They arise naturally from familiar numbers in many situations, giving rise to several real-world applications — in electrical engineering and quantum mechanics, for instance. Complex numbers and their descendants (such as quaternions and octonions) map real features of the physical world, as Patrick Honner explained in the recent Quanta math column “The (Imaginary) Numbers at the Edge of Reality.” But for most people, the term “imaginary” still gives these numbers an aura of strangeness, a feeling that they are mere mathematical tools, but somehow do not possess the naturalness or legitimacy to be called true numbers.

Not so! To help see this, ponder the following question: Imagine that you have a blank paper with a central point or origin marked on it. Your challenge is to label every point on this plane with a single number that describes its position. Additionally, you should be able to add and multiply these numbers in natural and consistent ways that can actually help you calculate two-dimensional relationships. No fair using coordinate geometry — every point must be delineated by one single arithmetically manipulable number only. If you think about this deeply, you will realize that the only solution that works is to invent or use complex numbers (as Jean-Robert Argand and Caspar Wessel independently did around 1800).

In this solution, known as the Argand (or complex) plane, the location of every point is the sum of a real part for its horizontal distance and an imaginary part for its vertical distance from the origin. This allows you to do all of coordinate geometry and vectors using single numbers. A point that is, say, 4 units to the right of the origin and 3 units above it is assigned the single coordinate 4 + 3i. This composite number can actually be manipulated as a single entity using the familiar rules of addition and multiplication, resulting in a completely natural generalization of the number line from one to two dimensions. Familiar operations that work on the number line also work on the complex plane, but now yield new functionality and new insights. Here’s how it works:

Addition: To add two numbers such as 2 + 3 on the number line, you move 2 units from the origin, and then another 3, to reach 5.

If a number is negative, just move in the opposite direction: 2 + –3 = –1.

In the complex plane, you can go to 2 + 2i and then move another 3 + 3i to reach 5 + 5i, which lies along the same line, as before.

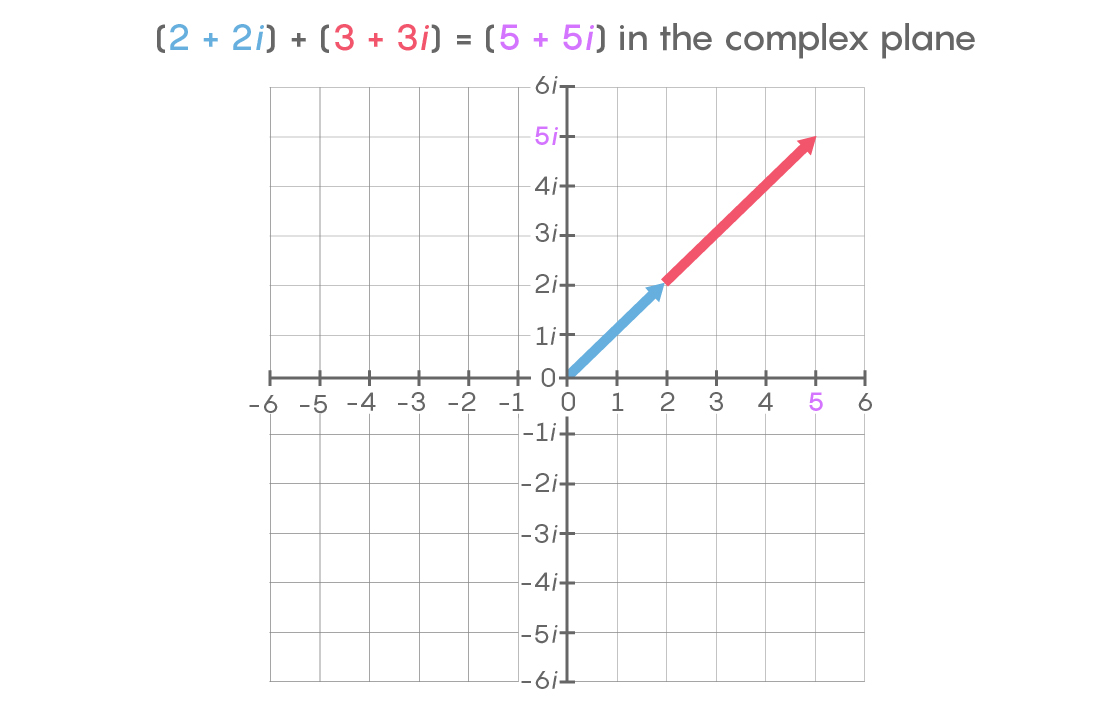
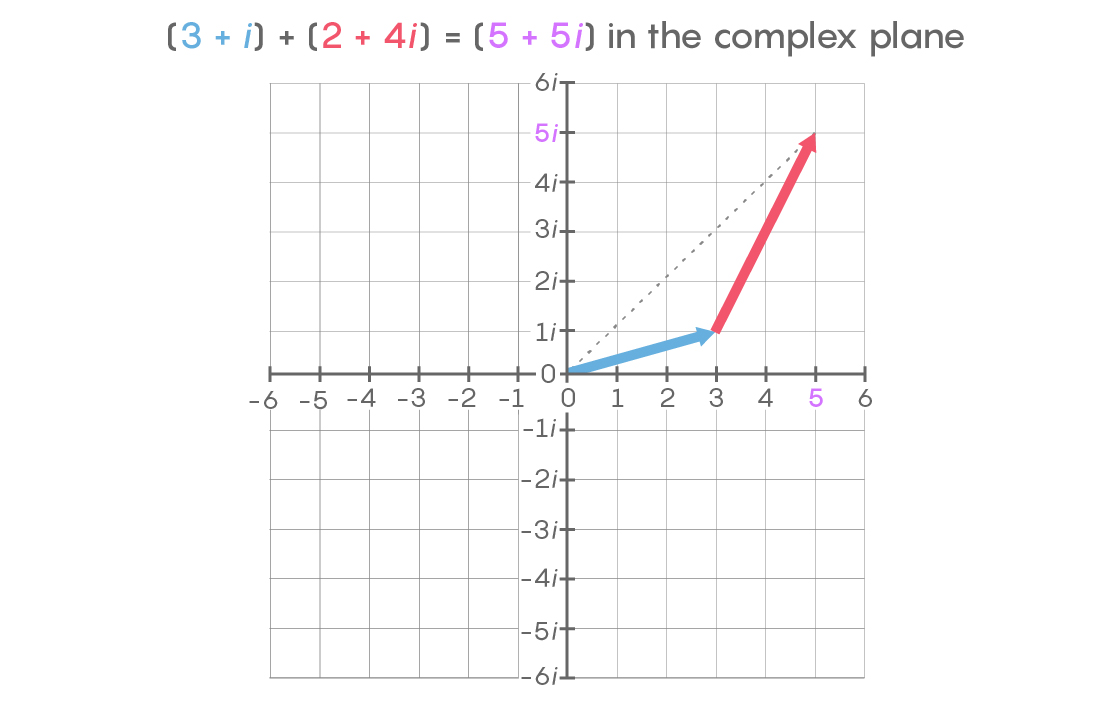
But if you travel to 3 + i and then go another 2 + 4i, you will end up at a point that is the sum of the two but does not lie along the same line as either: 5+ 5i. This complex number addition is exactly equivalent in magnitude and direction to the addition of vectors in calculating the “parallelogram of forces” from high school physics and in measuring the sides of triangles.

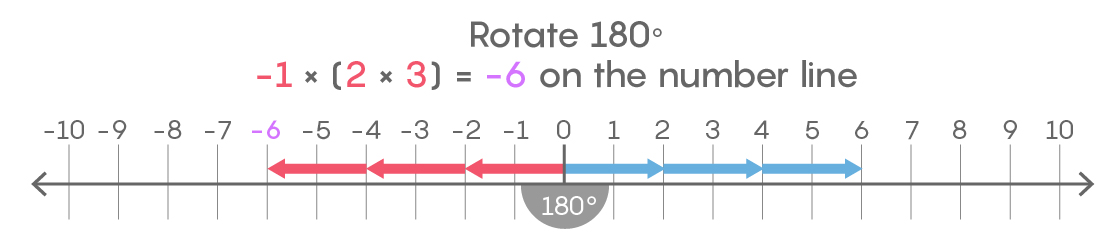
Multiplication: To multiply 2 and 3 on the number line, you simply move 2 units from the origin 3 times.

The same process works in the complex plane for multiplication by a positive number: 3 times 2 + 2i = 6 + 6i. To multiply by a negative number on the number line requires you to first multiply by the positive part as before, and then multiply by –1, which rotates things 180 degrees around the origin. Thus, if you move 2 units from the origin, multiply by 3 to reach 6 and then rotate 180 degrees around the origin, you reach –6.

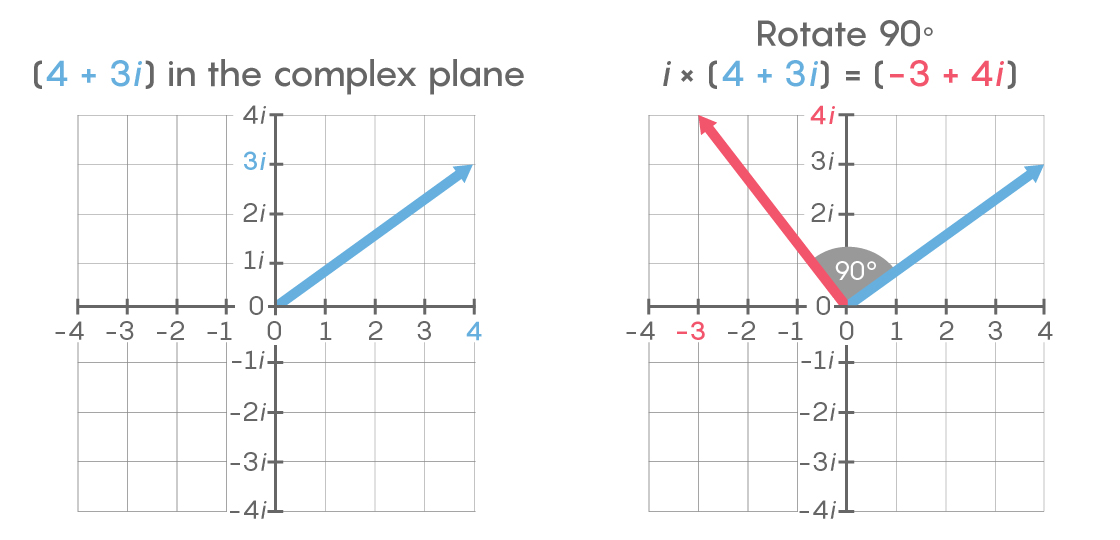
What happens in two dimensions if you rotate just one right angle (90 degrees)? If turning two right angles is the same as multiplying by –1, then turning a single right angle requires multiplying by a number that gives us –1 when we multiply by it twice. This is the square root of –1, which, as we now know, is i. By convention, rotating through a right angle counterclockwise is considered multiplication by i, whereas doing it clockwise is multiplying by –i. This works for all points on the plane. Thus, if you start at 4 + 3i and turn through one right angle counterclockwise, you will find yourself at i × (4 + 3i) = 4i + 3i² = –3 + 4i.

Finding the midpoint: To find the midpoint between two points on the number line, all you have to do is find their mean. The midpoint of the line joining 4 + 3i and 2 + 5i is, simply, (4 + 2 + 3i + 5i) / 2 = 3 + 4i.

With these preliminaries out of the way, let’s find buried pirate treasure! Below are instructions to find two treasures. The first of these problems can be solved by classical or coordinate geometry, but the complex number solution is simpler (go figure!). This first puzzle is a variant of one originally described by the famed nuclear physicist George Gamow in a delightful book called One, Two, Three…Infinity: Facts and Speculations of Science, originally published in 1947. In stating this puzzle, I have retained Gamow’s words to show his puckish sense of humor, but have made small modifications to make it current, and, of course, to yield a different answer.

Treasure One

There was a young and adventurous man who found among his great-grandfather’s papers a piece of parchment that revealed the location of a hidden treasure. The instructions read:

“Sail to ______ north latitude and ______ west longitude where thou wilt find a deserted island. (Actual coordinates have been omitted so as not to give away the secret and cause a gold rush among Quanta readers.) There lieth a large meadow on the north shore of the island where standeth a lonely oak and a lonely pine. (Tree names have been changed for the same reason — obviously there would be different varieties on a tropical island.)  There thou wilt see also an old gallows on which we once were wont to hang traitors. Start thou from the gallows and walk to the oak counting thy steps. At the oak thou must turn right by a right angle and take exactly three times as many steps as thou just took to reach the tree. Put here a spike into the ground. Now must thou return to the gallows and walk to the pine counting thy steps. At the pine thou must turn left by a right angle and again take exactly three times as many steps as thou took to reach the tree. Put thou another spike into the ground. Dig halfway between the spikes; the treasure is there.”

The young man charted a ship and sailed to the South Seas, where he found the island, the field, the oak and the pine. But to his great sorrow, the gallows was gone. Too much time had passed since the document had been written; the elements had disintegrated the wood and returned it to the soil, leaving no trace even where it once had stood. The young man, in an angry frenzy, began to dig at random, but the island was too big. So he sailed back empty-handed. The treasure is probably still there.

A sad story, but what is sadder is the fact that the fellow might have had the treasure, if only he had known a bit about mathematics, and specifically the use of imaginary numbers. Can you find the treasure for him?

Our second treasure is equally full of precious gems and was buried on the same island by a 19th-century pirate ship navigator who was an accomplished mathematician and amateur poet. Apparently, he had once written an advanced commentary on Euler’s immortal formula: e^iπ  =  –1. Needless to say, the instructions to find the treasure were in the form of an amazingly brief poem — of sorts. You might even need some help from Euler’s formula to find it! AAARRGH!

Treasure Two

An eye for an eye and a tooth for a tooth

Recall thee the pirate creed. Forsooth!

At the lonely oak we rounded traitors, aye!

Then took them to the pine, minus eye.

Dead men’s chests swelled the treasure so big!

Ponder ye the creed: eye to the eye! Now go dig.

Happy puzzling!

Editor’s note: The reader who submits the most interesting, creative or insightful solution (as judged by the columnist) in the comments section will receive a Quanta Magazine T-shirt or one of the two new Quanta books, Alice and Bob Meet the Wall of Fire or The Prime Number Conspiracy (winner’s choice). And if you’d like to suggest a favorite puzzle for a future Insights column, submit it as a comment below, clearly marked “NEW PUZZLE SUGGESTION.” (It will not appear online, so solutions to the puzzle above should be submitted separately.)

Note that we may hold comments for the first day or two to allow for independent contributions by readers.

Update: The solution has been published here.