The (Imaginary) Numbers at the Edge of Reality

Have you ever sat in a math classroom and wondered, “When will I ever use this?” You might have asked yourself this question when you first encountered “imaginary” numbers, and with good reason: What could be less practical than a number described as imaginary?

But imaginary numbers, and the complex numbers they help define, turn out to be incredibly useful. They have a far-reaching impact in physics, engineering, number theory and geometry. And they are the first step into a world of strange number systems, some of which are being proposed as models of the mysterious relationships underlying our physical world. Let’s take a look at how these unfamiliar numbers are rooted in the numbers we know, but at the same time, are unlike anything we have imagined.

The “real numbers” are some of our most familiar mathematical objects: They are all the numbers that can be represented in decimal notation, like 5, 8.2, -13.712, 0, 10.33333… and $latex \pi \approx$ 3.141592…. We can add, subtract, multiply and divide real numbers, and we use them to answer questions both in classrooms and in our everyday lives. But the real numbers aren’t enough to solve all our math problems.

In the 1500s, the master equation solver Girolamo Cardano was trying to solve polynomial equations. He had no trouble solving equations like $latex x^2-8x+12=0 $, because it was easy to find two numbers whose sum was 8 and whose product was 12: namely, 2 and 6. This meant $latex x^2-8x+12$ could be factored as $latex (x-2)(x-6)$, and expressing this polynomial as a product of two factors made solving the equation $latex x^2-8x+12=0$ easy.

But it wasn’t so easy to do this for equations like $latex x^2-3x+10=0$. Finding two numbers that add to 3 and multiply to 10 seems an impossible challenge. If the product of the two numbers is positive, they must have the same sign, and since their sum is positive, this means they must both be positive. But if two positive numbers add up to 3, they must both be less than 3, which means their product will be less than 3 × 3 = 9. There doesn’t seem to be a way to make this work.

Yet Cardano discovered that he could make it work, if he allowed himself to consider numbers that involved $latex \sqrt{-1}$, the square root of –1. It was a disturbing discovery. The square root of a number k, or $latex \sqrt{k}$, is the number that when multiplied by itself produces k. Now, when you square a real number, the result can never be negative: for example, 3 × 3 = 9, (-1.2) × (-1.2) = 1.44 and 0 × 0 = 0. This means no real number multiplied by itself could equal –1: Cardano was using $latex \sqrt{-1}$ to solve his real number equations, but $latex \sqrt{-1}$ isn’t itself a real number.

Cardano treated these non-real, or “imaginary,” numbers hesitantly, even describing the arithmetic he did with them as useless. But he was surprised to find that they obeyed many of the same rules that real numbers do. And although it took a while, Cardano’s reluctant use of $latex \sqrt{-1}$ led to the development of the “complex numbers,” a powerful and productive extension of the real numbers.

Complex numbers are made up of a real part and an imaginary part. They have the form a + bi, where a and b are both real numbers, and $latex i=\sqrt{-1}$, also known as the “imaginary unit.” They may seem strange at first, but we quickly find that we can add, subtract, multiply and divide complex numbers just as we do with real numbers.

To add and subtract complex numbers, you just combine the real parts and the imaginary parts, like this:

(5 + 3i) + (2 + 8i) = (5 + 2) + (3 + 8)i = 7 + 11i

This is similar to combining “like terms” when you add polynomials together:

(3x + 2) + (5x + 7) = 8x + 9

Multiplication of complex numbers is done using the same “distributive property” we use with real numbers. The distributive property tells us how multiplication and addition work together: For example, when you multiply 2 and (5 + i), you distribute the 2 over the sum of 5 and i:

2 × (5 + i) = 2 × 5 + 2 × i
           = 10 + 2i

To multiply 2 + 3i and 5 + i, you just apply the distributive property twice. Here, the multiplication by (5 + i) is first distributed over the sum of 2 and 3i. That is, $latex (2+3i)\times(5+i)$:

$latex \begin{align*}
&= 2 × (5 + i) + 3i × (5 + i)\\
&= 10+2i+15i+3i^2\\
&= 10+17i+3i^2
\end{align*}$

Notice that our answer, $latex 10+17i+3i^2$, doesn’t have the form a + bi. Is this really a complex number, or is it something else? Here’s where we use the fact that $latex i^2=-1$.

$latex \begin{align*}
(2+3i)\times(5+i) &= 10+17i+3i^2\\
&= 10+17i+3(-1)\\
&= 10+17i-3\\
&= 7+17i
\end{align*}$

Since we can write $latex 10+17i+3i^2$ in the form a + bi, we know it is indeed a complex number. This illustrates the property of “closure”: When you multiply two complex numbers, you get another complex number. You don’t get something else.

Multiplication of complex numbers is even “commutative”: This means when you multiply two complex numbers in either order, the result is the same. For instance, you can verify that (5 + i) × (2 + 3i) = 7 + 17i. We often take for granted that multiplication of real numbers is commutative — for example, that 5 × 4 = 4 × 5 — but as we shall see later, this important fact doesn’t hold for every number system.

So we can multiply complex numbers, but how do we divide them? The key is understanding the relationship between division and multiplication.

I often tell students that there is no such thing as division: There is only multiplication by the reciprocal. When we see the expression $latex \frac{10}{2}$, we usually think “10 divided by 2,” but we can also think of this as $latex 10\times\frac{1}{2}$, or “10 multiplied by the reciprocal of 2.”

The reciprocal of a real, non-zero number a is written $latex \frac{1}{a}$, and it is the unique number that, when multiplied by a, produces 1. The reciprocal of 2 is $latex \frac{1}{2}$, since $latex 2\times\frac{1}{2}=1$. And it’s important to note that $latex \frac{1}{2}$ is a real number — you can write it as 0.5 if you need to convince yourself.

Now this may seem like an unnecessarily complicated approach to division, but it pays off when you start to think about numbers like$latex \frac{1}{i}$. The meaning of “1 divided by i” may not be immediately clear, but “the reciprocal of i” is the number you multiply with i to get 1. And it may be a little surprising that this number is –i!

i × (–i) = – (i × i) = – (–1) = 1

Using the fact that i × i = –1, and some other important properties of real and complex numbers (that let us bring the negative sign out in front of the expression), we see that i × (–i) = 1, and so –i really is the reciprocal of i. This means that if we ever want to divide a number by i, we can just multiply it by –i instead.

For other complex numbers, the arithmetic may get a little harder, but the reciprocal idea still works. For example, to compute $latex \frac{1+2i}{3+4i}$ we need to find the reciprocal of 3 + 4i, and to do that we’ll use a trick involving the “conjugate” of a complex number — that is, the number you get when you switch the sign of its imaginary part.

Notice what happens when we multiply the complex number 3 + 4i by its conjugate 3 – 4i. That is, $latex (3+4i)\times(3-4i)$:

$latex \begin{align*}
&= 3\times(3-4i)+4i\times(3-4i)\\
&=3\times 3-3\times 4i+4i\times 3-4i\times 4i\\
&= 9-12i+12i-16i^2\\
&= 9-16i^2\\
&= 9+16\\
&= 25
\end{align*}$

The product of the complex number and its conjugate is a real number! This is true in general, since $latex (a+bi) \times (a-bi)=a^2+b^2$ and a and b are always real numbers.

This property of conjugates helps us compute the reciprocal of any complex number. Since (3 + 4i) × (3–4i) = 25, we divide both sides of the equation by 25 and do some algebra:

$latex (3+4i) \times (3-4i)=25$

$latex \frac{(3+4i) \times (3-4i)}{25}=\frac{25}{25}$

$latex \frac{(3+4i) \times (3-4i)}{25}=1$

$latex (3+4i) \times \frac{(3-4i)}{25}=1$

Since  $latex (3+4i)$ and $latex \frac{(3-4i)}{25}$ multiply to 1, we know  $latex \frac{(3-4i)}{25}$ is the reciprocal of $latex (3+4i)$. When we want to divide by $latex (3+4i)$, we just multiply instead by $latex \frac{(3-4i)}{25}$. So to compute  $latex \frac{1+2i}{3+4i}$, we multiply:

$latex \frac{1+2i}{3+4i}=(1+2i)\times\frac{(3-4i)}{25}=\frac{11+2i}{25}$

The introduction of this one new non-real number — i, the imaginary unit — launched an entirely new mathematical world to explore. It is a strange world, where squares can be negative, but one whose structure is very similar to the real numbers we are so familiar with. And this extension to the real numbers was just the beginning.

In 1843, William Rowan Hamilton imagined a world in which there were many distinct “imaginary units,” and in doing so discovered the quaternions. The quaternions are structured like the complex numbers, but with additional square roots of –1, which Hamilton called j and k. Every quaternion has the form a + bi + cj +dk, where a, b, c and d are real numbers, and $latex i^2=j^2=k^2=-1$. You might think anyone can invent a new number system, but it’s important to ask if it will have the structures and properties we want. For instance, will the system be closed under multiplication? Will we be able to divide?

To ensure the quaternions had these properties, Hamilton had to figure out what to do about i × j. All quaternions need to look like a + bi + cj +dk, and i × j doesn’t. We ran into a similar problem when we first multiplied two complex numbers: Our initial result had an i × i term in it, which didn’t seem to fit. Luckily, we could use the fact that $latex i^2=-1$ to put the number in its proper form. But what can be done with i × j?

Hamilton himself struggled to understand this product, and when the moment of inspiration finally came, he carved his insight into the stone of the bridge he was crossing:

$latex i^2=j^2=k^2=i\times j\times k=-1$

People from all over world still visit Broome Bridge in Dublin to share in this moment of mathematical discovery.

Hamilton’s famous relationship between the imaginary units i, j and k allows us to multiply and divide quaternions and get the results we mostly expect. Let’s see how this resolves the question of what i × j should be.

Starting with i × j × k = –1, we multiply both sides of the equation (on their right sides) by k and simplify.

$latex \begin{align*}
i\times j\times k &= -1\\
(i\times j\times k)\times k &= -1\times k\\
(i\times j)\times(k\times k) &= -k\\
(i\times j)\times(-1) &= -k\\
-(i\times j) &= -k\\
i\times j &= k
\end{align*}$

From Hamilton’s relationship, we see that i × j = k . Here we are using the fact that  k × k = –1 along with other properties, including the “associative property” of multiplication, which says that, when multiplying more than two things together, you can choose which pair to multiply first. This is another property we take for granted with the real numbers — for example, (2 × 3) × 10 = 2 × (3 × 10) — and as with commutativity, we will see it doesn’t always hold for every number system.

The other products can be derived in a similar way, and so we get a multiplication table of imaginary units that looks like this:

i × j = k                    j × k = i                    k × i = j
j × i = –k                  k × j = –i                  i × k = –j

These quaternion multiplication rules can be represented in the following diagram:

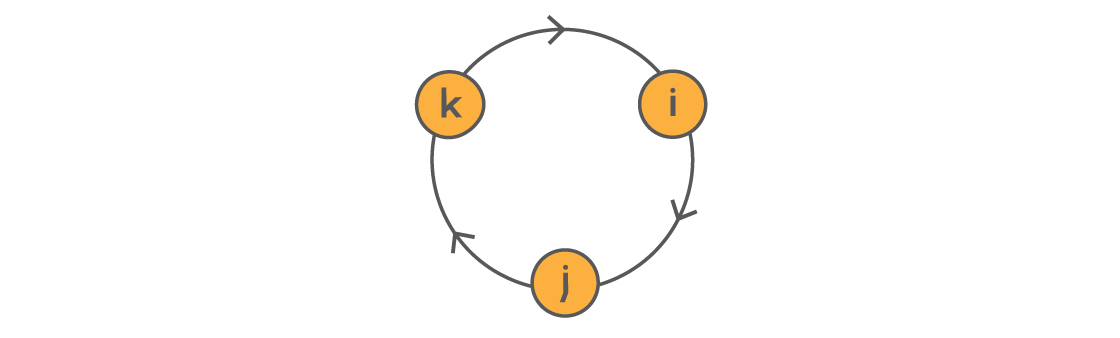
Here, moving around the circle in the direction of the arrows gives you the appropriate product (i × j = k), and moving in the opposite direction introduces a factor of –1 (ex. j × i = –k). Notice this means that, unlike with the real and complex numbers, multiplication of quaternions is not commutative. (This is why we had to multiply both sides of the equation i × j × k = –1 above by k on their right sides.) Multiplying two quaternions in different orders may produce different results!

$latex i\times j=k\neq-k=j\times i$

To get the kind of structure we want in the quaternions, we have to abandon the commutativity of multiplication. This is a real loss: Commutativity is a kind of algebraic symmetry, and symmetry is always a useful property in mathematical structures. But with these relationships in place, we gain a system where we can add, subtract, multiply and divide much as we did with complex numbers.

To add and subtract quaternions, we collect like terms as before. To multiply we still use the distributive property: It just requires a little more distributing. And to divide quaternions, we still use the idea of the conjugate to find the reciprocal, because just as with complex numbers, the product of any quaternion with its conjugate is a real number.

$latex (a+bi+cj+dk)\times(a-bi-cj-dk)=$
$latexa^2+b^2+c^2+d^2$

For example, if we want to divide by the quaternion 1 + i + j + k, we use the fact that (1 + i + j + k)(1 – i – j – k) = 4, which allows us to find the reciprocal of 1 + i + j + k, namely:

$latex \frac{1}{1+i+j+k}=\frac{1-i-j-k}{4}$

Thus, the quaternions are an extension of the complex numbers where we can add, subtract, multiply and divide. And like the complex numbers, the quaternions are surprisingly useful: They can be used to model the rotation of three-dimensional space, which makes them invaluable in rendering digital landscapes and spherical video, and in positioning and orienting objects like spaceships and cellphones in our three-dimensional world.

These extensions beyond the real numbers continue still with the eight-dimensional octonions, an even stranger number system discovered by Hamilton’s colleagues that has seven imaginary units. Just as in all the other numbers systems we’ve seen, you can add, subtract, multiply and divide octonions. And just as with the quaternions, we need some special rules to govern how to multiply all the imaginary units. Here they are, represented graphically in a diagram known as the “Fano plane”:

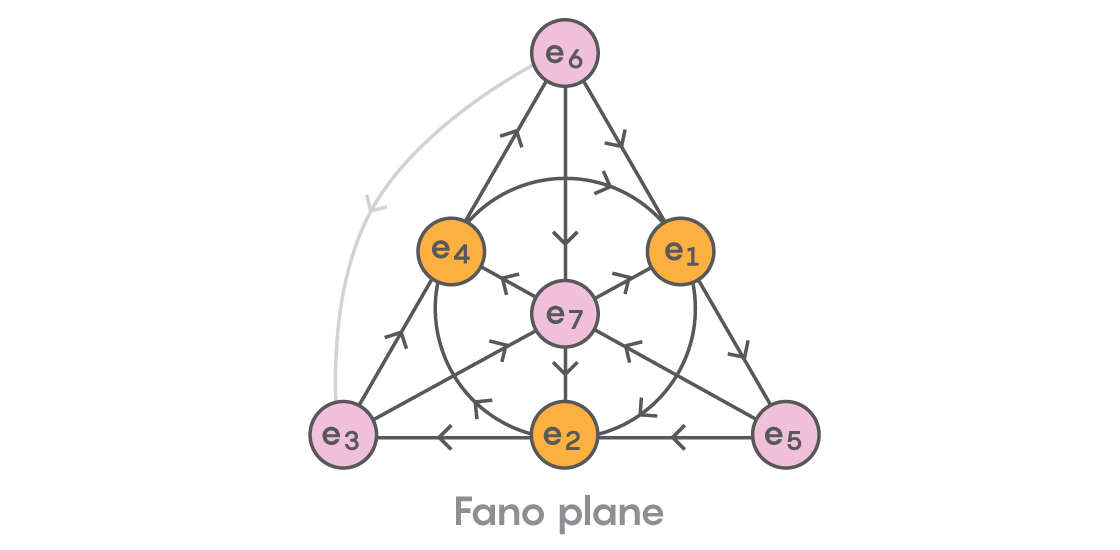
As in the representation for the quaternions, multiplying along the direction of the arrow gives a positive product, and against the arrow gives a negative one.

Like the quaternions, octonion multiplication is not commutative. But extending our idea of number out to the octonions costs us the associativity of multiplication as well. When multiplying three octonions x, y and z, it’s not necessarily true that (x × y) × z = x × (y × z). For example, using the diagram above, we can see that

$latex (e_{3}\times e_{4})\times e_{1}=e_{6}\times e_{1}=e_{5}$

but

$latex e_{3}\times(e_{4}\times e_{1})=e_{3}\times e_{2}=-e_{5}$

So now we have a number system with non-commutatitve, non-associative multiplication and seven square roots of -1. When would anyone ever use that? Well, some physicists believe that the octonions may hold the key to describing how the strong, weak and electromagnetic forces act on quarks, leptons and their anti-particles. If true, this could help resolve one of the great mysteries in modern physics.

By repeatedly extending the real numbers to create larger systems — the complex numbers, the quaternions, the octonions — in which we can add, subtract, multiply and divide, we lose a little familiarity with each step. Along the way, we may also lose touch with what we think of as real. But what we gain are new ways of thinking about the world. And we can always find a use for that.

Exercises

1. We created the complex numbers by defining i so that $latex i^2=-1$. Can you find a complex number z such that $latex z^2=i$?

Hint: Let z = a + bi and square it. Under what conditions on a and b would this be equal to i?

2. Let $latex z=\frac{1}{2}+\frac{\sqrt{3}}{2}i$. Show that $latex z^3=-1$. Can you find the other two cube roots of –1?

Download the “Four Special Number Systems” PDF graphic to share with students.

Correction added Oct. 26: William Rowan Hamilton’s middle name was misspelled as “Rohan” in the original post of this article.